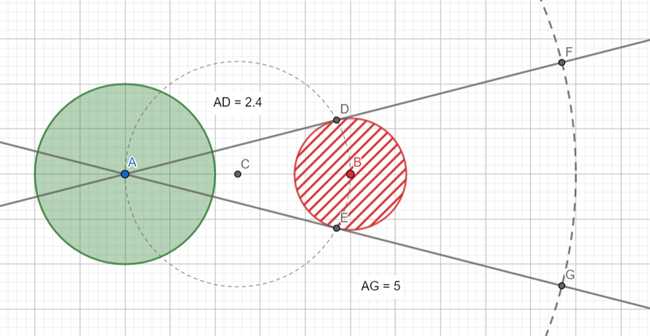
Когда мы имеем дело с двумя окружностями, имеющими разные радиусы и центры в точках С и D, одна из основных задач состоит в том, чтобы найти точки их пересечения. Это может быть полезно, например, при решении геометрических задач или при построении диаграмм. Точки пересечения окружностей E и F, в данном случае, являются точками, которые лежат одновременно и на окружности E и на окружности F. Поиск таких точек можно выполнить с помощью различных методов, используя геометрические принципы и формулы, такие как теорема Пифагора или уравнения окружности. В этой статье мы рассмотрим основные способы нахождения точек пересечения окружностей E и F с центрами в точках C и D.
Определение данных

Для решения данной задачи нам необходимо иметь следующие данные:
- Координаты центров окружностей C и D. Это необходимо для определения положения окружностей относительно друг друга и оси координат.
- Радиусы окружностей E и F. Радиусы позволяют определить расстояние от центров окружностей до их точек пересечения.
С помощью этих данных мы сможем определить точки пересечения окружностей E и F с центрами в точках C и D. Определение точек пересечения позволяет нам найти общие точки окружностей и понять, насколько они перекрываются друг с другом.
Для определения данных могут быть использованы различные методы и инструменты, такие как геометрические вычисления, аналитическая геометрия или программное обеспечение для работы с графиками и диаграммами. Важно иметь точность и достоверность данных, чтобы получить правильный результат.
Нахождение уравнений окружностей

Для нахождения уравнений окружностей с центрами в точках C и D, нам необходимо знать координаты этих точек и радиусы окружностей.
Уравнение окружности с центром в точке C и радиусом r записывается следующим образом:
(x — Cx)2 + (y — Cy)2 = r2
Где (Cx, Cy) — координаты центра окружности C, x и y — переменные координаты точек на плоскости, а r — радиус окружности.
При нахождении уравнения окружности с центром в точке D и радиусом R, мы заменяем C на D и r на R в уравнении выше:
(x — Dx)2 + (y — Dy)2 = R2
Зная координаты центров окружностей и их радиусы, мы можем составить систему уравнений, чтобы найти точки пересечения окружностей E и F.
Например, если у нас есть окружность E с центром в точке C1(2, 3) и радиусом r1 = 4, и окружность F с центром в точке C2(5, 7) и радиусом r2 = 3, мы можем записать следующую систему уравнений:
- (x — 2)2 + (y — 3)2 = 42
- (x — 5)2 + (y — 7)2 = 32
Решая эту систему уравнений, мы найдем значения x и y, которые будут являться координатами точек пересечения окружностей E и F. Эти точки будут удовлетворять обоим уравнениям системы.
Используя вышеприведенные формулы и методы, вы сможете легко найти уравнения окружностей и их точки пересечения. Уверены, что с помощью математики вы сможете справиться с этой задачей!
Нахождение точек пересечения окружностей E и F с центрами в точках C и D
Чтобы найти точки пересечения окружностей E и F с центрами в точках C и D, необходимо использовать геометрический метод и некоторые математические выкладки.
Для начала, давайте определимся с тем, что такое точка пересечения окружностей. Это точка, где линия пересечения двух окружностей пересекается с каждой из них. То есть, это точка, которая лежит одновременно на обеих окружностях. Искать точку пересечения окружностей можно аналитическими методами, используя уравнения окружностей.
Уравнение окружности E с центром в точке C можно записать следующим образом:
(x — Cx)^2 + (y — Cy)^2 = r1^2
- где (Cx, Cy) — координаты центра окружности C,
- r1 — радиус окружности E.
Аналогично, уравнение окружности F с центром в точке D имеет вид:
(x — Dx)^2 + (y — Dy)^2 = r2^2
- где (Dx, Dy) — координаты центра окружности D,
- r2 — радиус окружности F.
Теперь мы имеем два уравнения, и нам необходимо найти точки пересечения этих окружностей. Чтобы это сделать, решим систему уравнений, состоящую из уравнений окружностей E и F.
Результатом решения системы будут координаты точек пересечения окружностей. Используя эти координаты, можно определить физические координаты этих точек на плоскости.
Таким образом, ответ на вопрос о нахождении точек пересечения окружностей E и F с центрами в точках C и D состоит в решении системы уравнений окружностей E и F.
Проверка решения
Для проверки решения можно использовать различные методы. Один из них — графический метод. Нарисуйте на координатной плоскости окружности E и F с центрами в точках C и D. Затем отметьте найденные точки пересечения и убедитесь, что они действительно лежат на обеих окружностях.
Также можно математически проверить правильность решения. Для этого достаточно подставить координаты найденных точек пересечения в уравнения окружностей E и F и убедиться, что полученные значения равны.
Если оба метода подтверждают правильность решения, значит, точки пересечения окружностей E и F с центрами в точках C и D были найдены верно. В противном случае следует пересмотреть алгоритм решения или искать ошибку в процессе вычислений.






