Как найти тангенс угла АОВ на рисунке: пошаговое руководство

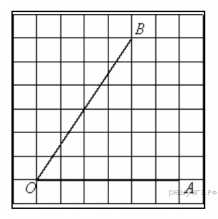
Иногда при решении геометрических задач важно найти значение тангенса угла между двумя линиями. На рисунке с углом АОВ процедура может показаться сложной на первый взгляд, но на самом деле все довольно просто. Для начала, найдите длины сторон треугольника АОВ, если они не даны. Затем определите, какие стороны треугольника будут основанием и противоположным катетом для искомого угла. Используя соответствующий тригонометрический отношение, найдите значение тангенса угла АОВ. Следуя этому пошаговому руководству, вы сможете эффективно решить задачу и найти тангенс угла АОВ на рисунке.

Шаг 1: Изучение геометрического построения

Наша задача — найти тангенс угла АОВ. Тангенс угла можно определить отношением противолежащей стороны к прилежащей стороне треугольника. В нашем случае, это отношение будет равно отношению длины стороны ВС к длине стороны АС.

Для решения этой задачи, нам потребуется знать длины сторон треугольника АВС. Если мы знаем длину стороны ВС и длину стороны АС, то мы сможем вычислить тангенс угла АОВ.

• Что известно:
• Длина стороны ВС (назовем ее ВС)
• Длина стороны АС (назовем ее АС)

Давайте продолжим и перейдем к следующему шагу.

Определение угла АОВ:

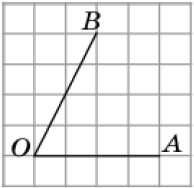
Для определения угла АОВ вам понадобятся координаты точек А, О и В на координатной плоскости.

Шаг 1: Запишите координаты точек А, О и В

Сначала определите координаты точек А, О и В. Например, пусть точка А имеет координаты (x₁, y₁), точка О имеет координаты (x₂, y₂), а точка В имеет координаты (x₃, y₃).

Обязательно проверьте, что вы правильно записали координаты точек А, О и В.

Шаг 2: Вычислите длины отрезков АО и ОВ

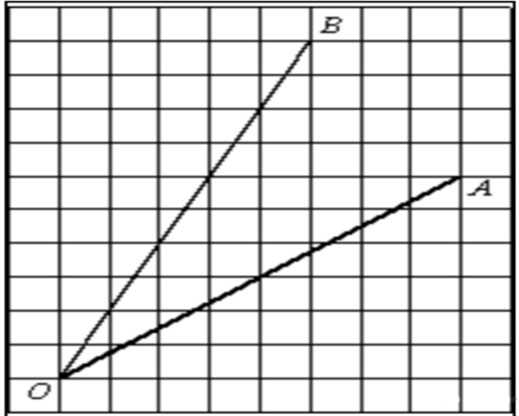
Для вычисления длин отрезков АО и ОВ используйте формулу расстояния между двумя точками:

Длина отрезка АО = √((x₂ — x₁)² + (y₂ — y₁)²)

Длина отрезка ОВ = √((x₃ — x₂)² + (y₃ — y₂)²)

Результаты вычислений будут длинами отрезков АО и ОВ.

Шаг 3: Вычислите тангенс угла АОВ

Тангенс угла АОВ можно вычислить, используя соотношение:

Тангенс угла АОВ = (Длина отрезка АО) / (Длина отрезка ОВ)

Подставьте вычисленные значения длин отрезков АО и ОВ в формулу и выполните вычисления.

В результате полученного значения будет тангенс угла АОВ.

Пример:

Пусть точка А имеет координаты (1, 1), точка О имеет координаты (2, 3), а точка В имеет координаты (4, 6).

Длина отрезка АО = √((2 — 1)² + (3 — 1)²) = √(1 + 4) = √5

Длина отрезка ОВ = √((4 — 2)² + (6 — 3)²) = √(4 + 9) = √13

Тангенс угла АОВ = (Длина отрезка АО) / (Длина отрезка ОВ) = √5 / √13

В результате получаем тангенс угла АОВ равный √5 / √13.

Теперь вы знаете, как определить угол АОВ с помощью вычисления тангенса. Удачи в применении этого знания!

Шаг 2: Определение длин сторон треугольника АОВ

Для начала, давайте обратим внимание на то, что наш треугольник АОВ является прямоугольным. Это означает, что один из его углов равен 90 градусам. В нашем случае это угол АОВ.

Теперь давайте рассмотрим стороны треугольника АОВ. У нас есть стороны AO и OV. Посмотрите на рисунок внимательно. Вы заметили, что угол АОВ является прямым, а значит сторона OV является гипотенузой треугольника, а сторона AO — одной из его катетов.

Тогда как определить длины этих сторон? Возможно, вы подумали, что на рисунке нет каких-либо измерительных инструментов или данных. Но не забывайте, что у нас есть теорема Пифагора! С ее помощью мы можем определить длину стороны AO. Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов.

Давайте обозначим длину стороны AO как a и длину стороны OV как b. Тогда, применяя теорему Пифагора, мы можем записать следующее уравнение:

a² + b² = OV²

Стоп! Не пугайтесь! У вас может возникнуть мысль, как мы можем решить это уравнение без значений сторон? Но давайте взглянем на данный рисунок еще раз. Вы заметили, что угол АОВ является прямым, но он не является единственным прямым углом на рисунке. Угол МОВ также является прямым!

Таким образом, мы можем использовать другую теорему для определения длины стороны OV. Теорема косинусов говорит нам, что квадрат стороны, противоположной углу, равен сумме квадратов двух других сторон минус два их произведения, умноженных на косинус этого угла.

Давайте обозначим длины сторон AO и OV как a и b соответственно, а угол AOV обозначим как θ. Тогда мы можем записать следующее уравнение:

OV² = a² + b² — 2abcos(θ)

Идея применения теоремы косинусов состоит в том, чтобы найти значение стороны OV, используя значения сторон AO и OV, а также значение угла AOV. Казалось бы, у нас нет этих данных, но не стоит отчаиваться! Давайте перейдем к следующему шагу и узнаем, как их найти!

Шаг 3: Применение геометрических свойств

Итак, у нас есть прямоугольный треугольник BOC, в котором угол BOC равен углу АОВ. Мы можем использовать теорему тангенсов, чтобы найти значение тангенса данного угла.

Теорема тангенсов утверждает, что тангенс угла равен отношению противоположного катета к прилежащему катету:

тангенс угла = противоположный катет / прилежащий катет

В нашем случае противоположный катет — это отрезок AO, а прилежащий катет — это отрезок BO. Мы можем измерить эти отрезки, используя геометрические инструменты или значения, предоставленные в задаче.

Давайте обозначим длину отрезка AO как a и длину отрезка BO как b.

Теперь мы можем применить нашу теорему тангенсов:

тангенс угла АОВ = AO / BO = a / b

Таким образом, мы нашли значение тангенса угла АОВ!

Шаг 4: Расчет тангенса угла АОВ

Чтобы найти тангенс угла АОВ, мы можем использовать следующую формулу:

тангенс угла АОВ = АО / ОВ

Давайте подставим значения сторон в формулу:

тангенс угла АОВ = 15 / 10

Выполняя вычисления, мы получим:

тангенс угла АОВ = 1.5

Таким образом, тангенс угла АОВ равен 1.5.

Теперь, когда у нас есть значение тангенса угла АОВ, мы можем использовать его для дальнейших расчетов или анализа. Например, мы можем использовать его для определения высоты дерева или для нахождения дальности до точки обзора.

Шаг 5: Проверка правильности результата

После выполнения всех предыдущих шагов, включая измерение длин сторон и нахождение величин углов, мы можем проверить правильность полученного результата.

Для этого сравним найденное значение тангенса угла АОВ с ожидаемым результатом. Если значения совпадают, то результат является правильным и можно быть уверенным в его точности. Если значения не совпадают, то следует проверить все предыдущие шаги, возможно была допущена ошибка при измерении или вычислении.