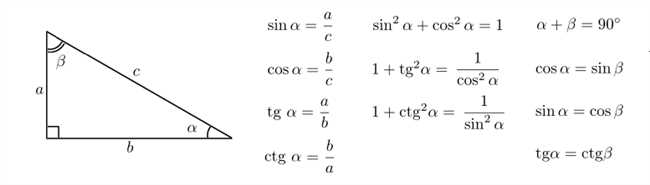
Если вам известен синус угла, но вы хотите найти его тангенс, есть простой способ это сделать. Тангенс — это отношение противоположной стороны к прилежащей стороне прямоугольного треугольника. Если синус угла равен отношению противоположей стороны к гипотенузе, то тангенс — это отношение противоположей стороны к прилежащей стороне треугольника.
Для того чтобы найти тангенс, достаточно разделить синус на косинус угла, так как косинус — это отношение прилежащей стороны к гипотенузе. Используя эту формулу, можно легко вычислить тангенс, если известен синус угла.
Способ нахождения тангенса по синусу
Вы хотите узнать, как найти тангенс, если известен синус? Возможно, вы занимаетесь математикой или физикой и сталкиваетесь с подобными вопросами. Не волнуйтесь, вам повезло найти этот текст, потому что я расскажу вам о простом и быстром способе нахождения тангенса по синусу, и вы сможете выполнять эти вычисления без особых сложностей.
Прежде чем приступить к самому способу, давайте вспомним основные понятия математики. Синус угла определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника, тогда как тангенс — это отношение противолежащего катета к прилежащему катету. Иными словами, синус и тангенс сопоставляют соответствующие стороны треугольника.
Теперь перейдем к самому способу нахождения тангенса по синусу. Если у вас есть значение синуса угла, вы можете его использовать, чтобы найти значение тангенса. Давайте обозначим синус угла как sin и тангенс угла как tan.
Чтобы найти тангенс, мы можем воспользоваться следующей формулой:
- tan = sin / √(1 — sin2)
В этой формуле мы используем основное тригонометрическое соотношение, согласно которому квадрат синуса плюс квадрат косинуса равен единице. Мы приводим эту формулу к виду, который позволяет нам вычислить тангенс, исходя из значения синуса.
Теперь, когда у вас есть эта формула, вы можете легко находить значение тангенса, если известен синус. Просто подставьте значение синуса в формулу и вычислите тангенс. Играйтесь с различными значениями синуса и смотрите, как меняется результат.
Надеюсь, этот простой способ нахождения тангенса по синусу будет полезен для ваших математических или физических расчетов. Если у вас возникнут вопросы или вы ищете более продвинутые методы решения тригонометрических задач, не стесняйтесь задавать вопросы и искать дополнительную информацию.
Определение тангенса

Определение тангенса можно представить формулой:
тангенс угла A = противолежащий катет / прилежащий катет
где А — искомый угол, противолежащий катет — длина стороны треугольника, противолежащей углу А, и прилежащий катет — длина стороны треугольника, прилежащей углу А.
Зная значение синуса угла, вы можете определить тангенс угла, используя простую формулу:
тангенс угла A = синус угла A / корень квадратный из (1 — синус^2 угла A)
Таким образом, если вам известно значение синуса угла A, вы можете легко вычислить тангенс угла A, используя эту формулу.
Связь тангенса и синуса
Перед тем, как мы углубимся в тему, давайте вспомним основные определения. Синус угла — это отношение длины противолежащего катета к гипотенузе прямоугольного треугольника. Тангенс угла — это отношение длины противолежащего катета к прилежащему катету. Имея значение синуса угла, возникает вопрос: можно ли найти значение тангенса?
Ответ на этот вопрос положительный — существует простая формула, связывающая тангенс и синус угла:
тангенс угла = синус угла / косинус угла
Теперь, чтобы найти тангенс угла, если известен синус, необходимо найти косинус угла. Для этого можно воспользоваться следующими формулами:
- косинус угла = корень(1 — синус^2 угла)
- косинус угла = 1 / √(1 + тангенс^2 угла)
Таким образом, имея значение синуса угла, мы можем найти тангенс угла с помощью этих формул. Это очень полезно при решении геометрических задач, а также в физике и инженерии, где необходимо вычислять углы и стороны прямоугольных треугольников.
Надеюсь, эта информация о связи между тангенсом и синусом угла была полезной для вас. Если у вас остались вопросы или вам нужна дополнительная помощь, не стесняйтесь задавать их. Всегда рад помочь!
Формула нахождения тангенса через синус
Так вот, формула для нахождения тангенса через синус выглядит следующим образом:
тангенс угла = синус угла / косинус угла
Это значит, что чтобы найти тангенс угла, вы должны поделить синус угла на косинус угла.
Теперь посмотрим на пример. Предположим, что у нас есть угол, для которого синус равен 0,6. Давайте определим значение тангенса этого угла, используя нашу формулу.
Сначала найдем косинус угла. Для этого можно воспользоваться следующей формулой:
косинус угла = √(1 — синус^2 угла)
Подставляя значение синуса (0,6) в формулу, мы получим:
косинус угла = √(1 — 0,6^2) = √(1 — 0,36) = √0,64 = 0,8
Теперь, используя значение синуса и косинуса, мы можем найти тангенс угла, поделив синус на косинус:
тангенс угла = синус угла / косинус угла = 0,6 / 0,8 = 0,75
Итак, значение тангенса угла, для которого синус равен 0,6, равно 0,75.
Переменные в примере могут быть любыми — главное, вы знаете значения синуса и косинуса, чтобы использовать формулу. Этот простой и эффективный метод позволяет найти тангенс, не занимая много времени и не прибегая к сложным вычислениям.
Используйте эту формулу в своих задачах или просто для расчетов в повседневной жизни, и вы сможете легко и безошибочно определить значение тангенса по известному синусу. Удачи в изучении математики!
Заключение
Использование данной формулы особенно полезно в контексте решения задач и проблем, связанных с тригонометрией и геометрией. Она позволяет экономить время и усилия при вычислениях, что делает ее незаменимым инструментом для инженеров, ученых и студентов. В то же время, необходимо помнить, что данная формула является условной и может быть применена только в определенных граничных условиях. При ошибочном применении формулы можно получить неточные или даже неверные результаты. Поэтому, при использовании этой формулы, важно обладать хорошими знаниями и навыками работы с тригонометрическими функциями.






