Когда мы знаем длину диагонали квадрата, нам может быть интересно узнать значения его сторон. Это может быть полезно, например, для построения квадрата или решения геометрических задач. В этой статье я расскажу, как найти стороны квадрата через диагональ. Есть несколько способов решения этой задачи. Наиболее простым и распространенным является использование формулы, которая основана на теореме Пифагора. Пользуясь этой формулой, мы можем найти сторону квадрата, зная длину его диагонали. Также, я расскажу о другом методе, который основан на свойствах равнобедренного треугольника. Давайте разберемся, как это работает.
Определение диагонали квадрата и ее связь со сторонами
Связь между диагональю квадрата и его сторонами может быть выражена с помощью формулы, которая позволяет найти длину стороны квадрата, если известна его диагональ:
- Длина стороны квадрата (a) равна длине диагонали (d) разделенной на корень из двух (√2):
a = d / √2
Эта формула гарантирует, что диагональ квадрата и его стороны связаны друг с другом и зависят от одного и того же параметра — длины диагонали. Она позволяет нам вычислить значение стороны квадрата, если известна его диагональ, или наоборот, найти длину диагонали, если известна сторона квадрата.
Если, например, мы знаем длину диагонали квадрата и хотим найти длину его стороны, то мы можем использовать данную формулу. Просто подставляем известное значение диагонали (d) в формулу и вычисляем длину стороны (a).
Таким образом, диагональ квадрата и его стороны взаимосвязаны и могут быть рассчитаны с использованием простой математической формулы. Это помогает нам легко определить размеры квадрата, исходя из известной диагонали, или наоборот, найти диагональ, если известна длина стороны.
Применение теоремы Пифагора для нахождения сторон квадрата
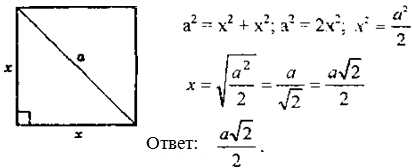
Используя теорему Пифагора, можно легко найти стороны квадрата через его диагональ. Давайте рассмотрим, как это можно сделать.
Предположим, что у нас есть квадрат со стороной x и диагональю d. Мы хотим найти значение x. Для этого мы можем использовать теорему Пифагора для прямоугольного треугольника, образованного диагональю квадрата и его сторонами. Длина гипотенузы этого треугольника равна d, а длины катетов — x.
Используя теорему Пифагора, мы можем записать уравнение:
x^2 + x^2 = d^2
Сокращая эту запись, получим:
2x^2 = d^2
Теперь, чтобы найти значение x, нам нужно решить это уравнение. Для этого мы можем применить обратные операции. Сначала разделим обе части уравнения на 2:
x^2 = d^2 / 2
Затем извлечем квадратный корень из обоих частей уравнения:
x = √(d^2 / 2)
Таким образом, мы получаем выражение для нахождения стороны квадрата через его диагональ:
x = √(d^2 / 2)
Теперь у нас есть формула, которую мы можем использовать для решения задач, связанных с нахождением сторон квадрата через его диагональ.
Применение теоремы Пифагора для нахождения сторон квадрата может быть полезно, например, при расчетах в строительстве или при решении геометрических задач. Это простой и эффективный метод, который позволяет найти значения сторон квадрата с помощью диагонали.
Использование формулы для нахождения сторон квадрата через диагональ
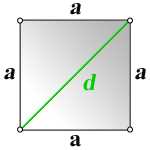
Если у вас есть квадрат, и вам нужно найти длину его сторон, зная только длину диагонали, существует простая формула, которая позволит вам это сделать. Давайте разберемся, как это работает.
Формула, которую нужно использовать, основана на теореме Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В нашем случае гипотенуза является диагональю квадрата, а катеты — стороны квадрата. Итак, формула для нахождения сторон квадрата через диагональ будет выглядеть следующим образом:
Сторона = Диагональ / √2
Для того, чтобы использовать эту формулу, вам достаточно знать только длину диагонали. Просто подставьте значение диагонали в формулу и выполните соответствующие вычисления.
Например, предположим, что у вас есть квадрат с диагональю длиной 10 см. Чтобы найти длину каждой стороны этого квадрата, вы можете использовать формулу:
Сторона = 10 / √2 ≈ 7.07 см
Таким образом, сторона квадрата будет примерно равна 7.07 см.
Используя эту формулу, вы можете легко и точно определить длину сторон квадрата, имея только информацию о его диагонали. Это очень полезно в различных практических ситуациях, например, при строительстве или проектировании.
Примеры расчета сторон квадрата через диагональ
Выше было объяснено, как найти стороны квадрата через диагональ с помощью формулы:
a = d / √2
где a — длина каждой стороны квадрата, а d — длина диагонали.
Для лучшего понимания применения этой формулы предлагаем рассмотреть несколько примеров:
-
Пример 1: Диагональ квадрата равна 10 см. Какова длина каждой стороны квадрата?
Для расчета подставим значение диагонали d = 10 в формулу a = d / √2:
a = 10 / √2 ≈ 7.07
Таким образом, длина каждой стороны квадрата составляет примерно 7.07 см.
-
Пример 2: Диагональ квадрата равна 5 м. Какова длина каждой стороны квадрата?
Аналогично, подставим значение d = 5 в формулу a = d / √2:
a = 5 / √2 ≈ 3.54
Таким образом, длина каждой стороны квадрата составляет примерно 3.54 м.
Таким образом, для расчета сторон квадрата через его диагональ необходимо использовать формулу a = d / √2, где a — длина каждой стороны, а d — длина диагонали. Это позволяет легко и быстро определить размеры квадрата, когда известна только длина его диагонали.






