Методы вычисления стороны треугольника

1. Использование теоремы Пифагора. Если известны две стороны треугольника и необходимо найти третью сторону, можно использовать теорему Пифагора. Согласно этой теореме, квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов. Таким образом, зная длины двух сторон треугольника, можно найти длину третьей стороны.
2. Использование тригонометрических функций. Если известны длины одной стороны треугольника и двух прилежащих к ней углов, можно использовать тригонометрические функции (синус, косинус или тангенс) для вычисления длины другой стороны. Например, если известны длина одной стороны и мера ее противолежащего угла, можно использовать синус или косинус для нахождения длины другой стороны.
3. Использование формулы для нахождения высоты треугольника. Если известны длины сторон треугольника и необходимо найти длину третьей стороны, можно использовать формулу для нахождения высоты треугольника. Если треугольник не является прямоугольным, можно использовать формулу полупериметра и радиуса вписанной окружности для нахождения длины стороны.
4. Использование теоремы косинусов. Если известны длины двух сторон треугольника и мера угла между ними, можно использовать теорему косинусов для вычисления длины третьей стороны. Согласно этой теореме, квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус между ними.
5. Использование теоремы синусов. Если известны длины двух сторон треугольника и меры угла, образованного этими сторонами, можно использовать теорему синусов для вычисления длины третьей стороны. Согласно этой теореме, отношение синуса меры угла к длине стороны треугольника равно отношению синуса меры угла, образованного другими двумя сторонами, к их сумме.
Теорема Пифагора
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза — это наибольшая сторона треугольника, которая расположена напротив прямого угла. А катеты — это две меньшие стороны треугольника, которые образуют прямой угол.
Помнишь, что такое квадрат числа? Квадрат числа — это само число, умноженное на себя. Например, квадрат числа 3 равен 3 * 3 = 9.
Давай рассмотрим простой пример, чтобы лучше понять, как работает теорема Пифагора.
Пример:
У нас есть прямоугольный треугольник со сторонами 3 и 4. Мы хотим найти длину гипотенузы.
Сначала нужно квадрат каждой из сторон и найти их сумму:
- Квадрат стороны 3: 3 * 3 = 9
- Квадрат стороны 4: 4 * 4 = 16
Теперь сложим их: 9 + 16 = 25
Полученная сумма — это квадрат гипотенузы. Чтобы найти саму гипотенузу, нужно извлечь из этого числа квадратный корень:
Корень квадратный из 25 равен 5.
Таким образом, длина гипотенузы в нашем примере равна 5.
Ты видишь, как просто работать с теоремой Пифагора? Это несложное и эффективное правило, которое позволяет нам находить стороны прямоугольных треугольников, только зная длины остальных сторон.
Теперь, когда ты разобрался в основах Теоремы Пифагора, ты можешь использовать ее, чтобы решать задачи на нахождение сторон треугольников. Уверен, что ты справишься!
Закон синусов
Одним из основных принципов закона синусов является отношение длины стороны к синусу противолежащего ей угла. Более точно, закон синусов гласит:
Отношение длин сторон треугольника к синусам соответствующих углов одинаково и равно отношению радиуса описанной окружности к диаметру:
а/sin(A) = b/sin(B) = c/sin(C) = 2R,
где a, b, c — длины сторон треугольника,
A, B, C — соответственные им углы,
R — радиус описанной окружности.
Теперь, когда мы знакомы с формулой закона синусов, давайте рассмотрим пример его применения для нахождения неизвестной стороны треугольника.
Пример
Представьте, что у нас есть треугольник со сторонами длиной 5 и 7, и между ними угол в 60 градусов. Мы хотим найти длину третьей стороны треугольника.
Используя закон синусов, мы можем записать:
5/sin(60) = c/sin(C).
Мы знаем, что синус 60 градусов равен √3/2, поэтому у нас есть:
5/(√3/2) = c/sin(C).
Сокращая, мы получаем:
10/√3 = c/sin(C).
Используя тригонометрическую таблицу или калькулятор, мы можем найти, что синус угла C составляет примерно 0,866. Теперь мы можем решить уравнение:
10/√3 = c/0.866.
Перемножим обе стороны уравнения:
c = (10/√3) * 0.866 ≈ 8.660254.
Таким образом, длина третьей стороны треугольника примерно равна 8.660254.
Вот и все! Теперь вы знакомы с законом синусов и можете использовать его для нахождения неизвестной стороны треугольника при известных сторонах и углах. Уверен, что эти знания пригодятся вам как в учебе, так и в повседневной жизни. Удачного применения!
Закон косинусов
Закон косинусов формулируется следующим образом: квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Математический вид формулы закона косинусов:
c² = a² + b² — 2ab*cos(C)
Где:
- c — длина стороны, которую мы хотим найти
- a и b — длины известных сторон треугольника
- C — угол между известными сторонами
Используя эту формулу, мы можем вычислить длину третьей стороны треугольника, если известны длины двух других сторон и угол между ними.
Давайте рассмотрим пример:
У нас есть треугольник, у которого известны стороны a = 6 и b = 8, а угол между ними C = 45°. Чтобы найти длину третьей стороны c, мы будем использовать закон косинусов.
Применим формулу закона косинусов:
c² = 6² + 8² — 2 * 6 * 8 * cos(45°)
c² = 36 + 64 — 96 * cos(45°)
c² = 100 — 96 * cos(45°)
Теперь посчитаем длину третьей стороны c:
c = √(100 — 96 * cos(45°))
c ≈ 2.83
Таким образом, длина третьей стороны треугольника составляет примерно 2.83.
Закон косинусов является полезным инструментом для вычисления сторон треугольника, особенно когда известны только длины сторон и углы между ними. Он позволяет нам решать различные задачи, связанные с построением и измерением треугольников.
Примеры расчета стороны треугольника
Вот несколько примеров расчета стороны треугольника:
1. Использование теоремы Пифагора
Если у нас есть прямоугольный треугольник, то мы можем использовать теорему Пифагора, чтобы найти длину его стороны. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов двух катетов. Например, если у нас есть треугольник со сторонами 3 и 4, мы можем найти длину гипотенузы, используя следующую формулу:
c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5.
2. Использование тригонометрических функций
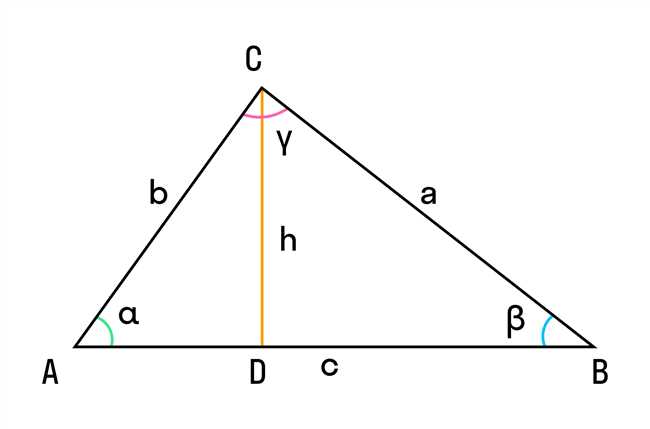
В случае, когда треугольник не является прямоугольным, мы можем использовать тригонометрию для определения длины его сторон. Например, если у нас есть треугольник с углом α и известной длиной стороны a, можно использовать функцию синуса для расчета длины противолежащей стороны b:
b = a * sin(α).
Точно так же можно использовать функции косинуса и тангенса, чтобы найти длины других сторон треугольника.
3. Использование формулы полупериметра
Другой метод для расчета длины сторон треугольника — использование формулы полупериметра. Полупериметр треугольника — это половина суммы его сторон. Если у нас есть треугольник со сторонами a, b и c, то его полупериметр вычисляется следующим образом:
s = (a + b + c) / 2.
Затем можно использовать формулу Герона для расчета площади треугольника и длины его сторон:
Area = √(s(s — a)(s — b)(s — c)).
С помощью этой формулы можно найти длины всех сторон треугольника.
Таким образом, существует много способов нахождения сторон треугольника. Важно знать основные принципы и формулы, чтобы успешно решать задачи и находить нужные значения.
Пример 1: Вычисление стороны по теореме Пифагора
Для примера возьмем треугольник со сторонами a = 3 и b = 4. Используя теорему Пифагора, мы можем вычислить длину гипотенузы (c) следующим образом:
1. Поставьте уравнение по теореме Пифагора:
c² = a² + b²
2. Подставьте значения:
c² = 3² + 4² = 9 + 16 = 25
3. Вычислите квадратный корень для обеих сторон уравнения:
c = √25 = 5
Таким образом, длина третьей стороны треугольника равна 5.






