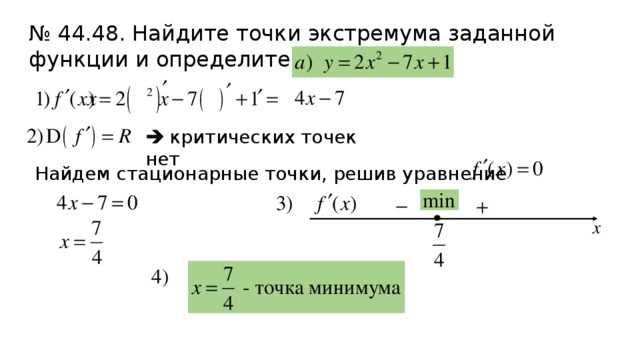
Когда мы рассматриваем функцию, нам часто приходится находить ее стационарные точки или точки экстремума. Стационарная точка — это точка на графике функции, где ее производная равна нулю. Найти стационарные точки может быть сложной задачей, особенно если функция имеет сложную формулу или состоит из нескольких частей. Однако, существуют различные методы и советы, которые могут помочь нам найти эти точки. Некоторые из них включают использование производной функции, решение уравнений, анализ поведения функции на интервалах и применение численных методов. В этой статье мы рассмотрим несколько методов и дадим советы, которые помогут нам найти стационарные точки функции.
Стационарные точки: советы и методы
Один из способов найти стационарные точки — это приравнять производную функции к нулю и решить полученное уравнение. Если при таком подходе нахотятся все корни уравнения производной, то эти точки будут являться стационарными. Однако, это не единственный метод и некоторые функции могут не иметь производной.
Следующий подход для нахождения стационарных точек — использование градиента функции. Градиент — это вектор, указывающий направление наибольшего изменения функции. Когда градиент равен нулю, это означает, что функция достигает локального минимума, максимума или седловой точки.
Также можно использовать методы оптимизации, такие как генетические алгоритмы, методы частиц и эволюционные стратегии, чтобы найти стационарные точки функции. Эти методы используют итерационные процессы и пробуют различные значения аргументов, чтобы найти наилучшее решение.
Еще один подход — это графическое представление функции и поиск точек экстремума на графике. Это может быть полезным для функций с непрерывной производной, где экстремальные точки будут соответствовать стационарным.
В целом, нахождение стационарных точек требует тщательного анализа функции и использования различных методов. Некоторые точки могут быть легко найдены, в то время как другие могут требовать более сложных методов и алгоритмов. Важно помнить, что не всегда существует единственное решение, и иногда может потребоваться итеративный подход для достижения оптимального результата.
Что такое стационарные точки?
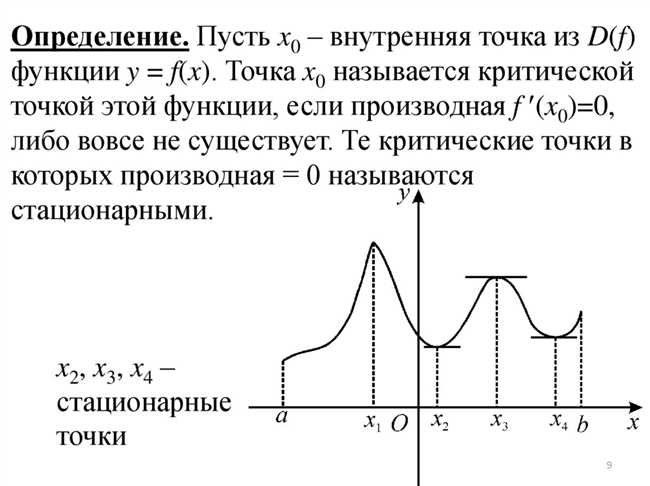
Прежде чем мы погрузимся в детали, давайте представим, что вы идете по горному маршруту. Во время вашего путешествия вы можете натолкнуться на некоторые точки, где вы чувствуете постоянство, где путь кажется прямым и горизонтальным. В мире математики эти точки называются стационарными точками.
Представьте, что вы пришли к красивой водопадной реке и решили подняться в гору, чтобы получить наилучший вид на эту удивительную природную красоту. На протяжении вашего подъема вы можете заметить, что некоторые точки выделяются. Они представляют собой места, где вы приостанавливаетесь и наслаждаетесь обстановкой. Это то, что называется стационарной точкой — точкой, в которой производная функции равна нулю или не существует.
Стационарные точки имеют особое значение в математике, они являются ключевыми моментами в изучении функций, так как они могут помочь нам найти экстремумы функции или определить поведение функции вблизи этих точек. Стационарные точки находят свое применение в различных областях, таких как оптимизация, физика и экономика.
Итак, как мы можем найти стационарные точки? Один из способов — это найти производную функции и найти значения переменной, при которых эта производная равна нулю или не существует. Это позволит нам определить стационарные точки функции.
Другой способ — это построение графика функции и анализ ее поведения вблизи точек, где график касается горизонтальной линии или имеет точек перегиба.
Вот несколько вопросов для размышления: какую роль играют стационарные точки в оптимизации? Почему стационарные точки важны для физики и экономики? Как можно использовать стационарные точки для определения поведения функции вблизи этих точек? Размышляйте и исследуйте мир стационарных точек!
Зачем искать стационарные точки?

Друг мой, что может быть более захватывающим, чем путешествие к неизведанным вершинам? Помнишь, как Магеллан обогнал Землю или Хиллари покорил Эверест? Такими же исследователями мы можем стать и в мире науки, когда начинаем искать стационарные точки. Но что такое стационарные точки и зачем их искать?
Стационарные точки — это точки в функции, где производная равна нулю. Если представить функцию как гору, то стационарные точки будут вершинами или ямами на этой горе. Но почему их нужно искать? Позволь мне рассказать тебе об этом.
Первое и самое очевидное преимущество поиска стационарных точек — это нахождение экстремумов функции. Кто не хочет найти самую высокую гору или самую глубокую яму? Найдя стационарные точки, мы можем определить значения функции в этих точках и найти наибольшее и наименьшее значение функции на заданном интервале. Это может пригодиться, например, при оптимизации бизнес-процессов или разработке новых продуктов.
Если ты обратил внимание, то возможно заметил, что я упоминал, что стационарными точками могут быть как вершины, так и ямы. Так вот, второе важное применение стационарных точек заключается в нахождении точек перегиба функции. Это места, где функция меняет свой выпуклый или вогнутый характер. Понимание точек перегиба позволяет нам более глубоко изучить поведение функции и принять более обоснованные решения.
Кто не ищет, тот не находит, верно? В поисках стационарных точек мы обретаем не только знание, но и удовлетворение от разгадывания загадки функции. Как головоломки или гонки на выживание, поиск стационарных точек заставляет нас использовать все свои знания, интеллект и терпение, чтобы найти эту волшебную развилку, где функция изменяет свое поведение.
Но, возможно, самое важное в поиске стационарных точек — это возможность сделать себе исключительное дело. Между нами говоря, ведь нам всем хочется оставить свой след в истории. Решив задачу по поиску стационарных точек, мы можем чувствовать себя настоящими пионерами в науке. Пожалуй, начнем искать стационарные точки не только ради них самих, но и ради нас самих. Ведь наше путешествие находится только в начале, и эти точки лишь одна из многих загадок, которые нам предстоит разгадать.
Методы поиска стационарных точек
1. Аналитический метод
Аналитический метод основан на анализе производной функции и её равенства нулю. Этот метод широко используется в математике и физике для нахождения стационарных точек. Он позволяет найти точное значение точек, где производная функции равна нулю. Однако, применение аналитического метода может быть сложным и требует математической экспертизы.
2. Итерационный метод
Итерационный метод является численным методом решения задачи о стационарных точках. Он основан на последовательных приближениях итераций, где каждое новое приближение берется как функция предыдущего приближения. Этот метод находит приближенное значение стационарной точки, а не точное значение. Часто итерационные методы используются в компьютерных приложениях для численного решения задач.
3. Графический метод
Графический метод основан на построении графика функции и визуальном анализе его поведения. При помощи графического метода можно найти приблизительные значения стационарных точек. Для этого необходимо найти точки, где график функции пересекает ось абсцисс или имеет вершины. Хотя графический метод не дает точных значений стационарных точек, он может быть полезным в начальной стадии анализа.
4. Численные методы
Численные методы основаны на алгоритмах численного приближения и решения уравнений. Они широко применяются в компьютерной математике и имеют различные подходы для нахождения стационарных точек. Некоторые из этих методов включают метод Ньютона, метод золотого сечения и метод половинного деления. Численные методы обладают высокой точностью и эффективностью, но требуют использования компьютерных программ или приложений.
В зависимости от сложности функции и требуемой точности, можно выбрать наиболее подходящий метод для поиска стационарных точек. Часто при решении прикладных задач используются комбинации различных методов, чтобы получить наиболее точный и полный результат.
Как использовать стационарные точки?

1. Самоанализ и интроспекция: Одним из способов использования стационарных точек является использование их для самоанализа и интроспекции. Создайте тихое пространство, где вы можете погрузиться в свои мысли и осознать, что вам действительно важно и чего вы хотите достичь. Рассмотрите свои цели и планы для будущего, а также определите, что для вас на самом деле важно.
2. Проекты и планирование: Стационарные точки также полезны при разработке проектов и планировании. Они могут использоваться как отправная точка для определения этапов, ресурсов и временных рамок, необходимых для успешной реализации проекта. Определите, какие стационарные точки могут вам помочь определить ключевые моменты в процессе выполнения задачи или достижения цели.
3. Распределение времени и приоритизация: Когда у вас много задач и обязанностей, стационарные точки могут быть полезны для распределения времени и приоритизации. Идентифицируйте, какие задачи или обязанности являются наиболее важными, и создайте стационарные точки, чтобы убедиться, что вы отводите достаточно времени для их выполнения. Можете использовать таблицу с приоритетами, чтобы прояснить порядок выполнения задач.
4. Развитие навыков и личностного роста: Стационарные точки можно использовать для развития навыков и достижения личного роста. Определите области, в которых вы хотите улучшиться, и создайте стационарные точки, чтобы оценить свой прогресс и достижения. Например, если вы хотите стать более эффективным руководителем, установите стационарную точку для оценки своей коммуникации, управления временем и эмоционального интеллекта.
5. Отдых и восстановление: Как источники стабильности, стационарные точки могут использоваться для отдыха и восстановления. Найдите места или время, где вы можете ощутить покой и спокойствие, и создайте стационарные точки, чтобы регулярно отдыхать и заряжаться энергией. Это может быть утренняя прогулка в парке или время, проведенное в спа-салоне.
В итоге, стационарные точки представляют собой мощный инструмент для самоанализа, планирования, приоритизации, развития навыков и отдыха. Они могут помочь вам разобраться в своих целях и стратегиях, а также дать вам определенность и уверенность в течение вашего пути к успеху. Не бойтесь использовать стационарные точки, чтобы создать стабильную основу для своего роста и достижений.
Практические советы по поиску и использованию стационарных точек
В поиске и использовании стационарных точек есть несколько полезных советов:
- Анализ первой и второй производных: Для определения стационарных точек нужно проанализировать первую и вторую производные функции. Первая производная равна нулю в точках экстремума, в то время как вторая производная позволяет определить тип экстремума (максимум или минимум).
- Графический анализ: Использование графиков функции поможет наглядно определить точки, в которых производная равна нулю. График функции, пересекающий ось абсцисс приращается о стационарной точке, а его выпуклость помогает оценить тип экстремума.
- Методы численного решения: Для сложных функций, аналитическое нахождение стационарных точек может быть затруднено. В таких случаях можно использовать численные методы, такие как метод Ньютона, метод золотого сечения или метод дихотомии, чтобы приближенно найти эти точки.
Стационарные точки являются важным инструментом в анализе и оптимизации функций. Их поиск и использование помогает определить экстремумы функции и определить её поведение в различных точках. Используйте эти практические советы и методы для успешной работы с стационарными точками.






