Когда мы знаем косинус угла, а нужно найти его синус, мы можем использовать несколько простых способов. Это полезно, когда точных значений синуса угла нет в таблицах или калькуляторах. Одним из способов является использование тригонометрической формулы, связывающей синус и косинус угла. Еще один способ — использование пифагоровой теоремы для нахождения третьей стороны прямоугольного треугольника, а затем вычисление синуса угла. Также, зная косинус и значение самого угла, можно воспользоваться известной формулой, связывающей синус и косинус этого угла. В этой статье мы рассмотрим все эти способы более подробно и покажем, как их применять на практике.
Использование тригонометрической формулы
Для нахождения синуса угла по известному косинусу применяется следующая формула: синус угла равен квадратному корню из 1 минус квадрат косинуса угла. Это выражение легко запомнить и использовать в разных ситуациях.
Давайте рассмотрим пример для более ясного понимания. Предположим, что нам известно значение косинуса угла и мы хотим найти его синус. Пусть косинус угла равен 0.6. Тогда, используя формулу, мы получаем:
- Синус угла = √(1 — 0.6^2)
- Синус угла = √(1 — 0.36)
- Синус угла = √0.64
- Синус угла ≈ 0.8
Таким образом, синус угла составляет около 0.8.
Тригонометрическая формула является одним из простых способов нахождения синуса угла, если известен его косинус. Это полезное математическое соотношение, которое может быть использовано для решения различных задач и проблем.
Теперь, когда вы знакомы с использованием тригонометрической формулы для нахождения синуса угла по известному косинусу, вы можете применить этот инструмент в своих математических расчетах и решениях.
Использование геометрических соотношений
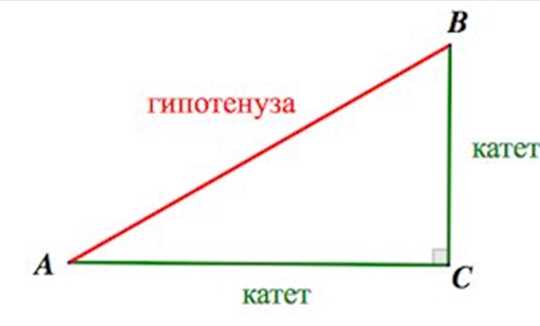
Часто, при решении математических задач, мы можем использовать геометрические соотношения для нахождения нужных нам значений. Найдем синус угла, если нам дан косинус. Для этого нам понадобятся следующие геометрические соотношения:
- Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
- Определение косинуса: косинус угла в прямоугольном треугольнике равен отношению длины прилежащего катета к гипотенузе.
- Определение синуса: синус угла в прямоугольном треугольнике равен отношению длины противоположенного катета к гипотенузе.
Итак, у нас есть задача найти синус угла, зная косинус. Вспомним определение косинуса: косинус угла равен отношению длины прилежащего катета к гипотенузе. Таким образом, если мы знаем косинус, мы можем найти отношение длин катета к гипотенузе.
Далее, воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Зная отношение длин катета к гипотенузе, мы можем найти длину гипотенузы.
Таким образом, имея длину гипотенузы и противоположенного катета, мы можем найти синус угла с помощью определения синуса: синус угла равен отношению длины противоположенного катета к гипотенузе.
В итоге, мы использовали геометрические соотношения (теорему Пифагора и определение синуса и косинуса) для нахождения синуса угла, зная косинус. Этот метод позволяет нам решать такие задачи и вычислять неизвестные значения с использованием геометрической информации.
Использование таблиц синусов и косинусов
Когда речь идет о поиске синуса угла, зная косинус, стоит обратить внимание на возможность использования таблиц синусов и косинусов. Такие таблицы могут быть очень полезными в процессе решения задач и упрощения вычислений.
В таблице синусов и косинусов указаны значения этих функций для различных углов. С помощью таблицы можно быстро найти синус и косинус угла, зная его значение косинуса. Достаточно найти в таблице значение косинуса, близкое к известному, а затем прочитать соответствующий ему синус.
Например, если известно, что косинус угла равен 0,5, то можно найти в таблице ближайшее значение косинуса. Если в таблице найдено значение косинуса 0,5, то синус угла будет тем же самым значением, но с противоположным знаком. В данном случае синус будет равен -0,5.
Таблицы синусов и косинусов могут быть представлены в различных форматах, например, в таблицах, графиках или даже в приложениях и онлайн-ресурсах. Выбор формата зависит от ваших предпочтений и доступности материалов.
Использование таблиц синусов и косинусов может значительно упростить вычисления и сделать процесс нахождения синуса угла по известному значению косинуса более эффективным и быстрым.
Использование калькуляторов или математических программ

Использование калькуляторов или математических программ весьма удобно и эффективно при решении сложных математических задач. Они позволяют с легкостью находить синус угла, зная косинус, а также выполнять другие сложные вычисления.
Калькуляторы и математические программы обладают широким набором функций, включая функции тригонометрии. Они могут рассчитывать синусы, косинусы и другие тригонометрические функции с высокой точностью и быстротой. Все, что нужно сделать, это ввести значение косинуса угла и нажать на кнопку, чтобы получить значение синуса.
Такие программы для вычисления синуса по косинусу могут быть полезны в разных областях, включая научные исследования, инженерные расчеты и учебу. Они позволяют сократить время, затрачиваемое на решение задач, и уменьшить вероятность ошибок.
Однако, необходимо помнить, что при использовании калькуляторов и математических программ необходимо учитывать особенности округления и погрешности, которые могут возникать в результате арифметических операций. Поэтому всегда стоит проверять полученные значения с помощью других методов или относительно известных фактов.






