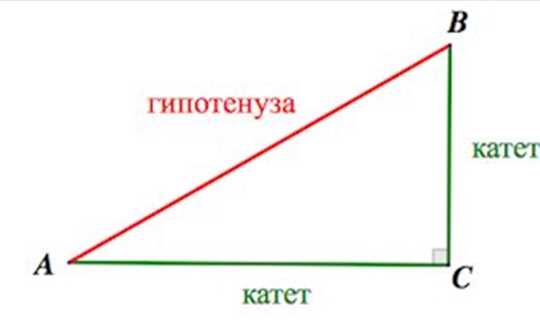
Прямоугольный треугольник АВС – это треугольник, у которого один из углов равен 90 градусам. Одним из основных элементов такого треугольника является синус угла A.
Для нахождения синуса угла A в прямоугольном треугольнике АВС, нужно разделить длину противолежащей стороны катетом АВ на гипотенузу, обозначенную символом С. То есть sin A = AB/AC.
Чтобы проиллюстрировать это, рассмотрим пример. Допустим, угол A равен 30 градусам, сторона АВ равна 5 см, а гипотенуза АС равна 10 см. Тогда, для нахождения синуса A подставим значения в формулу: sin 30° = 5/10 = 0.5.
Таким образом, синус угла A в прямоугольном треугольнике АВС можно легко найти, используя соотношение между длинами сторон катета и гипотенузы.
Описание прямоугольного треугольника АВС
В прямоугольном треугольнике угол, равный 90 градусов, называется прямым углом и обозначается символом «∠«. Он расположен напротив самой длинной стороны треугольника, которая называется гипотенузой и обозначается символом «с«. Оставшиеся две стороны называются катетами: один катет называется «а«, а другой — «б«.
Прямоугольные треугольники широко применяются в геометрии, физике, инженерии и других науках. Они позволяют решать различные задачи, такие как определение длин сторон треугольника, нахождение значений углов, расчет площади и т.д. Применение прямоугольных треугольников также можно найти в реальной жизни, например, при проектировании зданий, строительстве, навигации и многих других областях.
В прямоугольном треугольнике синус угла может быть найден с помощью отношения длины противолежащего катета к гипотенузе:
sin A = a / c
Где «sin A» — синус угла «A«, «a» — длина противолежащего катета и «c» — длина гипотенузы.
Пример расчета:

Допустим, у нас есть прямоугольный треугольник АВС, в котором длина гипотенузы составляет 10 см, а длина одного из катетов равна 6 см. Нам нужно найти значение синуса угла А.
Используя формулу sin A = a / c, подставим известные значения: sin A = 6 / 10 = 0,6.
Таким образом, синус угла А равен 0,6.
Использование прямоугольных треугольников и расчетов, таких как нахождение синуса угла, помогает решать разнообразные задачи и получать точные результаты. Умение работать с прямоугольными треугольниками и их свойствами является важным навыком во многих областях знаний.
Формула для нахождения синуса угла А в прямоугольном треугольнике
Для расчета значения синуса угла А в прямоугольном треугольнике АВС используется следующая формула:
sin A = противоположный катет / гипотенуза
То есть, чтобы найти синус угла А, нужно разделить длину противоположенного катета на длину гипотенузы.
Применяя эту формулу, можно получить информацию о величине синуса угла А в конкретном прямоугольном треугольнике. Рассмотрим пример для наглядности.
Предположим, что в треугольнике АВС угол А равен 30 градусов, а длина гипотенузы составляет 10 см. Наша задача — найти длину противоположенного катета и значение синуса угла А.
Для начала, воспользуемся тригонометрической функцией синуса:
sin 30° = противоположный катет / гипотенуза
Известно, что sin 30° = 0.5 (вы можете узнать это значение синуса по таблице или с помощью калькулятора). Подставляем в формулу:
0.5 = противоположный катет / 10
Чтобы найти длину противоположенного катета, перемножаем обе стороны на 10:
0.5 * 10 = противоположный катет
Противоположный катет равен 5 см.
Таким образом, мы нашли длину противоположенного катета и значение синуса угла А для данного прямоугольного треугольника.
Используя формулу sin A = противоположный катет / гипотенуза, вы можете найти синус угла А в любом другом прямоугольном треугольнике. Важно помнить, что значения катетов и гипотенузы должны быть измерены или известны для корректных расчетов.
Примеры расчетов sin A
В данной статье мы рассмотрели подробное объяснение и примеры расчета sin A в прямоугольном треугольнике. Зная значения сторон треугольника, мы можем использовать тригонометрическую функцию sin для определения угла A.
Для примера, допустим, что у нас есть прямоугольный треугольник ABC, где сторона AB — противолежащая сторона угла A, сторона BC — прилежащая сторона угла A, а сторона AC — гипотенуза. Допустим, что гипотенуза AC равна 5 см, а сторона BC равна 3 см.
Используя теорему Пифагора, мы можем найти сторону AB. Значение стороны AB будет равно 4 см. Далее, мы можем использовать соотношение sin A = AB / AC для расчета sin A. В нашем случае, sin A = 4 / 5 = 0.8.






