- Определение параллелограмма
- Основные характеристики
- Стороны и углы
- Диагонали
- Высота и площадь
- Определение произвольной точки Е
- Формула для вычисления площади параллелограмма
- Определение координат точек А, В, С и D
- Способы определения координат
- Пример задачи
- Приведение примера координатных значений для эксперимента
- Заключение

Никогда не задумывались о том, как найти решение выбор произвольной точки Е внутри параллелограмма ABCD? Это может показаться сложной задачей, но на самом деле существует простой и эффективный способ решения. Все, что вам нужно сделать — это использовать свойства параллелограмма и основные принципы геометрии. Сначала найдите середины сторон параллелограмма, соедините их и получите диагонали. Затем проведите прямую через точку Е параллельно одной из диагоналей. В точке пересечения этой прямой с другой диагональю вы найдете искомую точку F. Итак, теперь вы знаете, как найти решение выбор произвольной точки Е внутри параллелограмма ABCD. Не стесняйтесь использовать этот метод и наслаждайтесь решением геометрических задач!
Определение параллелограмма
Чтобы лучше представить себе, что такое параллелограмм, давайте представим, что у нас есть две параллельные линии, а между ними проведены отрезки, соединяющие их. Если мы теперь соединим эти отрезки концами, мы получим параллелограмм. Это похоже на простой повседневный пример — дверь нашего дома. Если взглянуть на нее сверху, то скорее всего увидим параллелограмм: две стороны (боковые) и две противоположные (верхняя и нижняя).
Параллелограмм имеет несколько ключевых свойств:
- Противоположные стороны параллельны и равны.
- Противоположные углы параллельны и равны.
- Диагонали параллелограмма делятся пополам.
- Сумма углов параллелограмма равна 360 градусов.
С учетом этих свойств, мы можем легко распознать и определить параллелограмм в различных ситуациях. Например, если у нас есть четыре стороны, которые равны и параллельны попарно, то это уже является признаком параллелограмма. Также, если у нас есть две пары равных противоположных углов, это также говорит нам о параллелограмме.
Параллелограммы широко применяются в различных областях, таких как геометрия, физика, инженерия и дизайн. Их свойства и формы делают их полезными для построения и проектирования различных структур и объектов. Они также помогают нам понять и изучать различные математические и физические концепции.
Таким образом, параллелограмм — это важная геометрическая фигура, которая имеет множество интересных свойств и применений. Понимание и определение параллелограмма помогает нам лучше анализировать и применять его в различных ситуациях. Теперь, когда вы знаете, что такое параллелограмм, вы можете легко распознать его в окружающем мире и использовать его в своих проектах и исследованиях.
Основные характеристики
Стороны и углы

В параллелограмме ABCD каждая сторона имеет противоположную параллельную сторону равной длины. Это значит, что AB = CD и BC = AD. Кроме того, каждый угол параллелограмма равен своему противолежащему углу. То есть угол A равен углу C, а угол B равен углу D.
Диагонали
В параллелограмме ABCD существуют две диагонали — AC и BD. Диагонали делятся пополам и пересекаются в точке O, которая является их серединой. То есть AO = OC и BO = OD.
Высота и площадь
Высота параллелограмма — это перпендикуляр, опущенный из одного угла на противоположную сторону. Она соединяет все углы параллелограмма со сторонами, образуя четыре прямоугольных треугольника. Произведение длины стороны параллелограмма на его высоту равно его площади.
Определение произвольной точки Е
Когда мы ищем решение выбора произвольной точки Е внутри параллелограмма ABCD, мы можем использовать свойство параллелограмма, что диагонали пересекаются в середине. Таким образом, мы можем выбрать точку Е так, чтобы она располагалась на одной из диагоналей и делила ее пополам. Например, мы можем выбрать точку Е так, чтобы AE равнялась EC или BE равнялась ED.
Вот основные характеристики параллелограмма и подходы к выбору произвольной точки E внутри него. Вы можете использовать эти знания, чтобы легко решить задачу, связанную с параллелограммом и его точкой Е. Удачи в вашем исследовании параллелограммов!
Формула для вычисления площади параллелограмма
Если мы знаем длину одной из сторон параллелограмма и высоту, опущенную на эту сторону, то мы можем легко вычислить его площадь. Формула для вычисления площади параллелограмма:
S = a * h
Где:
- S — площадь параллелограмма
- a — длина одной стороны параллелограмма
- h — высота, опущенная на эту сторону параллелограмма
Для нахождения площади параллелограмма ABCD достаточно знать длину одной из его сторон и длину высоты, опущенной на эту сторону.
Вычисление площади параллелограмма является простым и эффективным способом определения площади этой фигуры. Уверен, что с помощью данной формулы вы с легкостью сможете найти площадь параллелограмма ABCD или любого другого параллелограмма.
Определение координат точек А, В, С и D
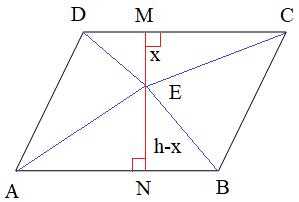
Для решения задачи по выбору произвольной точки Е внутри параллелограмма ABCD нам необходимо сначала определить координаты вершин данного параллелограмма.
Параллелограмм — это четырехугольник, у которого стороны попарно параллельны. Особенностью параллелограмма является равенство противоположных сторон и противоположных углов.
Итак, пусть у нас есть параллелограмм ABCD.
Для определения координат точек A, B, C и D мы можем использовать различные методы. Рассмотрим один из них:
1. Если нам даны координаты вершин параллелограмма A(x1, y1), B(x2, y2), C(x3, y3), то мы можем легко найти координаты точки D.
Сначала найдем вектор АВ, который определяется следующим образом:
AB = (x2 — x1, y2 — y1)
Затем найдем координаты точки D, используя координаты вершины C и вектор АВ:
D(x4, y4) = C(x3, y3) + AB = (x3 + (x2 — x1), y3 + (y2 — y1))
2. Другой способ для определения координат всего параллелограмма состоит в использовании векторов.
Рассмотрим параллелограмм ABCD со сторонами AB, BC, CD и DA.
AB = BA = (x2 — x1, y2 — y1)
BC = CB = (x3 — x2, y3 — y2)
CD = DC = (x4 — x3, y4 — y3)
DA = AD = (x1 — x4, y1 — y4)
Итак, мы определили координаты точек A, B, C и D, используя либо формулу для нахождения координат точки D, либо используя векторы AB, BC, CD и DA. Это поможет нам в дальнейшем в выборе произвольной точки Е внутри параллелограмма ABCD и решении поставленной задачи.
Способы определения координат
- Графический метод: самый простой и интуитивный способ определения координат точки на плоскости. Мы можем использовать сетку и линейку, чтобы измерять расстояния по осям и находить координаты точки.
- Алгебраический метод: этот метод используется в ряде задач аналитической геометрии, где нужно выразить координаты точки через известные данные. Например, если у нас есть уравнение прямой или окружности, мы можем подставить значения координат точки в это уравнение и решить его для неизвестных.
- Использование формул: существует несколько формул, которые позволяют определить координаты точек в различных геометрических фигурах. Например, в треугольнике можно использовать формулу скалярного произведения для определения координат точки пересечения медиан. В параллелограмме можно использовать формулу для определения координат центра масс.
Пример задачи
Давайте рассмотрим пример задачи, связанной с нахождением координат точки внутри параллелограмма ABCD. Пусть у нас есть параллелограмм с вершинами A(1, 1), B(4, 2), C(3, 5) и D(0, 4). Нам нужно найти координаты произвольной точки Е внутри этого параллелограмма.
Чтобы решить эту задачу, мы можем использовать графический метод, алгебраический метод или формулы для параллелограмма, в зависимости от доступных данных.
- Если у нас есть возможность построить график параллелограмма и точки E на нем, мы можем использовать графический метод для определения координат. Ниже представлен график параллелограмма ABCD и точки E.

Из графика мы можем прочитать координаты точки E, которые могут быть приближенно равны (2, 3).
- Если у нас есть уравнения прямых AB и CD, мы можем использовать алгебраический метод для определения координат точки E. Подставив уравнения прямых в систему уравнений и решив ее, мы можем найти значения для неизвестных переменных и, соответственно, координаты точки E.
Конечно, в каждой задаче мы должны принимать во внимание доступные данные и контекст задачи. Возможно, при данном условии задачи мы должны использовать формулы для нахождения координат точек в параллелограмме.
Независимо от используемого метода, определение координат точек является важным навыком в аналитической геометрии и может использоваться в различных контекстах и задачах. Освоение различных методов и формул позволит нам эффективно работать с координатами и решать геометрические задачи.
Приведение примера координатных значений для эксперимента
Представим, что координаты вершин параллелограмма ABCD заданы следующим образом:
| Вершина | x | y |
|---|---|---|
| A | 0 | 0 |
| B | 4 | 0 |
| C | 6 | 4 |
| D | 2 | 4 |
С помощью этих координат мы можем определить различные варианты для точки Е и увидеть, как они располагаются внутри параллелограмма. Возьмем, например, следующие координаты:
- x = 2, y = 2
- x = 3, y = 1
- x = 5, y = 3
Используя эти значения, мы можем построить точки Е на координатной плоскости и убедиться, что они действительно находятся внутри параллелограмма ABCD. Также можно выполнять вычисления для каждого варианта, чтобы увидеть, как изменяются соответствующие значения и свойства.
Все эти эксперименты позволяют нам более глубоко понять структуру параллелограмма и его свойства. Они помогают нам найти решение для выбора произвольной точки Е и позволяют пролить свет на процесс решения геометрических задач. Поэтому, проведя подобные эксперименты с различными значениями координат, мы сможем получить более широкое представление об исследуемой теме и возможных решениях.
Заключение
Геометрический подход основан на использовании свойств параллелограмма и позволяет найти координаты точки Е с помощью построений и вычислений с соответствующими векторами. Этот подход требует хороших геометрических навыков и может быть сложным при работе с параллелограммами нестандартной формы.
Аналитический подход основан на использовании алгебраических методов и позволяет найти координаты точки Е с помощью системы уравнений. Этот подход более универсальный и позволяет решать задачу для любых параллелограммов, но требует знания алгебры и решения систем уравнений.
Итак, выбор произвольной точки Е внутри параллелограмма ABCD может быть решен различными способами, в зависимости от наших навыков и предпочтений. Геометрический подход требует геометрических навыков, а аналитический подход – алгебраических. Используйте тот подход, который наиболее удобен и понятен для Вас.






