Как найти расстояние от точки M до прямой: подробное руководство и примеры Сайт.com

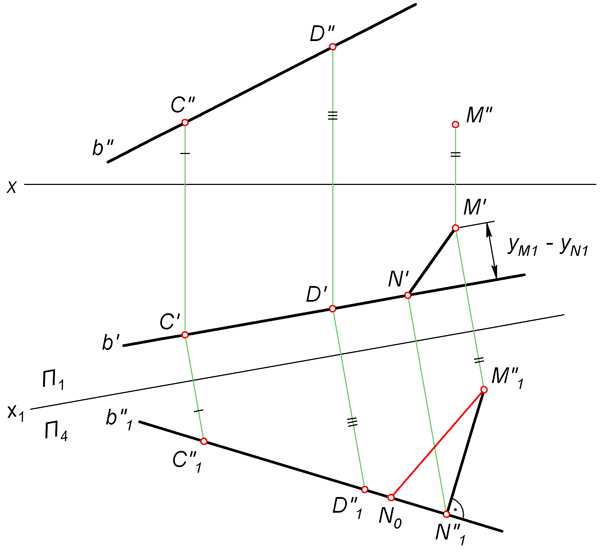
Если вам когда-либо приходилось вычислять расстояние от точки до прямой, то вы знаете, что это задача, требующая некоторых математических навыков. Однако, с правильным подходом и пониманием основных концепций, это становится достаточно простой задачей.

В этом подробном руководстве мы рассмотрим, как найти расстояние от точки M до прямой, используя геометрические и алгебраические методы. Мы также рассмотрим несколько примеров, чтобы помочь вам лучше понять процесс решения таких задач.

Не волнуйтесь, если математика не ваша сильная сторона – наш подробный материал и примеры помогут разобраться в этой теме и успешно решать подобные задачи.

Как найти расстояние от точки M до прямой: подробное руководство и примеры

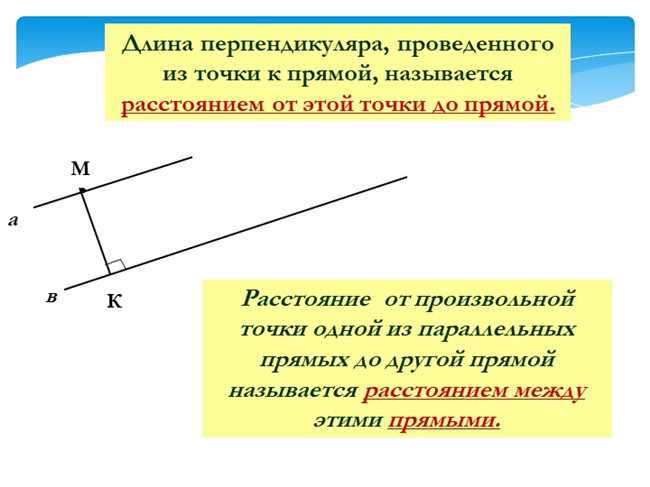
Вы когда-нибудь задумывались, как найти расстояние от точки до прямой? Возможно, вам приходилось решать подобные задачи в школе или университете, или вам просто интересно узнать, как это делается. Независимо от причины, в этом руководстве я расскажу вам о методах и примерах расчета расстояния от точки M до прямой.

Прежде всего, давайте определимся с терминологией. В нашем случае, точка M — это точка на плоскости, а прямая — это прямая линия, которая может представлять собой график математической функции или просто линию, заданную двумя точками.

Теперь перейдем к методам расчета расстояния от точки M до прямой. Существует несколько способов, но я расскажу вам о двух наиболее распространенных:

1. Формула расстояния от точки до прямой

Первым методом является использование формулы расстояния от точки до прямой. Эта формула основана на принципе минимального расстояния между точкой и прямой, которое определяется перпендикулярной линией, соединяющей точку и линию.

Формула имеет следующий вид:

d = |Ax + By + C| / sqrt(A^2 + B^2)

Где A, B и C — это коэффициенты уравнения прямой вида Ax + By + C = 0, а x и y — координаты точки M.

Давайте рассмотрим пример использования этой формулы. Предположим, что у нас есть точка M с координатами (2, 3) и уравнение прямой 2x + 3y — 6 = 0. Как найти расстояние от точки M до этой прямой?

Сначала мы должны найти коэффициенты A, B и C. В данном случае A = 2, B = 3 и C = -6. Затем мы можем подставить значения в формулу:

d = |2 * 2 + 3 * 3 — 6| / sqrt(2^2 + 3^2)

d = |13 — 6| / sqrt(4 + 9)

d = 7 / sqrt(13)

Полученный результат, округленный до сотых, составляет примерно 1.58. Таким образом, расстояние от точки M до прямой 2x + 3y — 6 = 0 равно примерно 1.58.

2. Перпендикулярная линия и точка прямой

Второй метод основан на нахождении перпендикулярной линии от точки до прямой и нахождении точки на прямой, ближайшей к заданной точке. Расстояние от этой точки до исходной точки будет являться искомым расстоянием.

Приведу пример для наглядности. Предположим, что у нас есть точка M с координатами (4, 7) и прямая, проходящая через точку A(2, 3) и B(6, 9). Как найти расстояние от точки M до этой прямой?

Сначала мы рассчитываем угловой коэффициент прямой через точки A и B:

м = (y2 — y1) / (x2 — x1)

м = (9 — 3) / (6 — 2)

м = 6 / 4

м = 1.5

Затем мы используем найденный угловой коэффициент для нахождения уравнения прямой, проходящей через точку M и перпендикулярной главной прямой:

y — y1 = м(x — x1)

y — 7 = 1.5(x — 4)

Решив это уравнение, мы находим точку пересечения прямой и перпендикулярной линии. В данном случае, x = 4, y = 7. Эта точка находится на исходной прямой и ближе всего к заданной точке M. Расстояние от точки M до этой точки будет являться искомым расстоянием.

Важно помнить, что в некоторых случаях перпендикулярная линия может находиться за пределами отрезка, образованного точками A и B. В этом случае, нужно проверить, лежит ли найденная точка пересечения между A и B и, в противном случае, использовать одну из граничных точек для расчета расстояния.

Вот и все! Теперь вы знаете, как найти расстояние от точки M до прямой. Уверены, что вы можете применить эти методы к любым задачам и получить правильные ответы. Если у вас есть какие-либо вопросы, не стесняйтесь их задавать. Желаю вам успехов в изучении математики и ее применении в реальной жизни!

Раздел 1: Определение понятий

Прежде чем мы погрузимся в детали и узнаем, как найти расстояние от точки M до прямой, давайте определим важные понятия, которые будут использоваться в дальнейшем.

Точка — это основной элемент в геометрии, который не имеет размера и представляет собой только положение в пространстве.

Прямая — это множество точек, которые расположены на одной линии, и не имеют ни начала, ни конца.

Расстояние — это мера протяженности между двумя объектами. В контексте нашей темы, расстояние будет выражать удаление от точки M до прямой.

Теперь, когда мы знаем основные определения, давайте перейдем к более подробному изучению того, как точно найти расстояние от точки M до прямой.

Раздел 2: Методы определения расстояния от точки до прямой

Когда мы говорим о нахождении расстояния от точки до прямой, существует несколько методов, которые могут помочь нам в этом. Давайте рассмотрим каждый из них подробнее.

Метод 1: Формула расстояния

Первый метод, который мы рассмотрим, основывается на использовании формулы расстояния между точкой и прямой. Для того чтобы применить этот метод, нам необходимо знать координаты точки и уравнение прямой. Формула для нахождения расстояния от точки до прямой выглядит следующим образом:

d = |Ax + By + C| / sqrt(A^2 + B^2)

Где A, B и C — коэффициенты уравнения прямой, а x и y — координаты точки.

Давайте рассмотрим пример, чтобы увидеть, как это работает:

Уравнение прямой: 2x + 3y — 6 = 0

Координаты точки: M(4, 2)

Подставляя значения в формулу расстояния, мы получим:

d = |2 * 4 + 3 * 2 — 6| / sqrt(2^2 + 3^2)

d = |8 + 6 — 6| / sqrt(4 + 9)

d = |8| / sqrt(13)

d ≈ 8 / 3.61

d ≈ 2.21

Таким образом, расстояние от точки M(4, 2) до прямой 2x + 3y — 6 = 0 составляет примерно 2.21 единицы.

Метод 2: Свойство перпендикулярности

Второй метод, которым мы можем воспользоваться, основывается на свойстве перпендикулярности. Если мы проведем перпендикуляр от данной точки до прямой, то расстояние от точки до прямой будет равно длине этого перпендикуляра.

Давайте рассмотрим пример, чтобы прояснить этот метод:

Уравнение прямой: 2x + 3y — 6 = 0

Координаты точки: M(4, 2)

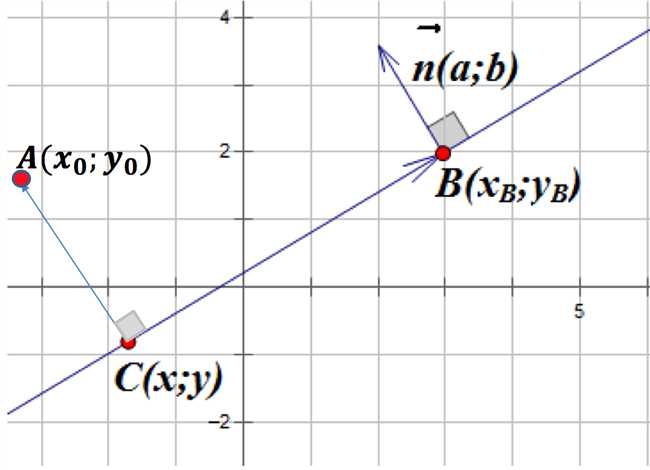
Прямая 2x + 3y — 6 = 0 имеет нормальный вектор (2, 3). Проведем перпендикуляр от точки M(4, 2) к данной прямой. Нормальный вектор данного перпендикуляра будет (-3, 2). Найдем уравнение прямой, проходящей через точку M(4, 2) и параллельной перпендикуляру.

Уравнение прямой: -3x + 2y — 2 = 0

Теперь нам остается найти точку пересечения прямых 2x + 3y — 6 = 0 и -3x + 2y — 2 = 0. Решая систему этих уравнений, мы найдем точку пересечения (2.4, 1.2).

Зная координаты точки пересечения (2.4, 1.2) и точки M(4, 2), мы можем вычислить расстояние между ними, используя формулу расстояния:

d = sqrt((4 — 2.4)^2 + (2 — 1.2)^2)

d ≈ sqrt(1.6^2 + 0.8^2)

d ≈ sqrt(2.56 + 0.64)

d ≈ sqrt(3.2)

d ≈ 1.79

Таким образом, расстояние от точки M(4, 2) до прямой 2x + 3y — 6 = 0 составляет примерно 1.79 единицы.

Метод 3: Геометрический метод

Третий метод, который мы рассмотрим, основан на использовании геометрического подхода. Для определения расстояния от точки до прямой, можно построить прямую, перпендикулярную данной прямой, и найти точку пересечения этой прямой с перпендикуляром, проведенным через данную точку.

Давайте рассмотрим пример, чтобы увидеть, как это работает:

Уравнение прямой: 2x + 3y — 6 = 0

Координаты точки: M(4, 2)

Для построения перпендикуляра проведем прямую через точку M(4, 2), параллельную данной прямой. Зная, что нормальный вектор данной прямой равен (2, 3), нормальный вектор перпендикуляра будет (-3, 2). Используя координаты точки M(4, 2) и нормальный вектор перпендикуляра (-3, 2), мы можем найти уравнение перпендикуляра.

Уравнение перпендикуляра: -3x + 2y — 2 = 0

Теперь нам остается найти точку пересечения прямых 2x + 3y — 6 = 0 и -3x + 2y — 2 = 0. Решая систему этих уравнений, мы найдем точку пересечения (2.4, 1.2).

Зная координаты точки пересечения (2.4, 1.2) и точки M(4, 2), мы можем вычислить расстояние между ними, используя формулу расстояния:

d = sqrt((4 — 2.4)^2 + (2 — 1.2)^2)

d ≈ sqrt(1.6^2 + 0.8^2)

d ≈ sqrt(2.56 + 0.64)

d ≈ sqrt(3.2)

d ≈ 1.79

Таким образом, расстояние от точки M(4, 2) до прямой 2x + 3y — 6 = 0 составляет примерно 1.79 единицы.

Есть несколько методов определения расстояния от точки до прямой, и выбор метода зависит от ситуации и доступных данных. Важно понимать, что каждый метод имеет свои ограничения и требования, поэтому важно выбирать наиболее подходящий метод для конкретной ситуации.

Раздел 3: Примеры решения задач

Теперь, когда мы разобрались с основными понятиями и формулами, пришло время рассмотреть несколько примеров решения задач по нахождению расстояния от точки M до прямой. Эти примеры помогут нам лучше понять, как применять теорию на практике.

Пример 1:

Пусть у нас есть прямая, заданная уравнением 3x + 4y — 7 = 0, и точка M(2, 5). Найдем расстояние от точки M до этой прямой.

Шаг 1: Запишем уравнение прямой соответствующим образом: 3x + 4y — 7 = 0.

Шаг 2: Найдем коэффициенты A, B и C в уравнении прямой. В данном случае, A = 3, B = 4, C = -7.

Шаг 3: Используем формулу для расстояния от точки до прямой:

d = |Ax + By + C| / sqrt(A^2 + B^2)

Подставим значения для A, B, C и координат точки M в формулу:

Таким образом, расстояние от точки M(2, 5) до прямой 3x + 4y — 7 = 0 равно 3.8.

Пример 2:

Пусть теперь у нас есть прямая, заданная параметрическим уравнением:

x = t + 1

y = 3t — 2

И точка M(2, 5). Найдем расстояние от точки M до этой прямой.

Шаг 1: Запишем уравнение прямой в общем виде: y = 3x — 5.

Шаг 2: Найдем коэффициенты A, B и C в уравнении прямой. В данном случае, A = 3, B = -1, C = -5.

Шаг 3: Используем формулу для расстояния от точки до прямой:

d = |Ax + By + C| / sqrt(A^2 + B^2)

Подставим значения для A, B, C и координат точки M в формулу:

Таким образом, расстояние от точки M(2, 5) до прямой y = 3x — 5 примерно равно 1.26.

Примеры, представленные выше, позволяют нам увидеть, как применять теорию для нахождения расстояния от точки до прямой. При решении задач обратите внимание на формулу для расстояния и овладейте навыками подстановки значений и вычислений. Перед тем как перейти к следующему разделу, попробуйте решить несколько задач самостоятельно, чтобы закрепить материал. Удачи!

Раздел 4: Важные советы и рекомендации

В этом разделе мы хотим поделиться с вами некоторыми важными советами и рекомендациями, которые помогут вам найти расстояние от точки M до прямой более эффективно. При следовании этим советам вы сможете достичь точности и точности в своих вычислениях.

1. Правильно выбирайте систему координат

Перед тем как начать решать задачу, убедитесь, что вы правильно выбрали систему координат. Это поможет вам визуализировать прямую и точку M, а также упростить последующие математические вычисления.

2. Используйте соответствующие формулы

В нашей статье вы найдете подробное объяснение формулы для вычисления расстояния от точки M до прямой. Убедитесь, что вы правильно применяете эти формулы и учтите все необходимые параметры, такие как координаты точек и уравнение прямой.

3. Анализируйте результаты

После вычисления расстояния от точки M до прямой, внимательно изучите полученные результаты. Проанализируйте, в какой форме они представлены — абсолютное значение, корень из суммы квадратов или в виде уравнения. Это поможет вам понять, насколько близко или далеко находится точка М от прямой.

Следуя этим важным советам и рекомендациям, вы сможете справиться с задачей нахождения расстояния от точки M до прямой более эффективно и точно. Постепенно, с практикой, вы сможете развить свои навыки в этой области и успешно применять их в решении подобных задач.