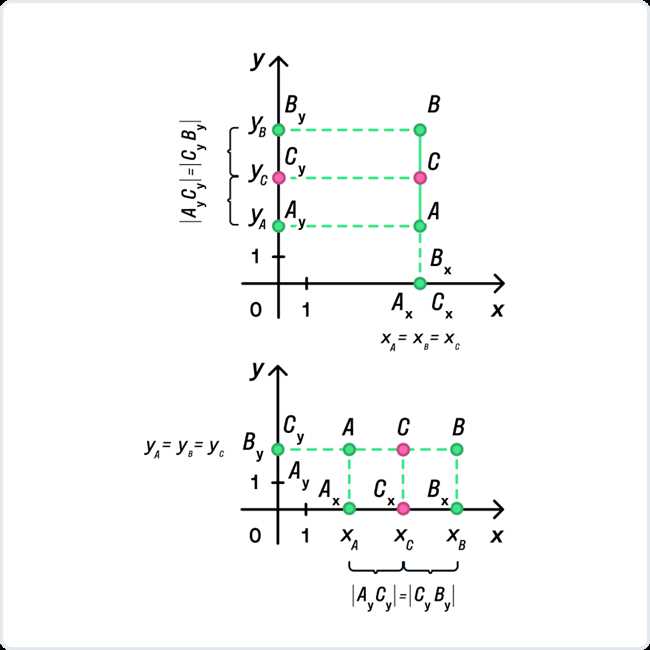
Когда мы хотим найти расстояние от точки A до середины отрезка ВС в системе координат, нам приходится использовать определенные математические формулы и методы. Это позволяет нам точно определить расстояние и получить результаты, которые можно использовать в дальнейших вычислениях или решении задач. Одним из основных методов является использование координатных формул, которые позволяют найти координаты середины отрезка ВС. Затем мы можем использовать формулу расстояния между двумя точками в системе координат, чтобы определить расстояние от точки A до этой середины. Важно правильно применять данные формулы и использовать соответствующие значения координат, чтобы получить точный результат.
Определение системы координат
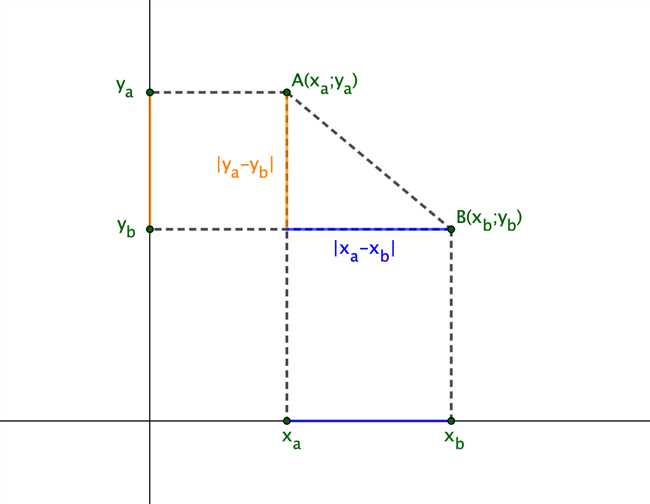
Точка в системе координат определяется своими координатами, которые представляют собой числа. Горизонтальная ось называется осью абсцисс, а вертикальная ось — осью ординат. Координаты точки в системе координат записываются в виде упорядоченной пары чисел (x, y), где x — это значение на оси абсцисс, а y — на оси ординат.
Если требуется найти расстояние от точки A до середины отрезка ВС в системе координат, можно воспользоваться формулой расстояния между двумя точками.
Для начала необходимо найти координаты точек В и С. Затем находим координаты точки М, которая является серединой отрезка ВС. Для этого мы можем использовать формулу середины отрезка: (xМ)=(xВ+xC)/2 и (yМ)=(yВ+yC)/2. Зная координаты точки A и точки М, можно использовать формулу расстояния между двумя точками:
√[(xМ-xA)2 + (yМ-yA)2]
Выполнив несложные вычисления, можно определить расстояние от точки A до середины отрезка ВС в системе координат.
Нахождение середины отрезка ВС
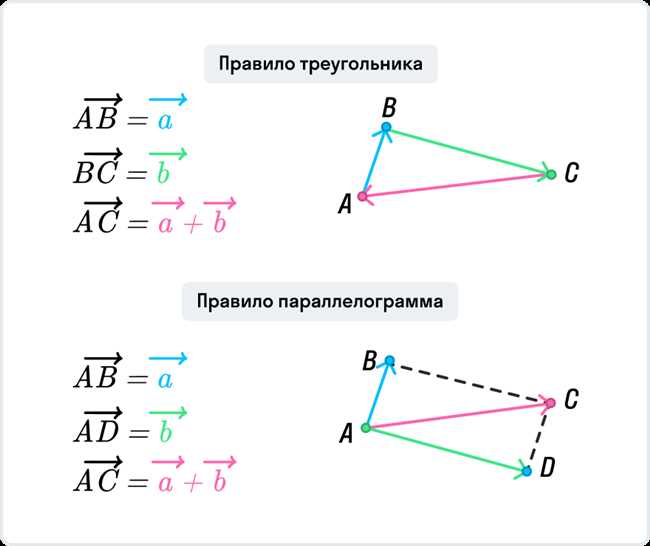
Чтобы найти середину отрезка ВС в системе координат, нужно знать координаты точек В и С.
Для начала, обозначим координаты точки В как (X1, Y1), а координаты точки С как (X2, Y2).
Середина отрезка ВС имеет координаты (Xсредн., Yсредн.) и может быть найдена по следующим формулам:
- Xсредн. = (X1 + X2) / 2
- Yсредн. = (Y1 + Y2) / 2
Используя эти формулы, мы можем легко найти середину отрезка ВС. Подставляя значения координат точек В и С в формулы, получаем координаты середины отрезка.
Например, пусть точка В имеет координаты (2, 4), а точка С имеет координаты (6, 10). С помощью формул нахождения середины отрезка, мы можем найти его координаты:
- Xсредн. = (2 + 6) / 2 = 4
- Yсредн. = (4 + 10) / 2 = 7
Таким образом, середина отрезка ВС в данном случае имеет координаты (4, 7).
Найденные координаты середины отрезка ВС позволяют нам определить его положение в системе координат и использовать эту информацию для решения различных задач. Например, мы можем использовать координаты середины отрезка для нахождения расстояния от точки A до середины отрезка ВС.
В общем случае, расстояние от точки A до середины отрезка ВС можно найти с помощью формулы:
расстояние = √((Xсредн. — Xa)^2 + (Yсредн. — Ya)^2)
Где (Xa, Ya) — координаты точки A.
Используя найденные ранее координаты середины (4, 7) и координаты точки A (3, 5), мы можем вычислить расстояние от точки A до середины отрезка ВС:
расстояние = √((4 — 3)^2 + (7 — 5)^2) = √(1 + 4) = √5
Таким образом, расстояние от точки A до середины отрезка ВС в данном случае равно √5.
В итоге, нахождение середины отрезка ВС и расстояния от точки A до этой середины является важной задачей в системе координат. В геометрии, это позволяет нам определить положение точки относительно отрезка и использовать эту информацию для решения других задач.
Расчет расстояния от точки A до середины отрезка ВС
Для определения расстояния от точки A до середины отрезка ВС в системе координат, можно использовать формулу:
d = sqrt((xC — xA)2 + (yC — yA)2) / 2
где d представляет собой искомое расстояние, xA и yA — координаты точки A, xC и yC — координаты точки C.
Для более наглядного понимания принципа расчета расстояния от точки A до середины отрезка ВС, можно воспользоваться следующим примером:
- Пусть точка A имеет координаты (2, 3).
- Пусть точка B имеет координаты (4, 7), а точка C — (8, 1).
Замечаем, что середина отрезка ВС будет иметь координаты ((4 +  / 2, (7 + 1) / 2) = (6, 4).
/ 2, (7 + 1) / 2) = (6, 4).
Подставим значения в формулу расчета расстояния:
d = sqrt((6 — 2)2 + (4 — 3)2) / 2 = sqrt(16 + 1) / 2 = sqrt(17) / 2 ≈ 2.12 см
Таким образом, расстояние от точки A до середины отрезка ВС составляет примерно 2.12 см.
Использование данной формулы позволяет легко и быстро рассчитывать расстояние от точки A до середины отрезка ВС в системе координат, что является важным инструментом визуализации и решения геометрических задач.






