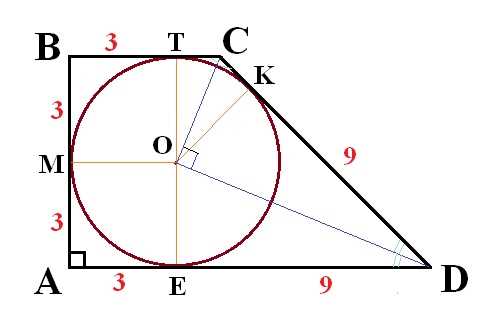
Когда речь идет о прямоугольной трапеции, вписанной около окружности, важно знать, как найти радиусы вписанных окружностей. Воспользуйтесь следующей стратегией. Во-первых, обратите внимание на основания трапеции — это отрезки, которые соединяют две противоположные вершины трапеции. Затем, найдите среднюю линию, которая является отрезком, соединяющим середины оснований трапеции. Для поиска угла, образованного прямым углом и радиусом, воспользуйтесь теоремой Пифагора. Выразив радиус через длину основания и среднюю линию, вы сможете найти радиусы вписанных окружностей в прямоугольную трапецию. Не забывайте использовать формулы для нахождения площадей и длин отрезков.
Определение прямоугольной трапеции
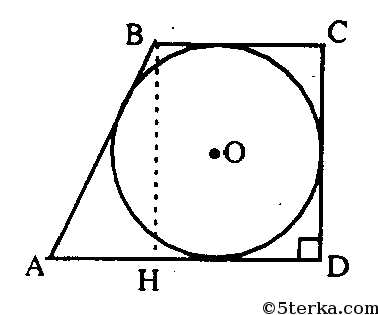
Пример прямоугольной трапеции:
| Верхнее основание | ||||
| Боковая сторона | ||||
| Нижнее основание | ||||
| Верхнее основание | ||||
Прямоугольные трапеции очень часто встречаются в различных областях, таких как геометрия, архитектура, инженерное дело и дизайн. Их уникальная форма и свойства делают их идеальными для строительства и создания разнообразных структур.
Понимание определения прямоугольной трапеции важно, чтобы успешно решать задачи, связанные с этой фигурой, в том числе по нахождению радиусов вписанных окружностей.
Измерение радиусов вписанных окружностей
Одним из подходов для измерения радиуса вписанной окружности является использование формулы, которая основывается на определенных характеристиках трапеции. Определяем радиус вписанной окружности можно, зная длины сторон трапеции.
Для прямоугольной трапеции с основаниями a и b, высотой h и диагонали c радиус r вписанной окружности может быть вычислен с помощью следующей формулы:
$$r = \frac{ab(h-sqrt(h^2 + \frac{(b-a)^2}{4}))}{a + b + 2c}$$
Где $sqrt$ — функция квадратного корня, а $ab$ — произведение обоих оснований трапеции.
Эта формула основывается на теореме Бретшнайдера, которая связывает радиус вписанной окружности с диагоналями и основаниями трапеции. Она предоставляет точную информацию о радиусе вписанной окружности в зависимости от размеров трапеции.
Другим способом измерения радиуса вписанной окружности является использование метода геометрической конструкции. Начните с построения прямых линий, параллельных основаниям трапеции, и отметьте точки пересечения этих линий с биссектрисами углов трапеции.
Затем проведите прямую линию, соединяющую эти точки пересечения, и перпендикулярную основанию. Удлините эту линию, чтобы она пересекала диагонали трапеции. Точка пересечения этой линии с диагоналями является центром вписанной окружности, и радиус может быть измерен как расстояние от этой точки до одной из сторон трапеции.
В завершение, измерение радиусов вписанных окружностей в прямоугольной трапеции имеет большое практическое значение для различных областей, включая строительство, дизайн и геометрические вычисления. Этот процесс может быть выполнен с помощью математических формул или геометрической конструкции, в зависимости от доступных инструментов и требований задачи.
Формулы для вычисления радиусов вписанных окружностей
Перед тем, как мы начнем, давайте вспомним некоторые определения, связанные с прямоугольной трапецией. Прямоугольная трапеция — это четырехугольник, у которого две противоположные стороны параллельны и одна пара противоположных сторон перпендикулярны друг к другу. Важно отметить, что две боковые стороны прямоугольной трапеции не параллельны.
Теперь давайте рассмотрим формулы для вычисления радиусов вписанных окружностей в прямоугольную трапецию:
1. Формула для радиуса вписанной окружности, касающейся оснований трапеции:
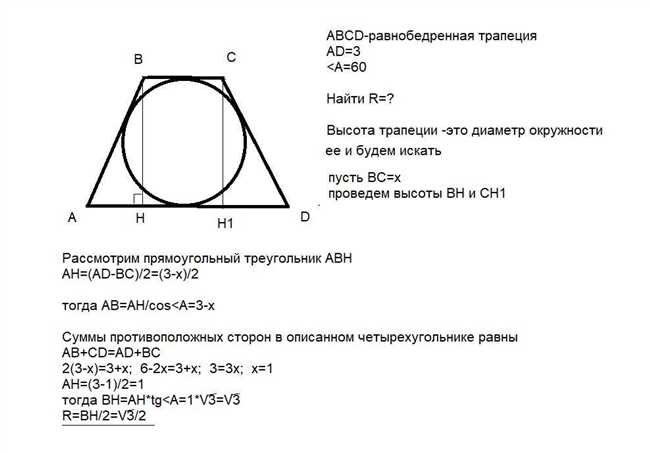
Радиус вписанной окружности, касающейся оснований трапеции, можно найти с помощью следующей формулы:
r1 = (a — b) / 2,
где а и b — длины оснований трапеции.
2. Формула для радиуса вписанной окружности, касающейся боковых сторон трапеции:
Радиус вписанной окружности, касающейся боковых сторон трапеции, можно найти с помощью следующей формулы:
r2 = h / 2,
где h — высота трапеции.
Эти формулы основаны на свойствах прямоугольной трапеции и ее вписанной окружности. Вы можете использовать их для нахождения радиусов вписанных окружностей в прямоугольной трапеции, зная длины оснований и высоту трапеции.
Надеюсь, это поможет вам в изучении данной темы. Если у вас возникли вопросы или вам нужна дополнительная информация, не стесняйтесь задавать их. Желаю вам успехов в изучении математики!
Заключение
В данной статье мы рассмотрели примеры и решение задачи по определению радиусов вписанных окружностей в прямоугольную трапецию. Мы разобрали основные свойства такой трапеции и способы нахождения радиусов окружностей, вписанных в ее основания и диагонали.
В процессе решения задачи нам помогло знание геометрических свойств прямоугольной трапеции, а также умение применять формулы для нахождения радиуса вписанной окружности. Мы выяснили, что радиус окружности, вписанной в основание трапеции, может быть найден с помощью известной длины основания и высоты трапеции.
Также мы узнали, что радиус окружности, вписанной в диагональ трапеции, может быть найден с помощью известных длин боковых сторон трапеции и диагонали.
В итоге, зная эти формулы и совершив несложные вычисления, мы можем определить радиусы вписанных окружностей в прямоугольную трапецию и использовать это знание для решения разнообразных задач из геометрии.






