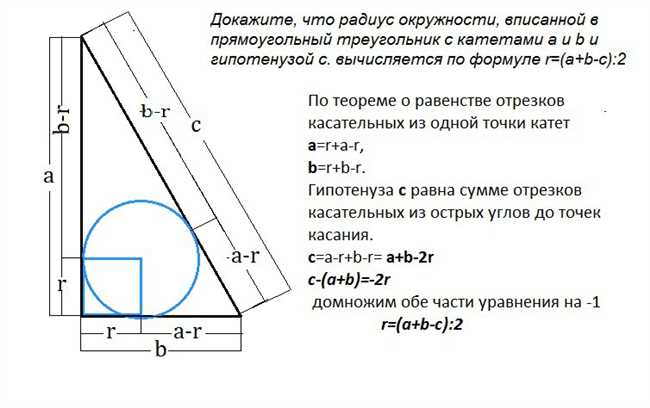
Когда мы сталкиваемся с прямоугольным треугольником, одной из его основных характеристик является вписанная окружность. Чтобы найти радиус этой окружности, нужно знать значения катетов треугольника. Например, предположим, что у нас есть прямоугольный треугольник с катетами 5 и 12. Для расчета радиуса вписанной окружности мы можем использовать формулу, основанную на отношении радиуса, площади треугольника и его периметра. Следуя этой формуле и используя значения катетов, мы сможем найти радиус вписанной окружности и легко визуализировать его в пространстве треугольника.
Определение прямоугольного треугольника

Прямоугольные треугольники имеют множество интересных свойств, которые делают их очень полезными и широко применяемыми в математике и геометрии.
Одно из таких свойств — теорема Пифагора, которая гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Это значит, что если в прямоугольном треугольнике заданы длины двух сторон, то можно легко найти длину третьей стороны.
Прямоугольные треугольники также являются основой для решения множества задач, связанных с расчетами и измерениями. Они применяются в архитектуре, инженерии, физике и других областях науки.
Поэтому знание основных свойств и характеристик прямоугольных треугольников является важной составляющей математической грамотности и может пригодиться в различных сферах жизни.
Описание метода нахождения радиуса вписанной окружности в прямоугольный треугольник
Нахождение радиуса вписанной окружности в прямоугольный треугольник можно выполнить с помощью различных способов и формул, однако один из наиболее эффективных и простых методов основан на использовании свойств треугольника и окружности, вписанной в него.
Итак, имеем прямоугольный треугольник, в котором известны длины катетов. Для начала найдем площадь этого треугольника. По уравнению площади прямоугольного треугольника, оно равно половине произведения длин его катетов: S = (a * b) / 2, где a и b — длины катетов.
Далее, мы знаем, что радиус вписанной окружности в прямоугольный треугольник равен половине суммы катетов, поделенной на гипотенузу. В нашем случае, это будет выглядеть следующим образом: r = (a + b — c) / 2, где r — радиус, a и b — длины катетов, c — длина гипотенузы.
Для нахождения длины гипотенузы с помощью теоремы Пифагора можно воспользоваться формулой c = sqrt(a^2 + b^2), где sqrt — корень квадратный, a и b — длины катетов.
Итак, имея все необходимые значения, подставляем их в формулы и находим радиус вписанной окружности в прямоугольный треугольник.
Мы получим следующую формулу: r = (a + b — sqrt(a^2 + b^2)) / 2.
Возвращаясь к нашему конкретному примеру, где катеты равны 5 и 12, подставляем их в формулу и находим радиус: r = (5 + 12 — sqrt(5^2 + 12^2)) / 2 = (17 — sqrt(169)) / 2 = (17 — 13) / 2 = 4 / 2 = 2.
Итак, радиус вписанной окружности в прямоугольный треугольник с катетами 5 и 12 равен 2 единицам.
Пример вычисления радиуса вписанной окружности в прямоугольный треугольник
В данной статье мы рассмотрели пример вычисления радиуса вписанной окружности в прямоугольный треугольник с катетами 5 и 12.
Для начала, мы использовали формулу для вычисления радиуса вписанной окружности в прямоугольном треугольнике, которая гласит:
r = a + b — c / 2
Где a и b — катеты треугольника, а c — гипотенуза треугольника.
Для нашего примера, a = 5 и b = 12. Теперь нам нужно вычислить гипотенузу треугольника. Для этого мы используем теорему Пифагора:
c^2 = a^2 + b^2
Подставляя значения, получаем:
c^2 = 5^2 + 12^2 = 25 + 144 = 169
Таким образом, гипотенуза треугольника равна 13 (так как квадратный корень из 169 равен 13).
Теперь, мы можем подставить полученные значения в формулу для вычисления радиуса вписанной окружности:
r = 5 + 12 — 13 / 2 = 4
Итак, радиус вписанной окружности в прямоугольный треугольник с катетами 5 и 12 равен 4.






