
Когда речь идет о вписанной окружности в квадрат, многим людям может показаться сложным найти радиус этой окружности. Однако, существуют простые шаги и эффективные методы, которые помогут вам разобраться в этой задаче. Один из способов — использовать теорему Пифагора для определения радиуса вписанной окружности. Этот метод позволяет найти радиус, зная длину стороны квадрата. Еще один подход — использовать свойство вписанной окружности, согласно которому радиус является половиной диагонали квадрата. Таким образом, существуют различные методы для нахождения радиуса вписанной окружности, и выбор метода зависит от предпочтений и удобства. В этой статье мы рассмотрим несколько простых шагов, которые помогут вам эффективно решить задачу нахождения радиуса вписанной окружности в квадрат.
Как найти радиус вписанной окружности в квадрат
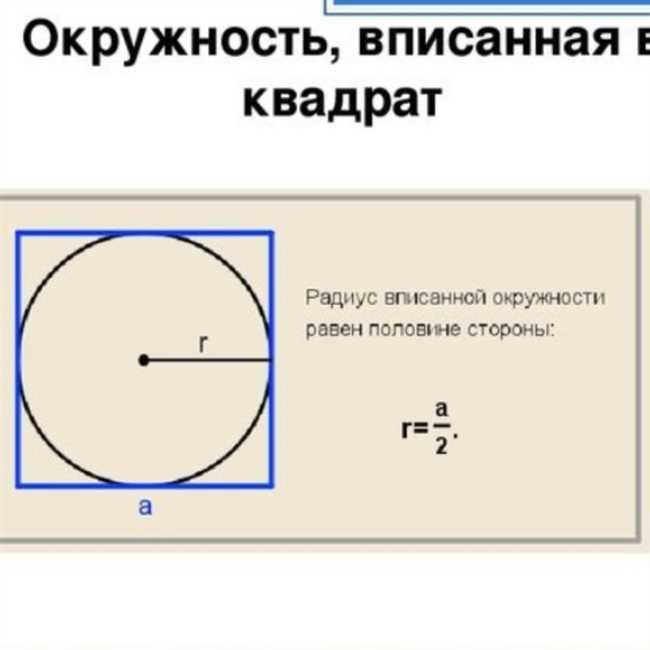
Давайте разберемся, как найти радиус вписанной окружности в квадрат. Для начала, вспомним некоторые свойства и определения. Квадрат — это прямоугольник, у которого все стороны равны между собой. Окружность — это множество точек, равноудаленных от центра. Итак, окружность вписана в квадрат, если ее центр находится в центре квадрата и при этом соприкасается со всеми сторонами.
Изучая эту задачу, можно заметить, что радиус вписанной окружности равен половине длины стороны квадрата. Это обусловлено тем, что окружность соприкасается со всеми сторонами квадрата и ее радиус равен расстоянию от центра до любой стороны.
Таким образом, чтобы найти радиус вписанной окружности в квадрат, нужно знать длину стороны квадрата и поделить ее на 2. Например, если сторона квадрата равна 10 см, то радиус вписанной окружности будет равен 10/2 = 5 см.
В случае, если вам известен диаметр окружности, вы можете найти радиус, разделив его на 2. Например, если диаметр равен 12 см, то радиус вписанной окружности будет равен 12/2 = 6 см.
Важно отметить, что радиус вписанной окружности не меняется при повороте квадрата. То есть, независимо от того, каким образом вы располагаете квадрат, радиус вписанной окружности будет оставаться постоянным.
Чтобы закрепить полученные знания, решите несколько задач самостоятельно. Например, найдите радиус вписанной окружности в квадрат со стороной 15 см.
Шаг 1: Постановка задачи
Итак, стоящая перед нами задача — найти радиус вписанной окружности в квадрат. Чтобы справиться с ней, нам потребуется знать несколько важных деталей. Во-первых, квадрат — это фигура, у которой все стороны равны между собой. Во-вторых, радиус вписанной окружности — это расстояние от центра окружности до любой ее точки.
Для того чтобы найти радиус вписанной окружности в квадрат, мы воспользуемся свойствами геометрической фигуры. Давайте разберемся, как именно это делается.
Шаг 2: Изучение свойств вписанной окружности
Теперь, когда мы разобрались с основами, пришло время углубиться в изучение свойств вписанной окружности в квадрате. Ответим на вопросы: какая связь между вписанной окружностью и квадратом? Какие свойства имеет такая окружность, и как мы можем использовать их для нахождения ее радиуса?
Первое, что нужно понять, это то, что вписанная окружность в квадрат касается его сторон в четырех точках. Это значит, что каждая сторона квадрата является касательной к окружности в точке соприкосновения. Более того, все касательные, проведенные из вершин квадрата до точек касания, имеют одинаковую длину.
Другое важное свойство вписанной окружности заключается в том, что отрезки, проведенные из центра окружности до точек касания со сторонами квадрата, являются радиусами. Это означает, что расстояние от центра окружности до точки касания равно радиусу окружности. Таким образом, для нахождения радиуса вписанной окружности в квадрат, нам нужно знать длину одного из отрезков, проведенных от центра окружности до точки касания.
Как же найти эту длину? Для этого мы можем использовать свойство равенства диагоналей квадрата. Диагонали квадрата являются его характеристической чертой, их длины равны друг другу. Если мы знаем длину одной из диагоналей, то можем использовать эту информацию для нахождения радиуса вписанной окружности. Мы можем найти длину диагонали, а затем разделить ее пополам, чтобы получить длину отрезка, проведенного из центра окружности до точки касания.
Пример:
Предположим, что у нас есть квадрат со стороной длиной 8 см. Нам нужно найти радиус вписанной окружности.
- Найдем длину одной из диагоналей. По теореме Пифагора, квадрат длины диагонали равен сумме квадратов длин сторон: $8^2 + 8^2 = 64 + 64 = 128$. Тогда длина диагонали равна $\sqrt{128} \approx 11.31$ см.
- Разделим длину диагонали пополам, чтобы найти длину отрезка, проведенного из центра окружности до точки касания. В нашем случае это будет $11.31 / 2 = 5.65$ см.
- По свойству вписанной окружности, этот отрезок является радиусом, поэтому радиус окружности равен 5.65 см.
Таким образом, радиус вписанной окружности в квадрат со стороной 8 см равен примерно 5.65 см.
Теперь у нас есть более детальное представление о свойствах вписанной окружности в квадрат и о способах нахождения ее радиуса. Это поможет нам расширить наши знания и продвинуться к следующему шагу в изучении этой темы.
Шаг 3: Методы нахождения радиуса
Теперь, когда мы поняли, чему равен периметр квадрата и как найти его, давайте обратимся к вопросу о нахождении радиуса вписанной окружности. В этом шаге мы рассмотрим несколько методов, которые позволят нам эффективно вычислить радиус.
1. Метод через диагонали квадрата: Если у вас есть информация о длине диагонали квадрата, вы можете использовать следующую формулу:
| Формула | Описание |
|---|---|
| Радиус = (диагональ квадрата) / 2 | Для квадрата с диагональю D радиус вписанной окружности будет равен половине длины диагонали. |
2. Метод через сторону квадрата: Если у вас есть информация о длине стороны квадрата, вы можете использовать следующую формулу:
| Формула | Описание |
|---|---|
| Радиус = (сторона квадрата) * sqrt(2) / 2 | Для квадрата со стороной S радиус вписанной окружности будет равен половине произведения длины стороны на корень из 2. |
3. Метод через площадь квадрата: Если у вас есть информация о площади квадрата, вы можете использовать следующую формулу:
| Формула | Описание |
|---|---|
| Радиус = sqrt(площадь квадрата) / 2 | Для квадрата с площадью A радиус вписанной окружности будет равен половине корня из площади. |
4. Метод через периметр квадрата: Если у вас есть информация о периметре квадрата, вы можете использовать следующую формулу:
| Формула | Описание |
|---|---|
| Радиус = (периметр квадрата) / (4 * sqrt(2)) | Для квадрата с периметром P радиус вписанной окружности будет равен четверти периметра, деленной на корень из 2. |
Возможно, вы уже заметили, что все эти методы используют разные формулы для нахождения радиуса вписанной окружности. Выбор метода зависит от того, какая информация у вас есть о квадрате.
Таким образом, мы рассмотрели четыре простых и эффективных метода нахождения радиуса вписанной окружности в квадрат. Вы можете выбрать подходящий метод в зависимости от доступной вам информации о квадрате. Уверены, что сейчас вам будет гораздо проще решать задачи, связанные с вычислением радиуса вписанной окружности в квадрате!
Шаг 4: Примеры задач и их решения
Рассмотрим несколько примеров задач, связанных с нахождением радиуса вписанной окружности в квадрат. Каждая задача будет сопровождаться подробным решением, чтобы вы могли лучше понять методы решения и применять их в собственной практике.
Пример 1:
Найдите радиус вписанной окружности в квадрат со стороной 6 см.
Решение:
Для решения этой задачи мы можем воспользоваться формулой для радиуса вписанной окружности в квадрат: радиус = половина длины стороны квадрата.
В нашем случае, длина стороны квадрата равна 6 см. Подставляем это значение в формулу:
радиус = 6 / 2 = 3 см
Пример 2:
Найдите радиус вписанной окружности в квадрат, если известна площадь квадрата равная 64 квадратных см.
Решение:
Для решения этой задачи мы можем воспользоваться формулой для площади квадрата, которая равна сторона квадрата в квадрате: площадь = сторона^2.
В нашем случае, площадь квадрата равна 64 квадратных см. Из этого значения можно найти сторону квадрата:
сторона = квадратный корень(площадь) = квадратный корень(64) = 8 см
Затем, чтобы найти радиус вписанной окружности, мы просто берем половину длины стороны квадрата:
радиус = 8 / 2 = 4 см
Таким образом, радиус вписанной окружности в квадрат со стороной 8 см равен 4 см.
Теперь вы знакомы с примерами задач и методами их решения по нахождению радиуса вписанной окружности в квадрат. Используйте эти знания в своих задачах и практике, чтобы совершенствовать свои навыки!






