
Если вам нужно найти радиус шара по его объему, то вы находитесь в правильном месте! В этой статье я расскажу вам, как сделать это, используя простые математические формулы. Во-первых, нужно знать формулу для вычисления объема шара, которая выглядит так: V = 4/3 * π * r³, где V — объем, а r — радиус шара.
Чтобы найти радиус, необходимо перевести уравнение в более простую форму, выражая радиус через объем: r = ³√(3V / (4π)). Теперь вы можете приступить к вычислениям! Подставьте известные значения и, используя калькулятор, найдите значение радиуса. Обратите внимание, что для этого вам потребуется знать значение числа π (пи), которое примерно равно 3,14159.
Итак, все готово для того, чтобы вы могли найти радиус шара по его объему. Следуйте инструкции и решайте математические задачи легко и быстро!
Шаг 1: Знакомство с формулой объема шара
Радиус шара — это расстояние от центра шара до любой точки на его поверхности. Формула для нахождения объема шара выглядит следующим образом:
V = (4/3)πr³
Здесь V — объем шара, π (пи) — математическая константа, примерное значение которой равно 3,14159, а r — радиус.
Теперь, когда мы знакомы с формулой, можем перейти к самому интересному — способу нахождения радиуса шара по заданному объему. Закрепи свой плащ, потому что мы собираемся отправиться в удивительный мир математики!
Что такое объем шара?
Радиус шара — это расстояние от центра шара до любой точки на его поверхности. Радиус является ключевым параметром в расчете объема шара, поскольку он определяет размеры шара. Изменение радиуса шара влияет на его объем.
Объем шара можно вычислить с использованием формулы:
Объем = (4/3) * π * R³
Где π (пи) равно приблизительно 3,14159. Данная формула используется для вычисления объема шара, если известен его радиус. Радиус указывается в кубических единицах, поскольку он возводится в куб при расчете объема.
Чтобы подробнее разобраться в вычислении объема шара по его радиусу, рассмотрим несколько практических примеров:
- Пример 1: Если радиус шара равен 5 сантиметрам, то вычислим его объем:
- Возводим радиус в куб: 5³ = 125
- Домножаем на (4/3) * π: (4/3) * 3,14159 * 125 ≈ 523,598
- Таким образом, объем шара с радиусом 5 сантиметров составляет приблизительно 523,6 кубических сантиметра.
- Пример 2: Предположим, что у нас имеется шар с объемом 1000 кубических метров. Найдем его радиус:
- Делим объем на (4/3) * π: 1000 / (4/3) * 3,14159 ≈ 238,734
- Извлекаем кубический корень: ∛238,734 ≈ 6,071
- Таким образом, радиус шара с объемом 1000 кубических метров равен приблизительно 6,071 метра.
Мы рассмотрели основные аспекты определения объема шара по его радиусу. Зная формулу и значение числа π, вы можете легко вычислить объем шара при заданном радиусе или наоборот.
Теперь, когда вы знаете, что такое объем шара, вы можете использовать эту информацию в разных областях, таких как строительство, архитектура, физика и т.д. Объем шара является важной концепцией в науке и позволяет нам лучше понять пространственные характеристики объектов. Надеюсь, эта информация была полезной для вас!
Какая формула используется для расчета объема шара?

Формула для расчета объема шара выглядит следующим образом:
V = (4/3)πr³
Где:
- V — объем шара;
- π — число пи, приближенное значение которого равно 3.14;
- r — радиус шара.
Для выполнения расчета верно запишите значения радиуса и используйте данную формулу. Также не забывайте уточнять единицы измерения, которые используются в условии задачи. Это поможет вам правильно интерпретировать результат расчета.
В. Разбор формулы на примере
Продолжая рассматривать тему «Как найти радиус шара по объему», мы можем разобрать формулу на примере для лучшего понимания. Радиус шара можно найти, зная его объем и используя специальную формулу.
Формула для нахождения радиуса шара по объему выглядит следующим образом:
r = ∛(3V / (4π))
где:
- r — радиус шара
- V — объем шара
- π — число пи (приближенное значение 3.14)
Давайте разберем эту формулу на конкретном примере.
Предположим, у нас есть шар с объемом 1000 кубических сантиметров. Найдем радиус этого шара, используя формулу.
Сначала вставим известные значения в формулу:
r = ∛(3 * 1000 / (4 * 3.14))
Далее произведем вычисления:
r = ∛(3000 / 12.56)
r = ∛239.23
r ≈ 6.2
Таким образом, радиус шара составляет примерно 6.2 сантиметра при объеме 1000 кубических сантиметров.
Теперь вы можете взять любой другой шар с известным объемом и использовать данную формулу, чтобы найти его радиус. Не забывайте заменить значение V в формуле на объем вашего шара и произвести необходимые вычисления.
Попробуйте применить эту формулу на практике и убедитесь, что можете сами найти радиус шара по его объему. Это простой способ определить размер шара, основываясь на его объеме.
Шаг 2: Определение значения объема шара
Итак, теперь, когда мы знаем формулу для расчета объема шара, давайте перейдем к определению значения объема.
Объем шара определяется по формуле:
V = (4/3) * π * r^3
Где:
- V — объем шара
- π (пи) — математическая константа, которая примерно равна 3.14159
- r — радиус шара
- ^3 — символ возвести число в куб
Теперь самое время использовать ваш объем из шага 1 и найти радиус шара. Давайте подставим значения в формулу и решим ее.
| Шаг 1: Значение объема шара | Шаг 2: Расчет радиуса шара |
|---|---|
| V = 1000 см³ | V = (4/3) * π * r^3 |
| 1000 = (4/3) * π * r^3 | |
| Теперь давайте избавимся от коэффициента (4/3), разделив обе стороны уравнения на него: | |
| 1000 / (4/3) = π * r^3 | |
| 750 = π * r^3 | |
| Теперь давайте избавимся от символа возвести число в куб, извлекая кубический корень из обеих сторон уравнения: | |
| ∛(750) = ∛(π * r^3) | |
| ∛(750) ≈ 8.66 | |
| Теперь подставим найденное значение радиуса обратно в формулу для радиуса шара: | |
| r ≈ 8.66 см |
Итак, радиус шара, при условии его объема равного 1000 см³, составляет примерно 8.66 см.
Теперь, когда у вас есть радиус шара, вы готовы перейти к третьему шагу, чтобы найти площадь поверхности шара.
А. Получение данных
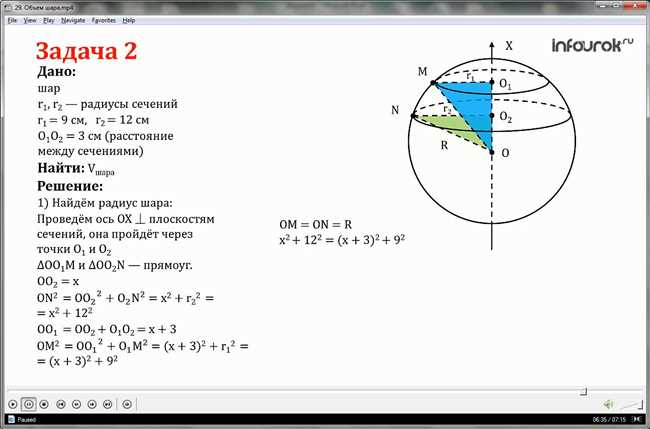
Чтобы рассчитать радиус шара по его объему, нам необходимо знать значение самого объема.
Вопрос: Какого объема шар вам нужно найти радиус?
Возможно, у вас есть шар и вы хотите узнать его радиус, или же вам известен только объем и вы хотите рассчитать радиус. В обоих случаях нам понадобятся некоторые известные данные.
Если у вас уже есть шар, то вам необходимо измерить его объем. Но как это сделать? Для этого вам потребуется специальный прибор, называемый «гидрометром». С его помощью вы сможете определить объем шара путем того, чтобы погрузить его в воду и измерить объем воды, вытесненный шаром. Таким образом, объем шара будет равен объему воды, вытесненной им.
Если вам известен только объем шара, то просто запишите его значение. Например, пусть вам известно, что объем шара равен 100 кубическим сантиметрам. В таком случае, вам не нужно измерять объем шара, так как он уже известен.
Теперь, когда у нас есть значение объема шара, мы можем перейти к следующему шагу — расчету радиуса. Поверьте, вы справитесь с этой задачей! Приступим к следующему шагу.
Заключение:
Б. Подстановка данных в формулу
В данной статье мы разобрали, как можно найти радиус шара по его объему. В основе этой задачи лежит формула объема шара, которая выглядит следующим образом:
V = (4/3)πr³
Чтобы найти радиус шара, необходимо подставить известные значения в эту формулу и решить уравнение относительно радиуса. Для этого следует:
- Записать известные данные, такие как значение объема шара и значение числа π.
- Подставить эти значения в формулу объема шара.
- Решить уравнение относительно радиуса.
- Получить значение радиуса шара.
Таким образом, используя формулу объема шара и подстановку данных, мы можем легко найти радиус шара по его объему. Эта простая и понятная методика позволяет решить задачу с небольшими усилиями.






