Как найти полупериметр треугольника простым способом расчета

Как найти полупериметр треугольника: простой способ расчета

Знание полупериметра треугольника является важным элементом для многих геометрических расчетов. Полупериметр представляет собой половину суммы длин всех его сторон. Расчет полупериметра треугольника — это простая задача, требующая только знания длин его сторон. Нет необходимости в специальных формулах или сложных вычислениях. Основополагающие математические принципы позволяют нам легко вычислить полупериметр треугольника. В этой статье я расскажу о простом способе расчета полупериметра треугольника и дам несколько примеров для лучшего понимания.

Определение полупериметра треугольника

Чтобы лучше понять этот термин, представьте, что у вас есть треугольник и вы хотите найти его полупериметр. Прежде всего, необходимо измерить длины всех трех сторон треугольника. Затем просто сложите эти значения и разделите на 2.

Например, если ваш треугольник имеет стороны длиной 6 см, 8 см и 10 см, то полупериметр будет равен (6 + 8 + 10) / 2 = 24 / 2 = 12 см.

Зачем нам нужен полупериметр треугольника? Есть несколько ситуаций и задач, в которых знание полупериметра может быть полезным.

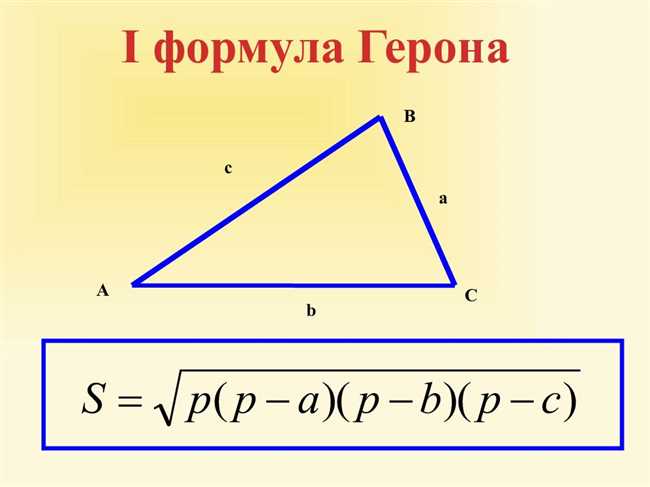
1. Расчет площади треугольника. Полупериметр является одним из компонентов формулы для расчета площади треугольника по формуле Герона. Формула Герона гласит: площадь треугольника = √(p * (p — a) * (p — b) * (p — c)), где p — полупериметр, а, b, c — длины сторон треугольника. Полупериметр позволяет упростить эту формулу и упростить расчет площади треугольника.
2. Проверка неравенства треугольника. Существует правило, согласно которому сумма длин любых двух сторон треугольника должна быть больше третьей стороны. Если полупериметр треугольника меньше самой длинной стороны, то это означает, что треугольник не может существовать. Это простой способ проверки правильности построения треугольника.
3. Расчет периметра треугольника. Полупериметр является половиной периметра треугольника. Поэтому если вы знаете полупериметр, вы можете легко найти полный периметр, удваив его значение.

Теперь, когда вы знаете, что такое полупериметр треугольника и зачем он используется, вы можете смело приступать к решению задач, связанных с этой темой. Я уверен, что вы справитесь с ними!

Что такое полупериметр треугольника?

Перед тем как я проложу путь непременного развития вашего знания, дайте мне задать вопрос: когда вы слышите слово «полупериметр», какие ассоциации у вас возникают? Я уверен, что многие из вас подумали о периметре, правильно? И это абсолютно нормально, ведь полупериметр и периметр тесно связаны между собой.

Теперь перейдем к основному вопросу: что же такое полупериметр треугольника? Для тех, кто только начинает свой путь в мир геометрии, полупериметр — это сумма длин всех сторон треугольника, деленная на 2. Просто представьте, что полупериметр — это центральный барьер, который дает вам возможность пройти к самомой глубине треугольника. Это величина, которая отвечает за его «полезность».

Но почему полупериметр, а не периметр? Отличный вопрос! Дело в том, что полупериметр представляет собой гармоничное сочетание простоты и эффективности. Полупериметр — это, по сути, половина от периметра, и это открывает перед нами массу возможностей для решения геометрических задач.

Может быть, сейчас вы задаетесь вопросом: «А зачем нам нужен полупериметр треугольника?» Ответ прост — с его помощью мы можем легко рассчитать другие важные величины, такие как площадь треугольника или его радиус вписанной окружности. Кроме того, полупериметр помогает нам классифицировать треугольники, распознавать их формы и свойства. Воистину универсальное понятие, не так ли?

Также стоит отметить, что полупериметр — это не просто сухая формула, изучение которой может вызвать огромное желание отвернуться и забыть. Нет! Полупериметр — это средство для понимания глубины треугольника, его сущности и потенциала. Ведь лишь зная полупериметр, мы можем на самом деле «увидеть» треугольник и его все особенности.

Итак, уважаемые друзья, полупериметр треугольника — это величина, которая помогает нам понять суть треугольника и использовать его свойства для решения различных задач. Она является центральной фигурой в мире геометрии, открывая перед нами двери к новому знанию и пониманию. Поэтому не бойтесь полупериметра, а откройте перед собой его потенциал и впускайте свет знаний в свои головы!

Простой способ расчета полупериметра

Как же вычислить полупериметр треугольника? Для начала необходимо знать длины всех его сторон. Пусть у нас есть треугольник со сторонами a, b и c. Тогда полупериметр можно вычислить по формуле:

p = (a + b + c) / 2

Давайте рассмотрим пример. Предположим, что у нас есть треугольник со сторонами длиной 5, 7 и 9.

Для начала, сложим длины всех сторон:

• 5 + 7 + 9 = 21

Затем разделим полученную сумму на 2:

• 21 / 2 = 10.5

Таким образом, полупериметр этого треугольника равен 10.5.

И это все! Теперь вы знаете простой способ расчета полупериметра треугольника. Помните, что полупериметр может быть использован для решения множества задач, связанных с треугольниками, поэтому это очень полезная формула, которую стоит запомнить.

Как получить длины сторон треугольника?

У каждого треугольника есть три стороны, и чтобы решать задачи, связанные с треугольниками, нам нужно знать длины этих сторон. Но как мы можем получить эти значения? Давайте разберемся в этом вопросе и узнаем, как определить длины сторон треугольника.

Существует несколько способов, которые могут помочь нам получить длины сторон треугольника:

• Используйте известные данные. Если в задаче уже известны некоторые данные о треугольнике, например, его площадь или высота, то вы можете использовать эти данные для определения длины сторон. Например, если известна площадь треугольника и одна из его сторон, вы можете использовать формулу для расчета длины другой стороны.
• Примените теорему Пифагора. Если треугольник является прямоугольным, вы можете использовать теорему Пифагора для определения длины сторон. Теорема Пифагора гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов. Таким образом, если известны длины двух сторон треугольника, и одна из них является гипотенузой, вы можете использовать теорему для определения длины другой стороны.
• Используйте тригонометрические соотношения. Если известны углы треугольника и одна из длин сторон, вы можете использовать тригонометрические функции (синус, косинус, тангенс) для определения длины других сторон. Например, если известны угол треугольника и длины двух сторон, вы можете использовать тангенс угла и формулу для определения длины третьей стороны.

Зная эти методы, вы сможете легко определить длины сторон треугольника. Это очень полезные навыки, которые могут пригодиться во многих различных областях, таких как геометрия, физика и инженерия.

Так что, следующий раз, когда у вас будет задача, связанная с треугольниками, не паникуйте! Просто примените эти методы и вы сможете получить длины сторон треугольника без проблем.

Формула для расчета полупериметра треугольника

Первым шагом является определение длин сторон треугольника. Для этого вы можете измерить каждую сторону с помощью линейки или использовать известные значения, если они имеются. Обозначим эти стороны как a, b и c.

После получения длин сторон треугольника, можно приступить к расчету полупериметра. Формула для его расчета выглядит следующим образом:

полупериметр = (a + b + c) / 2

В этой формуле мы просто суммируем длины всех сторон и делим полученное значение на два.

Возможно, вы задаетесь вопросом, зачем нам нужен полупериметр треугольника? Ответ прост: он является ключевым параметром для решения множества геометрических задач, связанных с треугольниками. Например, полупериметр используется при расчете площади треугольника по формуле Герона.

Когда вы знаете значение полупериметра, вы можете использовать его для решения различных задач, связанных с треугольником. Например, вы можете рассчитать площадь треугольника, периметр треугольника или определить, является ли треугольник прямоугольным или равносторонним.

Таким образом, формула для расчета полупериметра треугольника имеет большое практическое значение и может быть использована для решения различных задач. Не стесняйтесь применять ее в своих математических расчетах и убедитесь, что вы правильно выполнили все шаги.

1. Необходимо определить длины сторон треугольника.
2. Вычислить полупериметр треугольника, применив формулу: полупериметр = (a + b + c) / 2.
3. Используйте значение полупериметра для решения задач, связанных с треугольником, включая вычисление площади треугольника, периметра треугольника и проверку, является ли треугольник прямоугольным или равносторонним.

Как использовать формулу для расчета полупериметра?

Перед тем, как погрузиться в формулы и математические выкладки, давайте рассмотрим, что такое полупериметр треугольника. Полупериметр (иногда обозначается как s) — это сумма всех сторон треугольника, деленная на 2. Формула для расчета полупериметра треугольника выглядит следующим образом:

s = (a + b + c) / 2

Где a, b и c — длины сторон треугольника. Определить значения a, b и c можно, измерив их с помощью линейки или другого измерительного инструмента.

Теперь, когда у нас есть формула, давайте посмотрим на пример, чтобы лучше разобраться в ее использовании. Представим, что у нас есть треугольник, у которого стороны равны a = 5, b = 7 и c = 9. Мы можем использовать формулу для расчета полупериметра:

s = (5 + 7 + 9) / 2

Подставим значения в формулу:

s = 21 / 2

Теперь проведем деление:

s = 10.5

Итак, полупериметр нашего треугольника равен 10.5.

Теперь у нас есть готовый ответ на вопрос «Как использовать формулу для расчета полупериметра?». Этот простой математический инструмент может быть очень полезным в различных ситуациях, где нужно знать и использовать размеры сторон треугольника. Не стесняйтесь применять эту формулу для расчета полупериметра и наслаждайтесь результатами!

Примеры расчета полупериметра треугольника

Пример 1: Прямоугольный треугольник

Предположим, у вас есть прямоугольный треугольник с катетами a = 5 и b = 12. Вы хотите найти его полупериметр. Как это сделать? Очень просто!

Сначала нужно найти гипотенузу треугольника, используя теорему Пифагора. Для прямоугольного треугольника формула будет следующей:

c = √(a² + b²)

Следовательно, в нашем случае:

c = √(5² + 12²)

c = √(25 + 144)

c = √(169)

c = 13

Теперь, когда у нас есть все стороны треугольника, можем найти его полупериметр по формуле:

p = (a + b + c) / 2

Возвращаемся к нашему примеру:

p = (5 + 12 + 13) / 2

p = 30 / 2

p = 15

Итак, полупериметр нашего прямоугольного треугольника равен 15.

Пример 2: Равносторонний треугольник

Давайте рассмотрим теперь равносторонний треугольник со стороной a = 8. Найдем его полупериметр.

Так как у нас равносторонний треугольник, все его стороны равны друг другу. Поэтому просто умножаем сторону на 3:

p = a * 3

Возвращаемся к нашему примеру:

p = 8 * 3

p = 24

Итак, полупериметр равностороннего треугольника со стороной 8 равен 24.

Вот и все примеры расчета полупериметра треугольника! Надеюсь, они помогли вам лучше понять эту концепцию и как применять ее на практике. Я уверен, что теперь вы сможете успешно рассчитать полупериметр любого треугольника, с которым столкнетесь. Удачи вам!

Пример 1: Расчет полупериметра для треугольника со сторонами 5, 7 и 9

В данном примере треугольник имеет стороны длиной 5, 7 и 9. Используя формулу, мы можем легко рассчитать полупериметр:

Сумма всех сторон треугольника равна 5 + 7 + 9 = 21. Делим полученную сумму на 2:

s = (5 + 7 + 9) / 2 = 21 / 2 = 10.5

Таким образом, полупериметр треугольника со сторонами 5, 7 и 9 равен 10.5.