Как найти площадь треугольника в 4 классе: простое объяснение и примеры

Если ты учится в 4 классе и хочешь узнать, как найти площадь треугольника, то ты попал в нужное место! Решать эту задачу несложно, и я объясню тебе, как это сделать.

Для начала, нам потребуется знать длины двух сторон треугольника. Они могут быть разными, но обязательно знай их значения. Затем мы найдем высоту – это перпендикуляр, проведенный из одного угла треугольника к противоположной стороне. Когда мы знаем длину стороны и соответствующую ей высоту, мы можем применить простую формулу для вычисления площади треугольника.

Чтобы разобраться еще лучше, давай посмотрим на примере. Представь, что у нас есть треугольник со сторонами длиной 5 см, 7 см и 9 см. Найдем высоту, проведя перпендикуляр к стороне длиной 9 см. Затем, подставим значения в формулу и найдем площадь треугольника. Просто, правда?

Что такое площадь треугольника?

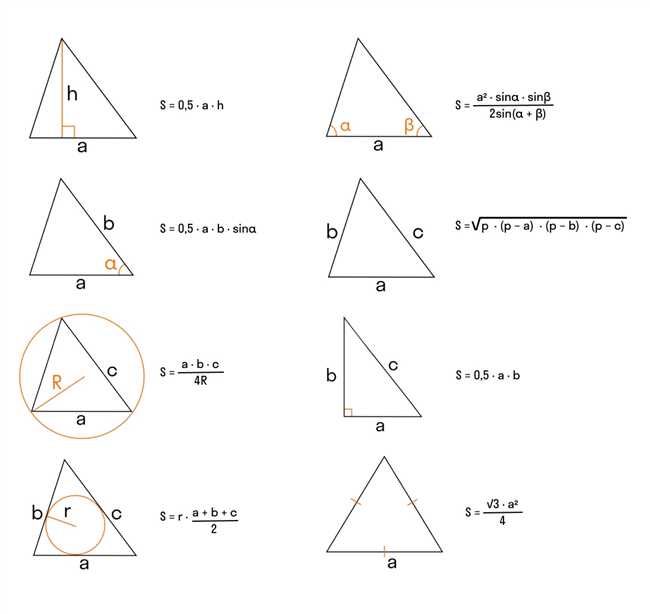
Вы уже наверняка знаете, что треугольник имеет три стороны и три угла. Один из способов найти площадь треугольника — это умножить длину одной стороны на длину высоты, опущенной на эту сторону. Высота треугольника — это линия, проведенная перпендикулярно выбранной стороне и проходящая через противоположный угол.

Но что делать, если у вас нет данных о высоте треугольника? Не волнуйтесь, есть другие способы найти площадь треугольника. Если вы знаете длину двух сторон и угол между ними (называемый векторным произведением), то можно воспользоваться формулой:

Площадь = (a * b * sin(угол между сторонами)) / 2

Где a и b — длины сторон треугольника. Используя эту формулу, вы сможете найти площадь треугольника без знания высоты.

Иногда треугольник бывает равносторонним, то есть все его стороны равны между собой. В этом случае площадь треугольника можно вычислить с помощью формулы:

Площадь = (a^2 * √3) / 4

Где a — длина стороны треугольника.

Округляя числа или переводя их в десятичные значения, вы получите результат — площадь треугольника.

Теперь, когда вы знаете, что такое площадь треугольника и как ее найти, попробуйте применить эти знания на практике. Вы можете взять лист бумаги и линейку, чтобы нарисовать свой собственный треугольник и вычислить его площадь. Также можно попросить учителя или родителей придумать интересные примеры, чтобы потренироваться в расчете площади треугольника.

Удачи в изучении площади треугольника!

Формула для вычисления площади треугольника

Вы, наверное, уже слышали о треугольниках и знаете, что это многоугольник с тремя сторонами. Но знали ли вы, что у него также есть площадь? Давайте поговорим о том, как можно вычислить площадь треугольника!

Формула для вычисления площади треугольника зависит от его основания и высоты. Основание — это одна из его сторон, а высота — перпендикулярная прямая, опущенная из вершины к основанию.

Вот самая простая формула для вычисления площади треугольника:

S = (основание * высота) / 2

Теперь давайте посмотрим на пример. Предположим, у нас есть треугольник с основанием длиной 4 сантиметра и высотой 2 сантиметра. Чтобы вычислить его площадь, мы можем использовать формулу:

S = (4 * 2) / 2 = 8 / 2 = 4

Таким образом, площадь этого треугольника равна 4 квадратным сантиметрам.

Теперь вы можете с легкостью вычислить площадь треугольника! Просто найдите основание и высоту, подставьте их в формулу и вы получите ответ. Попробуйте посчитать площадь треугольника сами, задав основание и высоту!

И помните, площадь — это важное понятие в геометрии, она помогает нам измерять поверхность треугольника и многие другие фигуры. Но главное — практикуйтесь, и вы сможете легко вычислять площади треугольников и других фигур без формулы!

Примеры вычисления площади треугольника

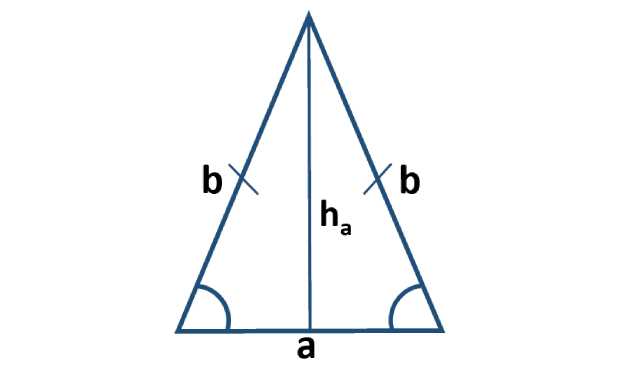
Пример 1: Пусть у нас есть треугольник с основанием 5 см и высотой 4 см. Какова его площадь?

Чтобы найти площадь треугольника, мы можем воспользоваться формулой: «Площадь треугольника равна половине произведения его основания и высоты». Применим эту формулу к нашему примеру:

Площадь = 1/2 × основание × высота

Площадь = 1/2 × 5 см × 4 см

Площадь = 10 см²

Таким образом, площадь треугольника с основанием 5 см и высотой 4 см равна 10 см².

Пример 2: Измерение основания и высоты треугольника может быть немного сложнее в реальной жизни, но мы всегда можем использовать линейку или другие инструменты для получения точных значений. Давайте представим треугольник со сторонами 6 см, 8 см и 10 см. Как найти его площадь?

Мы можем использовать формулу герона, которая позволяет нам найти площадь треугольника, зная длины его сторон. Формула герона выглядит следующим образом:

Площадь = √(p × (p — a) × (p — b) × (p — c))

Где p – полупериметр треугольника (p = (a + b + c)/2)

Применяя формулу герона к нашему примеру:

p = (6 см + 8 см + 10 см)/2 = 12 см

Площадь = √(12 см × (12 см — 6 см) × (12 см — 8 см) × (12 см — 10 см))

Площадь = √(12 см × 6 см × 4 см × 2 см)

Площадь = √(576 см²)

Площадь ≈ 24 см²

Итак, площадь треугольника со сторонами 6 см, 8 см и 10 см, равна примерно 24 см².

Таким образом, вычисление площади треугольника — это увлекательный процесс, который можно легко овладеть, применяя соответствующие формулы и используя правильные значения основания и высоты или длины его сторон. Практикуйтесь в решении задач и наслаждайтесь математикой!

Интерактивная игра для тренировки вычисления площади треугольника

Вы уже знаете, что площадь треугольника можно найти, умножив длину основания на высоту и разделив полученное значение на 2. Но вам нужно научиться применять эту формулу в практике, и мы вам поможем!

Для этой цели мы создали интерактивную игру, в которой вы будете тренироваться в вычислении площади треугольника. Вам потребуется набрать определенное количество очков, решая задачи на вычисление площади треугольников. Каждая задача будет немного отличаться от предыдущей, чтобы вы могли лучше понять, как применять формулу.

После завершения каждой задачи вы получите обратную связь о том, правильно ли вы рассчитали площадь или нет. Если вы ответили верно, ваш счет будет увеличен на определенное количество очков. Если вы допустили ошибку, вы сможете попробовать решить задачу еще раз.

Игра позволит вам улучшить свои навыки в вычислении площади треугольника и укрепит вашу уверенность в своих математических способностях. Вы сможете применять эти навыки в повседневной жизни, например, для расчета площади участка на земле или поверхности комнаты.

Не бойтесь совершать ошибки! Игра предназначена для тренировки, поэтому ваша задача — не только правильно рассчитать площадь, но и понять, что вы сделали неправильно, если ваш ответ оказался неверным. Это поможет вам научиться избегать ошибок в будущем и стать лучшим в расчете площади треугольника!

Итак, готовы начать игру? Приступайте к решению задач и постарайтесь набрать максимальное количество очков! Удачи!

Полезные советы и трюки для вычисления площади треугольника

Найдя площадь треугольника, мы можем узнать, сколько площади занимает эта фигура на плоскости. Правильное вычисление площади треугольника может быть полезно в различных задачах, таких как строительство или геометрические расчеты. В этой статье мы поделимся полезными советами и трюками для вычисления площади треугольника.

1. Формула для вычисления площади треугольника

Обычно, чтобы найти площадь треугольника, мы используем формулу:

S = 0.5 * a * h, где S — площадь, a — длина основания треугольника, h — высота, опущенная на основание.

2. Приложения для вычисления площади треугольника

В современном мире, есть множество приложений и онлайн-калькуляторов, которые могут помочь вам вычислить площадь треугольника быстро и безошибочно. Некоторые из них могут быть полезными для учеников и учителей, чтобы упростить процесс обучения и вычисления.

3. Различные методы для вычисления площади треугольника

Существуют разные методы для вычисления площади треугольника, в зависимости от доступной информации о фигуре. Некоторые из них включают использование формулы герона, формулы площади по трем сторонам и углу, метода полусуммы или разности площадей треугольников, и других.

4. Примеры практического использования вычисления площади треугольника

Найденная площадь треугольника может быть использована для различных практических целей. Например, при строительстве зданий, треугольные фишки или трафареты могут быть использованы для вырезания треугольной крыши или оконной рамы. Также, площадь треугольника может использоваться для расчета затрат на краску или пол, при планировании расстановки мебели, или для вычисления объема материала, необходимого для конкретного проекта.

• 5. Регулярная практика
• 6. Коллективное решение
• 7. Обмен опытом

Вычисление площади треугольника может быть довольно простым, если вы овладеете основными методами и правильно их примените. Практика и обмен опытом с другими людьми могут помочь улучшить ваши навыки и позволить успешно решать задачи, связанные с вычислением площади треугольника. Не стесняйтесь использовать перечисленные выше советы и трюки, чтобы упростить процесс и получить точные результаты.