
Когда речь заходит о вычислении площади прямоугольной трапеции, необходимо знать верные формулы и правила. Прямоугольная трапеция имеет две параллельные стороны, из которых одна короче другой, и все углы 90°. Основным инструментом для вычисления площади является соответствующая формула: S = (a + b) × h ÷ 2, где a и b — длины оснований, h — высота трапеции.
Для лучшего понимания применения этой формулы в практике помогут примеры вычисления площади. Например, если основание a равно 6 см, основание b равно 10 см, а высота h равна 4 см, подставляя значения в формулу, получаем: S = (6 + 10) × 4 ÷ 2 = 16 см². Таким образом, площадь прямоугольной трапеции равна 16 квадратным сантиметрам.
Определение прямоугольной трапеции
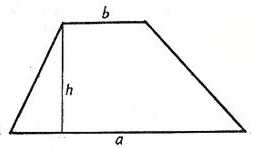
Прямоугольная трапеция имеет несколько важных элементов:
- Основания: две параллельные стороны, одна из которых длиннее другой.
- Высота: перпендикуляр от одного основания до другого. Высота является перпендикулярным отрезком, соединяющим стороны прямого угла, и образует угол 90 градусов с каждым основанием.
- Боковые стороны: остальные две стороны, не являющиеся основаниями.
Пример:
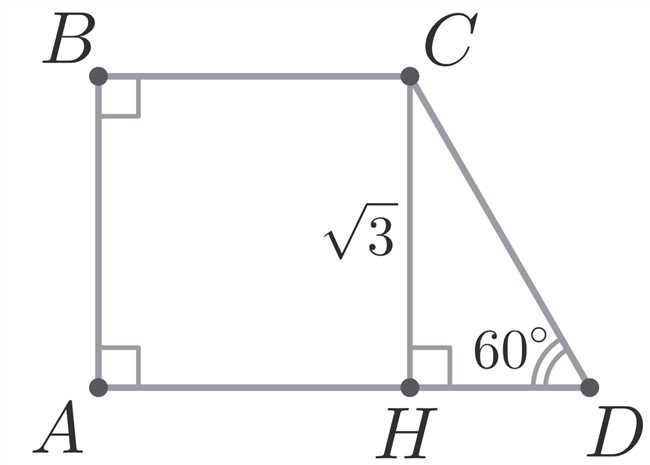
Представим, что у нас есть прямоугольная трапеция с основаниями длинной 10 см и 5 см, а высота равна 4 см.
Мы можем использовать формулу для расчета площади прямоугольной трапеции:
Площадь = (сумма оснований * высота) / 2
В нашем примере:
Площадь = (10 + 5) * 4 / 2 = 15 * 4 / 2 = 60 / 2 = 30
Таким образом, площадь нашей прямоугольной трапеции равна 30 квадратным сантиметрам.
Как вы можете видеть, знания о прямоугольной трапеции и формула для расчета ее площади могут быть очень полезными в различных ситуациях, например, при проектировании зданий, решении геометрических задач или построении различных фигур.
Формула для вычисления площади
Если вам нужно вычислить площадь прямоугольной трапеции, вам понадобится следующая формула:
S = (a + b) * h / 2
Где:
- a и b — длины оснований трапеции
- h — высота трапеции (расстояние между основаниями)
- S — площадь трапеции.
Вам нужно знать значения a, b и h, чтобы использовать эту формулу и вычислить площадь трапеции. Как только вы знаете эти значения, всего лишь подставьте их в формулу и выполните несколько математических операций.
Давайте рассмотрим пример, чтобы лучше понять, как использовать формулу:
Предположим, что у нас есть прямоугольная трапеция, у которой одно основание равно 6, а другое основание равно 10. В качестве высоты имеется 4. Мы хотим найти площадь этой трапеции.
В первую очередь, заменяем а и b на 6 и 10:
S = (6 + 10) * h / 2
Далее, заменяем h на 4:
S = (6 + 10) * 4 / 2
Затем, выполняем операции:
S = 16 * 4 / 2
S = 64 / 2
S = 32
Таким образом, площадь этой прямоугольной трапеции равна 32 единицам площади.
Теперь вы знаете формулу и можете легко вычислить площадь прямоугольной трапеции для любых значений оснований и высоты. Просто не забывайте подставить значения в формулу и выполнить необходимые математические операции.
Пример вычисления площади прямоугольной трапеции
Давайте рассмотрим пример вычисления площади прямоугольной трапеции. Представьте себе, что у вас есть трапеция с основаниями A и B, и вы хотите найти ее площадь.
Важно помнить, что формула для вычисления площади прямоугольной трапеции выглядит так: S = (a + b) * h / 2, где a и b — длины оснований, а h — высота трапеции.
Допустим, что у нас есть трапеция с основаниями A = 8 см и B = 12 см, а высота h = 5 см. Нам нужно найти ее площадь.
Подставляя значения в формулу, получаем:
S = (8 + 12) * 5 / 2 = 20 * 5 / 2 = 100 / 2 = 50 см²
Таким образом, площадь прямоугольной трапеции с заданными значениями оснований и высоты равна 50 квадратным сантиметрам.
Надеюсь, этот пример помог вам понять, как вычислять площадь прямоугольной трапеции. Есть ли у вас еще вопросы? Что-то еще, что я могу помочь вам выяснить? Дайте знать, и я буду рад помочь!
Заключение
Итак, мы рассмотрели формулу для вычисления площади прямоугольной трапеции и познакомились с примерами ее применения в практических задачах. Надеюсь, теперь вы уверенно сможете рассчитывать площадь данной геометрической фигуры.
Важно помнить, что формула не является единственным способом решения задачи. Иногда можно использовать иные методы, например, разбиение трапеции на прямоугольники или применение связанных геометрических фигур. Главное – понимать суть задачи и применять соответствующий метод решения.
Надеюсь, эта статья была полезной для вас и помогла вам разобраться с применением формулы для вычисления площади прямоугольной трапеции в практике. Удачи в решении ваших задач!






