
Часто возникает необходимость найти площадь прямоугольника, зная его периметр и диагональ. Это весьма полезный навык, который может пригодиться как в повседневной жизни, так и при решении математических задач.
Существует несколько методов для нахождения площади прямоугольника с заданными параметрами. Один из них — использование формулы, основанной на известных свойствах прямоугольника и теореме Пифагора. Другой метод — разбиение прямоугольника на два треугольника и нахождение их площадей.
В данной подробной инструкции мы рассмотрим оба метода и дадим пошаговые указания для решения задачи. При этом мы будем использовать простые математические выкладки и легко понятные объяснения, чтобы каждый мог успешно справиться со стоящей перед ним задачей.
Определение известных величин

Перейдем к определению известных величин, необходимых для решения задачи по нахождению площади прямоугольника с заданным периметром и диагональю.
Периметр прямоугольника – это сумма длин всех его сторон. Обычно обозначается латинской буквой «P». В задаче, для которой мы ищем решение, периметр уже задан и является известной величиной.
Диагональ прямоугольника – это прямая линия, соединяющая две противоположные вершины прямоугольника. Обозначается буквой «d». В задаче, для которой мы ищем решение, диагональ также уже задана и является известной величиной.
Также нам известна формула для нахождения площади прямоугольника, которая гласит: «Площадь прямоугольника равна произведению длин его сторон» или «S = a * b», где «S» – площадь, «a» и «b» – длины сторон. В нашем случае одна из сторон будет равна диагонали, а другая – периметру минус удвоенная длина стороны, соответствующей диагонали. Учитывая это, формула для нахождения площади будет выглядеть следующим образом: «S = (P — 2d) * d/2».
Нахождение сторон прямоугольника
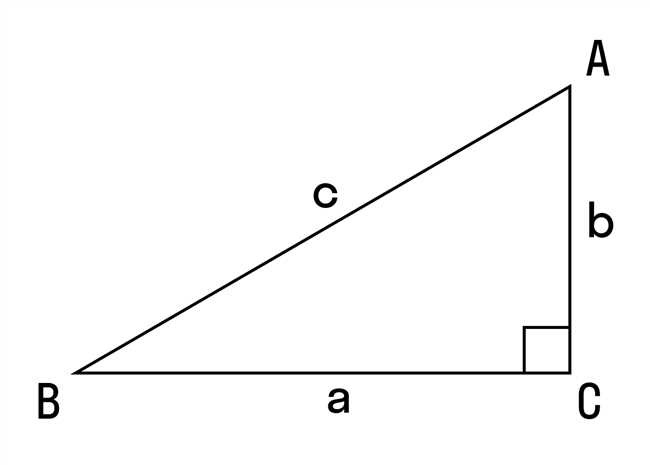
Нахождение сторон прямоугольника может показаться сложной задачей, но на самом деле это довольно просто. В этой статье мы рассмотрим несколько методов, которые помогут вам найти стороны прямоугольника, и вы сможете легко справиться с этой задачей.
Первый метод состоит в использовании периметра прямоугольника. Если у вас есть информация о периметре прямоугольника, вы можете использовать следующую формулу:
P = 2(a + b),
где P — периметр, a и b — стороны прямоугольника.
Вы можете использовать эту формулу, чтобы сначала найти сумму сторон прямоугольника, а затем разделить эту сумму пополам, чтобы найти каждую сторону в отдельности.
Еще один метод — использование диагонали прямоугольника. Если у вас есть информация о диагонали прямоугольника, вы можете использовать следующую формулу:
d2 = a2 + b2,
где d — диагональ, a и b — стороны прямоугольника.
Используя эту формулу, вы можете сначала найти квадраты сторон прямоугольника, затем сложить их, а затем извлечь квадратный корень для нахождения каждой стороны в отдельности.
Также можно использовать комбинированный метод, используя информацию о периметре и диагонали прямоугольника. Если у вас есть информация о периметре и диагонали, вы можете использовать следующие формулы:
P = 2(a + b),
d2 = a2 + b2.
Используя эти формулы, вы можете сначала найти сумму сторон прямоугольника, а затем, используя информацию о диагонали, вычислить значения сторон.
Приведенные выше методы помогут вам легко найти стороны прямоугольника, используя периметр и диагональ. Вы можете выбрать тот, который вам больше нравится или подходит в вашей конкретной ситуации. И не забывайте, что нахождение сторон прямоугольника — это важный шаг для решения многих задач, связанных с этой геометрической фигурой.
Нахождение площади прямоугольника
Шаг 1: Нахождение сторон прямоугольника
Периметр прямоугольника равен сумме длин всех его сторон, то есть: P = 2a + 2b, где a и b — стороны прямоугольника. Из этого уравнения можно выразить одну сторону через другую: a = (P — 2b) / 2. Теперь нужно найти такие значения сторон a и b, чтобы диагональ прямоугольника равнялась d.
Шаг 2: Нахождение длины диагонали
Диагональ прямоугольника связана со сторонами формулой Пифагора: d^2 = a^2 + b^2, где d — диагональ, a и b — стороны прямоугольника. Подставим значение a из первого шага в эту формулу: (P — 2b)^2/4 + b^2 = d^2. Решая это квадратное уравнение относительно b, можно найти значения сторон a и b.
Шаг 3: Нахождение площади прямоугольника
После того, как найдены значения сторон a и b, можно легко найти площадь прямоугольника, умножив их длины: S = a * b.
Просто, не правда ли? Но не забывайте, что для точного решения необходимо использовать правильные значения периметра и диагонали, а также правильные математические формулы. В случае сложностей или вопросов, всегда можно обратиться к учителю или математическому помощнику. Удачи в нахождении площади прямоугольника!
Заключение
В этой статье мы рассмотрели подробную инструкцию о том, как найти площадь прямоугольника при известном периметре и диагонали. Мы изучили математические формулы и шаг за шагом разобрали примеры расчетов.
Важно помнить, что для нахождения площади прямоугольника необходимо знать его периметр и диагональ. С использованием этих данных можно применить соответствующие формулы и получить точный результат. Расчеты могут быть полезны в различных сферах, например, для строительства или дизайна.
Надеемся, что данная статья была полезной и помогла вам разобраться в процессе нахождения площади прямоугольника с заданным периметром и диагональю. Если у вас остались вопросы или вы хотите узнать больше, не стесняйтесь обращаться к специалистам в данной области. Удачных вам расчетов и успешного применения полученных знаний!






