Когда речь идет о вычислении площади прямоугольника на клетчатой бумаге, существует несколько методов, которые помогут вам решить эту задачу. Один из наиболее простых и понятных методов – это подсчет количества квадратных клеток, которые охватывают прямоугольник. Для этого необходимо определить количество клеток по длине и ширине прямоугольника и умножить эти числа. Но существует и другой метод, основанный на понятии периметра и соотношении сторон прямоугольника. Он заключается в том, что площадь прямоугольника равна произведению его длины и ширины. Рассмотрим несколько примеров, чтобы лучше понять, как применять эти методы на практике.
Методы нахождения площади прямоугольника на клетчатой бумаге
Нахождение площади прямоугольника на клетчатой бумаге может показаться сложной задачей, но на самом деле существует несколько простых и надежных методов, которые помогут вам справиться с этой задачей. В этой статье мы рассмотрим несколько таких методов и предоставим примеры их использования.
Метод 1: Счет клеток
Самым простым способом нахождения площади прямоугольника на клетчатой бумаге является метод подсчета клеток. Сначала необходимо определить длину и ширину прямоугольника в клетках. Затем умножьте эти значения, чтобы получить итоговую площадь. Например, если длина прямоугольника составляет 5 клеток, а ширина 3 клетки, то площадь будет равна 5 * 3 = 15 клеток.
Пример:
| Длина | Ширина | Площадь |
|---|---|---|
| 5 клеток | 3 клетки | 15 клеток |
| 7 клеток | 4 клетки | 28 клеток |
Метод 2: Использование формулы
Другим методом нахождения площади прямоугольника на клетчатой бумаге является использование простой формулы. Формула для нахождения площади прямоугольника звучит следующим образом: площадь = длина * ширина. Этот метод особенно удобен, когда у вас есть прямоугольник со сторонами, заданными в единицах измерения длины, и нужно определить его площадь на клетчатой бумаге.
Пример:
| Длина | Ширина | Площадь |
|---|---|---|
| 7 см | 3 см | 21 клетка |
| 10 см | 5 см | 50 клеток |
- Подсчет клеток и использование формулы — это два простых и надежных метода нахождения площади прямоугольника на клетчатой бумаге.
- Необходимо определить длину и ширину прямоугольника в клетках или величинах длины, а затем умножить их, чтобы получить итоговую площадь.
- Перед началом работы убедитесь, что ваша клетчатая бумага соответствует единицам измерения длины, которые вы используете.
Вопрос: Какой метод нахождения площади вы предпочитаете использовать, подсчет клеток или использование формулы? Это зависит от ваших личных предпочтений и условий задачи. В случае, когда у вас есть точные измерения величин длины и ширины прямоугольника, использование формулы может быть более удобным и точным методом. Однако, подсчет клеток легче и может быть полезен при приближенных измерениях или в случае, когда нет возможности использования формулы.
Метод 1: Подсчет клеток
Для начала, нужно разместить прямоугольник на клетчатой бумаге таким образом, чтобы его стороны были параллельны линиям клеток. Затем, просто посчитайте количество целых клеток, на которые попадает прямоугольник.
Например, предположим, что у нас есть прямоугольник со сторонами 4 клетки и 6 клеток. Мы можем просто посчитать все клетки, на которых сосредоточен прямоугольник: 4 стороны, каждая соответствует 6 клеткам, в итоге получается 4 * 6 = 24 клетки.
Если вам сложно оценить количество клеток на стороне прямоугольника, вы можете использовать дополнительные шаги для упрощения задачи. Например, вы можете разделить прямоугольник на несколько более мелких частей, посчитать количество клеток в каждой части и затем сложить их вместе.
Этот метод особенно удобен, когда прямоугольник имеет нестандартную форму или когда его стороны не выровнены с линиями клеток. В этом случае, вы можете дополнительно поделить прямоугольник на более мелкие клетки для удобства подсчета.
Метод 2: Использование формулы
Если вы хотите вычислить площадь прямоугольника на клетчатой бумаге, вы можете использовать формулу, которая считывает количество клеток внутри прямоугольной фигуры.
Для начала, обратите внимание на ваш прямоугольник на клетчатой бумаге. Сколько клеток находится вдоль его длины и ширины? Представьте себе, что каждая клетка становится отдельным элементом, и насчитайте их все. Запишите количество клеток вдоль длины прямоугольника и количество клеток вдоль его ширины.
Например, представьте, что у вас есть прямоугольник размером 5 клеток вдоль длины и 3 клетки вдоль ширины. Запишите это: длина = 5, ширина = 3.
Затем, используя формулу для вычисления площади прямоугольника, умножьте длину на ширину.
Вернемся к нашему примеру: длина = 5, ширина = 3. Умножим их: 5 * 3 = 15.
Получается, площадь прямоугольника на клетчатой бумаге равна 15 клеткам.
Не забывайте, что каждая клетка на клетчатой бумаге является единичным элементом площади. Поэтому, когда вы считаете количество клеток вдоль длины и ширины прямоугольника, вы считаете количество единичных элементов площади и получаете итоговую площадь.
Таким образом, метод использования формулы является достаточно простым и эффективным способом вычислить площадь прямоугольника на клетчатой бумаге. Он позволяет вам быстро и точно определить площадь любого прямоугольника, используя только длину и ширину.
Примеры
В данной статье мы рассмотрели различные методы для вычисления площади прямоугольника на клетчатой бумаге. Познакомились с методом подсчета клеток, методом сравнения площадей фигур, а также методом разбиения прямоугольника на дополнительные фигуры.
Для наглядности и лучшего понимания приведены примеры на каждый из методов. Мы рассмотрели как находить площадь прямоугольника, используя каждый из методов, а также провели сравнение результатов. Это помогло убедиться в правильности применения каждого метода и выбрать наиболее удобный и точный способ вычисления площади прямоугольника на клетчатой бумаге.
Пример 1: Метод подсчета клеток
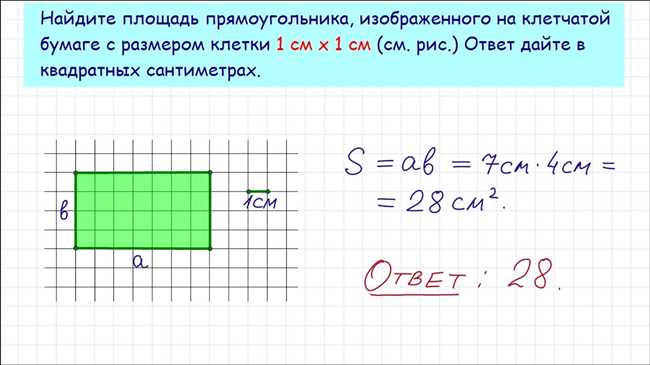
Рассмотрим прямоугольник со сторонами 6 клеток и 4 клетки. Применяя метод подсчета клеток, мы посчитали, что внутри прямоугольника находится 24 клетки. Таким образом, площадь прямоугольника равна 24 квадратным клеткам.
Пример 2: Метод сравнения площадей фигур
Возьмем две фигуры: квадрат со стороной 5 клеток и прямоугольник со сторонами 6 клеток и 4 клетки. Путем сравнения площадей фигур можно установить, что площадь квадрата равна 25 квадратным клеткам, а площадь прямоугольника – 24 квадратным клеткам. Таким образом, площадь квадрата больше площади прямоугольника.
Пример 3: Метод разбиения на дополнительные фигуры
Рассмотрим прямоугольник со сторонами 8 клеток и 3 клетки. С помощью метода разбиения на дополнительные фигуры мы выяснили, что этот прямоугольник можно разбить на два прямоугольника – один со сторонами 6 клеток и 3 клетки, и второй со сторонами 2 клетки и 3 клетки. Площади этих двух прямоугольников равны 18 и 6 квадратным клеткам соответственно. Суммируя их, получаем площадь исходного прямоугольника, которая равна 24 квадратным клеткам.
Таким образом, каждый из методов позволяет определить площадь прямоугольника на клетчатой бумаге, и выбор метода зависит от предпочтений и задачи, которую необходимо решить.






