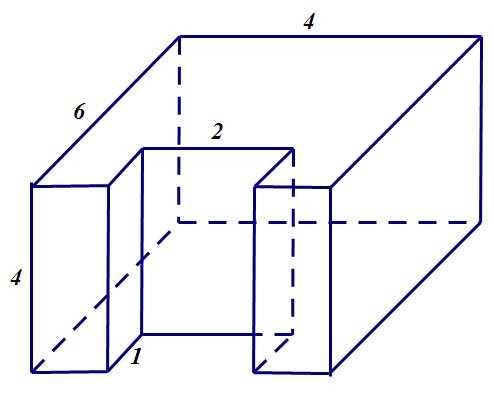
Когда мы сталкиваемся с задачей на нахождение площади поверхности многогранника на рисунке в задании ЕГЭ, это может показаться сложным и запутанным. Однако, с помощью подробного руководства у нас есть все шансы успешно разобраться с этой задачей. Важно понимать основные понятия и формулы, которые позволят нам вычислить площадь поверхности многогранника. Также стоит учесть, что для решения задачи нам потребуется анализировать и интерпретировать изображение на рисунке, чтобы правильно определить количество граней, их форму и размеры. Благодаря систематическому подходу и упорству мы сможем успешно найти площадь поверхности многогранника на рисунке в задании ЕГЭ.
Определение типа многогранника
Когда решаете задачу на определение площади поверхности многогранника на рисунке в задании ЕГЭ, первым делом нужно определить его тип. Ведь от типа многогранника зависит формула для подсчета площади. Как же быть, если вы не знаете, как определить тип многогранника?
Давайте разберемся. Самый простой способ – посмотреть на количество граней. Если у многогранника 4 грани, то это будет тетраэдр. Если 6 граней — это куб или гексаэдр. И так далее. Но что делать, если граней больше или несколько меньше? В таком случае, нужно обратить внимание на некоторые нюансы.
Если у многогранника всего одна грань, то это будет пирамида. Также можно заметить, что некоторые многогранники могут быть вытянутыми или сжатыми. Например, прямоугольный параллелепипед можно представить в виде куба, у которого одна сторона выдвинута или втянута.
Некоторые типы многогранников:
- Икосаэдр: многогранник с 20 гранями
- Додекаэдр: многогранник с 12 гранями
- Октаэдр: многогранник с 8 гранями
- Призма: две параллельные грани многоугольники
Если у вас все еще есть сомнения, то можно обратить внимание на особенности многогранника. Например, если у вас есть многогранник с 4 гранями, и он выглядит как куб, то, скорее всего, это и есть куб.
Важно помнить, что определение типа многогранника может быть сложным и требовать опыта. Но с практикой вы сможете быстро угадывать тип многогранника и успешно решать задачи на определение площади поверхности.
Надеюсь, эта информация поможет вам разобраться с определением типа многогранника и верно решить задачи на ЕГЭ. Удачи!
Шаг 1: Изучите рисунок
Прежде чем приступать к поиску площади поверхности многогранника на рисунке в задании ЕГЭ, важно внимательно изучить сам рисунок. Это первый и самый важный шаг, который поможет нам понять структуру многогранника и правильно определить его площадь.
Вопрос: Какие детали рисунка нам следует обратить внимание?
Мы обратим внимание на следующие аспекты:
- Форма многогранника
- Размеры сторон и углов
- Сетка или шаблон, по которому нарисован многогранник
- Линии, отмечающие углы и стороны многогранника
Изучение этих деталей поможет нам получить представление о структуре многогранника и понять, как вычислить его площадь.
Вопрос: Как мы можем использовать эту информацию при вычислении площади поверхности многогранника?
При изучении рисунка мы можем определить, какие факторы влияют на площадь многогранника. Например, если есть линии, отмечающие стороны многогранника, мы можем измерить их длину и использовать эту информацию при расчетах.
Также важно обратить внимание на форму и размеры многогранника. Некоторые многогранники имеют более сложную форму, например, пирамиды или призмы, и для их вычисления площади потребуется использовать специальные формулы.
Наконец, мы должны учитывать сетку или шаблон, по которому нарисован многогранник. Он может помочь нам разбить поверхность многогранника на более простые фигуры и вычислить их площади по отдельности. Это позволит нам получить итоговую площадь поверхности многогранника.
Итак, изучение рисунка является первым и самым важным шагом при поиске площади поверхности многогранника в задании ЕГЭ. Хорошее понимание его деталей поможет нам выбрать правильный подход при вычислении площади и достичь успешного решения задания.
Шаг 2: Определите количество граней

Чтобы определить количество граней, необходимо внимательно рассмотреть рисунок задания. Посмотрите на каждую сторону многогранника и подсчитайте их. Обратите внимание на то, что каждая грань должна быть четко различимой и отделенной от других поверхностей.
Если задание представляет собой трехмерный многогранник, то вам придется провести некоторые вычисления, чтобы определить количество граней. Обычно в таком случае используют формулу Эйлера, которая позволяет связать количество вершин, ребер и граней в многограннике.
Но не волнуйтесь, если вам необходимо использовать формулу Эйлера. В большинстве задач ЕГЭ количество граней обычно не является сложным для определения, и вы можете сосредоточиться на простом подсчете.
Запишите количество граней и продолжайте к следующему шагу: определение типа граней и их размеров.
Шаг 3: Определите тип многогранника
Теперь давайте рассмотрим, как определить тип многогранника на рисунке. Это важный шаг, так как тип многогранника влияет на дальнейшие вычисления. Есть несколько признаков, которые помогут вам определить тип многогранника:
- Количество граней: Если у многогранника 4 грани, то это четырёхугольная пирамида. Если у многогранника 6 граней, то это прямоугольный параллелепипед. Если у многогранника более 6 граней, то это может быть, например, правильная пирамида, правильный многоугольник или неравномерный многогранник.
- Стороны граней: Если все грани многогранника — правильные многоугольники (например, все грани являются равносторонними треугольниками или квадратами), то это правильный многогранник. Если же грани неравные, то это неравномерный многогранник.
- Углы: Если у многогранника все углы граней прямые, то это прямоугольный параллелепипед. Если же есть наклонные углы, то это может быть косоугольный параллелепипед или другой тип многогранника.
Итак, вы можете использовать эти признаки для определения типа многогранника. Но помните, что это не всегда просто, и иногда может потребоваться дополнительное изучение и анализ. Если у вас возникают сомнения, не стесняйтесь обратиться за помощью к учителю или преподавателю.
Вычисление площадей граней
1. Знание формулы: В первую очередь, вам нужно знать формулы для вычисления площадей различных граней. Например, для прямоугольника площадь вычисляется по формуле S = a * b, где a и b — длины его сторон. А для треугольника площадь можно вычислить по формуле S = (1/2) * a * h, где a — основание треугольника, а h — высота, опущенная на данное основание. Зная эти формулы, можно легко вычислять площади граней многогранников.
2. Разбиение многогранника на грани: Второй шаг — разбить многогранник на грани, для каждой из которых вы знаете формулу для вычисления площади. Например, для прямоугольного параллелепипеда вы можете разбить его на шесть прямоугольных граней, для которых площадь вычисляется по формуле S = a * b.
3. Измерение длин и высот: Третий шаг — измерить длины и высоты, необходимые для вычисления площадей граней. Например, для прямоугольного параллелепипеда вам понадобятся длины его сторон и высота.
4. Подсчет площадей граней: Четвертый шаг — подсчитать площади граней, используя измеренные длины и высоты в соответствующих формулах. Например, для прямоугольного параллелепипеда вы можете применить формулу S = a * b, где a и b — длины сторон данной грани.
5. Суммирование площадей: Последний шаг — сложить площади всех граней, чтобы получить общую площадь многогранника. Например, для прямоугольного параллелепипеда, вычислите площади всех шести граней и сложите их.
Таким образом, с помощью этих шагов, вы можете легко вычислить площади граней многогранников. Помните, что знание формул, разбиение многогранника на грани и измерение длин и высот являются ключевыми элементами в решении этой задачи. И не забывайте применять эти методы на практике, чтобы стать более уверенными в вычислении площадей граней многогранников.
Шаг 4: Разбейте многогранник на грани
Каждая грань имеет свою форму и размеры. Они могут быть треугольниками, прямоугольниками или любыми другими многоугольниками. Чтобы определить форму каждой грани, необходимо внимательно изучить рисунок и рассмотреть все углы и стороны многогранника.
Начните с первой грани и просто обведите ее контуром на бумаге. Учтите, что контур грани должен проходить по ребрам многогранника. Постепенно двигайтесь по многограннику, обводя каждую грань и подписывая ее номером для удобства.
Когда вы закончите разбивку многогранника на грани, у вас будет набор плоских полигонов, которые образуют поверхность многогранника. Теперь вы можете приступить к следующему шагу — нахождению площади каждой грани.
Шаг 5: Вычислите площадь каждой грани

Теперь, когда мы знаем все нужные данные, мы можем вычислить площадь каждой грани многогранника. Для этого мы используем различные геометрические формулы, в зависимости от типа грани и ее формы.
Вычисление площади каждой грани является важным шагом в нашем процессе решения заданий ЕГЭ, поскольку это помогает нам получить полное представление о поверхности многогранника. Кроме того, это позволяет нам проверить правильность наших предыдущих вычислений и убедиться, что мы правильно используем все данные, предоставленные в задании.
Как только мы вычислили площадь каждой грани, мы можем приступить к следующему шагу в нашем руководстве — вычислению общей площади поверхности многогранника. Это позволит нам окончательно ответить на поставленный в задании вопрос и завершить наше решение.






