Как найти площадь параллелограмма со сторонами 12 и 5: простой способ расчета

Как найти площадь параллелограмма со сторонами 12 и 5: простой способ расчета

У вас есть параллелограмм со сторонами 12 и 5, и вы хотите найти его площадь. Нет нужды беспокоиться! Расчет площади параллелограмма несложен, и я покажу вам простой способ сделать это.

Для начала, давайте вспомним, что площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону. В данном случае, мы знаем длины сторон – 12 и 5, и задача состоит в том, чтобы найти высоту.

Обратите внимание на то, что высота параллелограмма является перпендикулярным расстоянием от одной из его сторон до противоположной, а также, что сторона параллелограмма является основанием для вычисления высоты. Теперь, используя простые математические операции, мы сможем найти площадь этого параллелограмма. Время приступить к расчетам!

Знакомство с параллелограммом

Зачем нам нужно знать о параллелограммах? Они находят применение в разных областях нашей жизни. Например, если вы когда-нибудь сталкивались с областями, периметрами или объемами, то вам пригодятся знания о данной фигуре. Кроме того, параллелограммы – это простые и красивые геометрические формы, которые могут быть использованы для создания уникальных дизайнов, будь то логотипы, украшения или искусство.

Как определить, что перед вами именно параллелограмм? На первый взгляд, это может показаться сложным, но на самом деле все довольно просто. Обратите внимание на стороны фигуры – если они параллельны и одинаковой длины, то вы имеете дело именно с параллелограммом.

А что насчет площади параллелограмма? Очень просто! Для того чтобы найти площадь параллелограмма, умножьте длину одной из его сторон на высоту, опущенную на эту сторону. Например, если одна сторона равна 12, а высота – 5, то площадь параллелограмма будет равна 60.

Увидели, как просто?! Теперь вы знакомы с основами параллелограмма. Эта фигура имеет разнообразные применения и может быть источником вдохновения для дизайна и искусства. А расчет площади параллелограмма стал еще проще, благодаря формуле, которую мы только что поделили с вами. Так что не останавливайтесь на достигнутом, исследуйте мир геометрии и воплощайте свои творческие идеи с помощью параллелограммов!

Определение параллелограмма

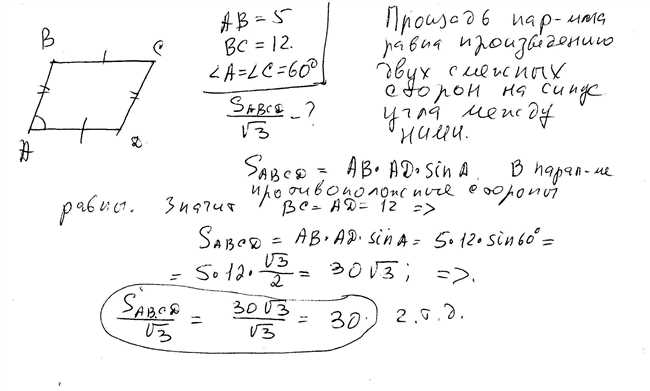
Когда мы говорим о сторонах параллелограмма, мы имеем в виду две пары: противоположные стороны. Например, если у нас есть параллелограмм со сторонами 12 и 5, это означает, что одна пара противоположных сторон равна 12, а другая пара равна 5.

Если нам нужно найти площадь такого параллелограмма, мы можем воспользоваться простой формулой: площадь равна произведению длины одной стороны на высоту, опущенную на эту сторону. Для параллелограмма это справедливо в силу свойства противоположных сторон. Таким образом, площадь параллелограмма со сторонами 12 и 5 может быть найдена как произведение 12 и высоты, которую мы будем находить.

Основные свойства параллелограмма

1. Противоположные стороны равны и параллельны.

• В параллелограмме противоположные стороны имеют одинаковую длину и параллельны друг другу.
• Это означает, что если у нас есть параллелограмм со сторонами AB и CD, то сторона AB будет равна и параллельна стороне CD, а сторона BC будет равна и параллельна стороне AD.

2. Противоположные углы равны.

• В параллелограмме противоположные углы имеют одинаковую меру.
• Это означает, что если у нас есть параллелограмм с углами A и C, то угол A будет равен углу C, а угол B будет равен углу D.

3. Смежные углы параллелограмма дополняют друг друга до 180°.

• Все смежные углы параллелограмма в сумме равны 180°.
• Это означает, что если у нас есть параллелограмм с углами A и B, то угол A и смежный с ним угол B в сумме составят 180°.

4. Диагонали параллелограмма делятся пополам.

• Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины.
• Диагонали параллелограмма делятся пополам, то есть они пересекаются в точке, которая является серединой каждой из них.

5. Площадь параллелограмма можно найти, умножив длину одной из сторон на высоту, опущенную на эту сторону.

• Высота параллелограмма — это отрезок, проведенный из одного угла параллелограмма к противоположной стороне.
• Площадь параллелограмма равна произведению длины одной из сторон на длину высоты, опущенной на эту сторону.

Зная эти основные свойства параллелограмма, мы можем легко рассчитать его площадь и выполнять другие операции с данной фигурой. Параллелограмм обладает множеством интересных свойств и может быть использован в различных сферах, например, для расчетов в геометрии или в архитектуре.

Формула для вычисления площади параллелограмма

Если вы хотите вычислить площадь параллелограмма, у которого известны длины его сторон, я могу поделиться с вами простой формулой, которая поможет вам справиться с этой задачей. Формула следующая:

Площадь параллелограмма = длина основания × высота

Ура! Правда, это проще, чем вы думали? Теперь у вас есть мощное оружие, чтобы рассчитать площадь любого параллелограмма. Давайте рассмотрим эту формулу более подробно.

Длина основания — это одна из сторон параллелограмма. Она может быть представлена как любая из его сторон. Важно запомнить, что для использования этой формулы вам нужно знать только одну из сторон параллелограмма.

Высота параллелограмма — это расстояние между основанием параллелограмма и противолежащей ему стороной. Оно перпендикулярно основанию и измеряется вдоль прямой линии, соединяющей основание с противолежащей стороной. Если вы не знаете высоту параллелограмма, не беда! Ее можно легко найти, используя другие известные параметры параллелограмма и геометрические свойства.

Например, если у вас есть параллелограмм со сторонами 12 и 5, и вы хотите найти его площадь, вы можете выбрать одну из сторон как основание, допустим, сторону 12. Затем вы можете найти высоту параллелограмма, используя геометрическую формулу или свойства параллелограмма. Зная длину основания и высоту, вы можете использовать формулу, чтобы вычислить площадь параллелограмма:

Площадь параллелограмма = 12 × высота

Вот и всё! Просто перемножьте длину основания на высоту параллелограмма в вашем случае и получите площадь. Это так просто!

Дополнительные советы:

• Убедитесь, что измерения основания и высоты выполняются в одних и тех же единицах измерения.
• Тщательно проверьте свои вычисления, чтобы избежать ошибок.
• Если у вас есть нерегулярный параллелограмм с неравными сторонами, вы можете использовать ту же формулу, но заменить длину основания и высоту соответствующими значениями.

Теперь, когда у вас есть эта полезная формула, вы можете смело решать задачи, связанные с вычислением площади параллелограмма. Знание этой формулы и некоторых дополнительных советов поможет вам стать настоящим гуру геометрии. Удачи в ваших математических приключениях!

Как найти площадь параллелограмма со сторонами 12 и 5

Если ты когда-либо интересовался, как найти площадь параллелограмма со сторонами 12 и 5, то сейчас я расскажу тебе простой способ расчета. Не волнуйся, это вовсе не сложно, и ты сможешь легко применить эту формулу для любого параллелограмма.

Для расчета площади параллелограмма, нужно знать длину одной из его сторон и высоту, опущенную на эту сторону. В нашем случае, у нас есть две стороны: 12 и 5. Давай начнем с определения высоты параллелограмма.

Высота параллелограмма — это расстояние между параллельными сторонами, которое опущено перпендикулярно от одной стороны до другой. Если ты не знаешь высоту, не беда! Мы можем ее найти, используя теорему Пифагора.

Пусть одна сторона параллелограмма равна 12, а высота параллелограмма равна h. Теперь мы можем использовать теорему Пифагора для определения h.

Теперь, когда у нас есть высота параллелограмма, мы можем легко найти его площадь, умножив длину одной из сторон на высоту. В нашем случае:

Площадь = 5(высота)

Площадь = 5h

Поэтому, чтобы найти площадь параллелограмма со сторонами 12 и 5, нужно умножить 5 на высоту параллелограмма, которую мы определили ранее с помощью теоремы Пифагора.

Теперь, когда ты знаешь этот простой способ, ты можешь применять его для расчета площади любого параллелограмма. Убедись, что ты правильно определил стороны и высоту, следуя нашим шагам, и получи точный результат. Удачи!

Примеры решения задач

Рассмотрим несколько примеров решения задач на нахождение площади параллелограмма с известными сторонами.

Пример 1:

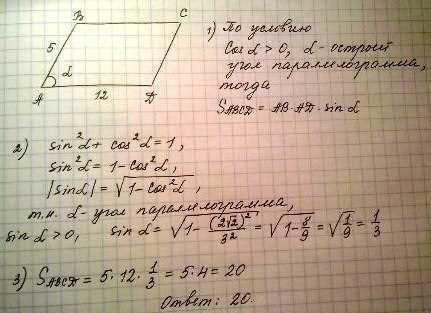
Дан параллелограмм со сторонами 12 и 5. Чтобы найти его площадь, нужно умножить длину одной стороны на высоту, опущенную на эту сторону.

Сначала рассчитаем высоту параллелограмма. Поскольку противоположные стороны параллелограмма параллельны и равны между собой, высота будет равна расстоянию между этими сторонами. В данном случае, это сторона длиной 5. Теперь у нас есть высота и одна сторона параллелограмма.

Подставляем значения в формулу для площади параллелограмма: площадь = сторона * высота, где сторона = 12 и высота = 5. Получаем: площадь = 12 * 5 = 60.

Таким образом, площадь параллелограмма со сторонами 12 и 5 равна 60.

Пример 2:

Предположим, что у нас есть параллелограмм со сторонами 8 и 6. Чтобы найти его площадь, также нужно умножить длину одной стороны на высоту, опущенную на эту сторону.

Рассчитаем высоту параллелограмма. Противоположные стороны параллелограмма параллельны и равны, поэтому высота будет равна расстоянию между этими сторонами. В данном случае это сторона длиной 6. Теперь у нас есть высота и одна сторона параллелограмма.

Подставляем значения в формулу для площади параллелограмма: площадь = сторона * высота, где сторона = 8 и высота = 6. Получаем: площадь = 8 * 6 = 48.

Таким образом, площадь параллелограмма со сторонами 8 и 6 равна 48.

Пример 3:

Пусть дан параллелограмм со сторонами 10 и 4. Чтобы найти его площадь, также нужно умножить длину одной стороны на высоту, опущенную на эту сторону.

Рассчитаем высоту параллелограмма. Противоположные стороны параллелограмма параллельны и равны, поэтому высота будет равна расстоянию между этими сторонами. В данном случае это сторона длиной 4. Теперь у нас есть высота и одна сторона параллелограмма.

Подставляем значения в формулу для площади параллелограмма: площадь = сторона * высота, где сторона = 10 и высота = 4. Получаем: площадь = 10 * 4 = 40.

Таким образом, площадь параллелограмма со сторонами 10 и 4 равна 40.

• Пример 1: площадь параллелограмма со сторонами 12 и 5 равна 60.
• Пример 2: площадь параллелограмма со сторонами 8 и 6 равна 48.
• Пример 3: площадь параллелограмма со сторонами 10 и 4 равна 40.