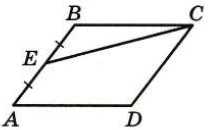
Как найти площадь параллелограмма ABCD с известной серединой стороны AD равной 96? Когда у нас есть фигура, состоящая из параллельных сторон и противоположных углов, мы можем использовать различные методы для вычисления ее площади. В данном случае, зная середину стороны AD, мы можем применить формулу для вычисления площади параллелограмма, которая основана на длине основания и высоте. С помощью данной формулы, мы можем определить площадь параллелограмма ABCD, чтобы получить точный результат. Таким образом, нахождение площади параллелограмма с известной серединой стороны AD равной 96 не представляет больших сложностей при использовании соответствующих вычислительных методов.
Определение параллелограмма
Один из самых важных аспектов, который отличает параллелограмм от других четырехугольников, — это то, что его противоположные стороны параллельны. Это означает, что если на одной стороне параллелограмма провести прямую линию, то она будет параллельна и равна противоположной стороне.
У параллелограмма также есть другие характеристики, которые его отличают. Например, его противоположные углы равны между собой. Это значит, что если измерить углы, образованные противоположными сторонами параллелограмма, то они будут равны. Также все углы параллелограмма являются тупыми или острыми.
Кроме того, параллелограмм имеет две перпендикулярные диагонали, которые делят его на четыре равных треугольника. Эти диагонали пересекаются в точке, называемой центром параллелограмма, которая также является серединой каждой из диагоналей.
Вот некоторые ключевые характеристики параллелограмма:
- Противоположные стороны параллельны и равны.
- Противоположные углы равны.
- Все углы параллелограмма являются тупыми или острыми.
- У параллелограмма есть две перпендикулярные диагонали, делящие его на четыре равных треугольника.
- У параллелограмма есть центр, который является пересечением диагоналей.
Теперь, когда мы знаем определение параллелограмма, давайте рассмотрим, как мы можем найти площадь параллелограмма ABCD с известной серединой стороны AD, равной 96.
Середина стороны AD
Середина стороны AD параллелограмма ABCD играет важную роль при вычислении его площади. Чтобы понять, почему это так, давайте разберемся, что такое середина стороны.
Середина стороны AD — это точка, которая расположена на равном удалении от точки A и точки D, образуя прямую линию. Она делит сторону AD на две равные части.
Какая связь между серединой стороны и площадью параллелограмма? Давайте рассмотрим следующую ситуацию: если мы проведем линию, соединяющую середину стороны AD с точкой B, то получим две равных треугольника — ABD и BCD.

Площадь треугольника равна половине произведения длины основания на высоту. Таким образом, если мы знаем длину стороны AD и высоту параллелограмма, то можем вычислить площадь одного из треугольников. А так как площадь параллелограмма равна сумме площадей двух треугольников, мы можем получить итоговую площадь параллелограмма.
В нашем случае, когда известна середина стороны AD равная 96, мы можем использовать ее для вычисления высоты параллелограмма. Для этого мы удваиваем значение середины, то есть 96 * 2 = 192, и получаем значение высоты.
- Длина основания AD: неизвестно (обозначим ее х)
- Середина стороны AD: 96
- Высота параллелограмма: 192
Теперь мы можем использовать известные значения для вычисления площади параллелограмма по формуле: S = х * 192.
Важно отметить, что для полной раскраски темы «Как найти площадь параллелограмма ABCD с известной серединой стороны AD равной 96», нужно учитывать и другие стороны параллелограмма и углы между ними. Однако, знание середины стороны AD позволяет сократить вычисления и найти площадь проще и быстрее.
Нахождение длины стороны BC:
Чтобы найти длину стороны BC параллелограмма ABCD, мы можем использовать свойство параллелограмма, согласно которому стороны, соединяющие одинаковые вершины, имеют равные длины.
Зная, что середина стороны AD равна 96, мы можем предположить, что это является половиной длины стороны AD.
Таким образом, длина стороны AD будет равна 96 * 2 = 192.
Теперь мы можем использовать это значение, чтобы найти длину стороны BC.
Сторона BC является противоположной стороной AD, поэтому они равны по длине. Значит, длина стороны BC также будет 192.
Таким образом, длина стороны BC параллелограмма ABCD составляет 192.
Возможно, это может показаться немного сложным, но если мы применим свойства параллелограмма и внимательно проанализируем данные, мы сможем найти нужную нам информацию.
Итак, длина стороны BC равна 192.
Расчет площади параллелограмма
Дано: параллелограмм ABCD, середина стороны AD равна 96.
Шаг 1: Найдем длину стороны AD. Известно, что середина стороны AD равна 96. Пусть точка M — середина стороны AD. По теореме о средней линии треугольника, длина средней линии равна половине суммы длин оснований. Тогда длина стороны AD равна удвоенной длине средней линии AM: AD = 2 * AM. Таким образом, длина стороны AD равна 2 * 96 = 192.
Шаг 2: Найдем длину стороны BC. Параллелограмм ABCD имеет противоположные стороны, равные по длине. Значит, сторона BC также равна 192.
Шаг 3: Найдем площадь параллелограмма ABCD. Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону. В данном случае, длина стороны одна из его сторон равна 192, а высоту опускаем на эту сторону мы не знаем. Поэтому невозможно найти точное значение площади параллелограмма ABCD без дополнительной информации о высоте.






