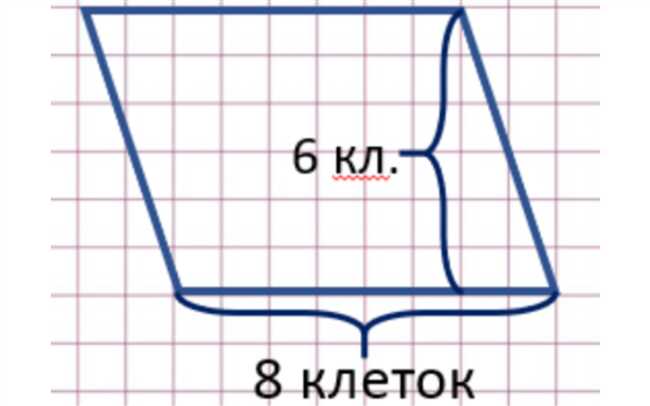
Вы когда-нибудь задумывались, как найти площадь параллелограмма? Эта задача может показаться сложной на первый взгляд, но на самом деле существуют простые формулы для ее решения.
Один из способов найти площадь параллелограмма ABCD — умножить длину его основания на высоту, опущенную на это основание. Другими словами, S = a * h, где S — площадь, a — длина основания, а h — высота параллелограмма.
Однако, иногда высоту неизвестно. В этом случае можно использовать другую формулу: S = ab * sin(θ), где а и b — длины сторон параллелограмма, а θ — угол между этими сторонами.
Давайте рассмотрим несколько примеров расчета площади параллелограмма ABCD, чтобы лучше разобраться в этой теме.
Определение параллелограмма
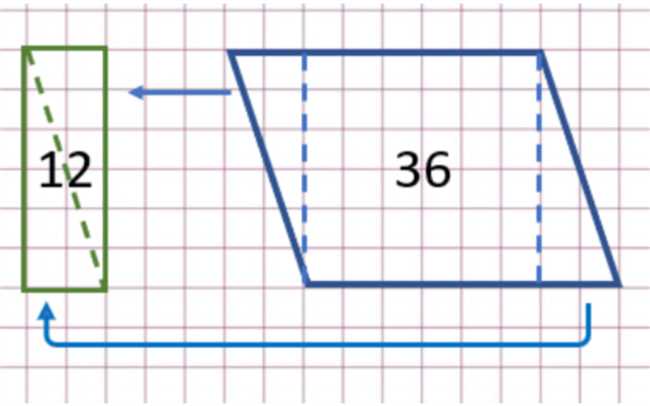
Основное определение параллелограмма заключается в том, что это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Это значит, что если взять две противоположные стороны параллелограмма и провести прямую линию параллельно этим сторонам, она будет пересекать остальные две стороны в одной и той же точке.
Структура параллелограмма имеет свои особенности. Его противоположные стороны равны по длине, и их называют основаниями параллелограмма. А противоположные стороны, соединяющие соответствующие вершины, формируют параллельные отрезки, которые называются боковыми сторонами параллелограмма.
Одно из ключевых свойств параллелограмма – равенство противоположных углов. Это означает, что между каждой парой противоположных углов параллелограмма существует равенство. Например, если один угол параллелограмма равен 60°, то и его противоположный угол также будет равен 60°.
Примеры:
- Прямоугольник – это частный случай параллелограмма, у которого все углы равны 90°.
- Квадрат также является частным случаем параллелограмма, у которого все стороны параллельны и равны по длине, и все углы равны 90°.
Теперь, когда вы понимаете, что такое параллелограмм и как его определить, вы можете использовать эту информацию в геометрии, чтобы решать задачи и находить площадь параллелограмма, его периметр и другие параметры. Откройте для себя мир геометрии и наслаждайтесь изучением различных фигур!
Формула для расчета площади параллелограмма
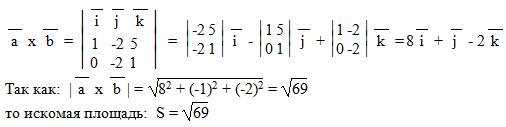
Формула для расчета площади параллелограмма:
Площадь параллелограмма равна произведению длины одной из его сторон на высоту, проведенную к этой стороне.
| Формула | Обозначения |
|---|---|
| S = a * h |
S — площадь параллелограмма a — длина одной из сторон параллелограмма h — высота, проведенная к этой стороне |
Теперь разберемся, как использовать данную формулу на практике. Допустим, мы имеем параллелограмм ABCD.
Пример 1:
Известно, что одна из сторон параллелограмма равна 5 см, а высота, проведенная к этой стороне, равна 3 см. Чтобы найти площадь параллелограмма, умножим длину стороны на высоту:
S = 5 см * 3 см = 15 см²
Ответ: площадь параллелограмма равна 15 см².
Пример 2:
Предположим, что длина одной из сторон параллелограмма равна 8 м, а высота, проведенная к этой стороне, равна 2 м. Применяем формулу:
S = 8 м * 2 м = 16 м²
Ответ: площадь параллелограмма равна 16 м².
Теперь, когда у вас есть формула для расчета площади параллелограмма и несколько примеров, вы можете с легкостью решать подобные задачи. Не забывайте, что длина стороны и высота должны быть в одном и том же измерении (например, в сантиметрах или в метрах).
Примеры расчета площади параллелограмма
В данной статье мы рассмотрели несколько примеров расчета площади параллелограмма. Зная длину базы и высоту, мы можем легко найти площадь параллелограмма, используя формулу S = a * h. Также, если известны длины сторон и угол между ними, мы можем воспользоваться формулой S = a * b * sin(α).
Пример 1: Для параллелограмма ABCD со сторонами a = 6 см и b = 8 см, а углом α = 60 градусов, площадь вычисляется следующим образом. S = 6 см * 8 см * sin(60°) = 24√3 см².
Пример 2: Параллелограмм EFGH имеет длину базы равную 10 м и высоту 4 м. Чтобы найти площадь, мы используем формулу S = a * h. S = 10 м * 4 м = 40 м².
- — Площадь параллелограмма можно найти, зная длину базы и высоту, либо длины сторон и угол между ними;
- — Формулы для расчета площади параллелограмма: S = a * h и S = a * b * sin(α);
- — Ответы представленные в данной статье: S = 24√3 см² (пример 1) и S = 40 м² (пример 2).
Знание этих формул и примеров расчета позволит вам легко вычислять площадь параллелограмма в различных задачах и ситуациях.






