
В 3 классе, дети начинают знакомство с геометрией и учатся находить периметр и площадь многоугольника. Периметр многоугольника — это сумма всех его сторон, а площадь — это количество площадных единиц внутри фигуры.
Поиск периметра и площади может быть легко освоен с помощью простых шагов и примеров. Дети могут использовать формулы или строить многоугольники на клетчатой бумаге для определения периметра и площади. Учитель может помочь им понять принципы и правила для этих вычислений.
Находя периметр и площадь многоугольников, дети развивают логическое мышление, абстрактное мышление и математические навыки. Эти навыки очень важны для дальнейшего изучения геометрии и математики в школе.
Определение многоугольника
Многоугольник может быть выпуклым или невыпуклым. Если все углы многоугольника менее 180 градусов, то он будет выпуклым. Невыпуклый многоугольник имеет хотя бы один угол, больший 180 градусов.
Имена многоугольников определяются их количеством сторон. Например, треугольник имеет три стороны, квадрат — четыре стороны, пятиугольник — пять сторон и так далее.
Каждая сторона многоугольника соединяется двумя соседними сторонами, а вершина — точка пересечения двух сторон. Чтобы образовать многоугольник, можно соединить любые вершины отрезками, но важно, чтобы не было самопересечений и все стороны многоугольника не пересекались или касались внутри фигуры.
Многоугольники встречаются везде в нашей жизни. Например, двери, окна, столы и другие предметы могут иметь форму треугольника, прямоугольника или квадрата. Многоугольники также используются в архитектуре и строительстве для создания различных форм и структур.
Понимание определения многоугольника поможет нам легче разбираться с его характеристиками, такими как площадь и периметр. С помощью этих понятий мы сможем изучить и исследовать различные многоугольники и использовать их в нашей повседневной жизни.
Как найти периметр многоугольника
Стоит отметить, что каждая форма многоугольника имеет свои особенности, что делает процесс нахождения периметра немного разным для разных фигур. В этом объяснении я расскажу общий подход, который будет работать для большинства многоугольников.
Вот шаги, которые помогут тебе найти периметр многоугольника:
- Запиши длины всех сторон: прежде всего, нужно определить все стороны многоугольника и замерить их длины с помощью линейки или другого измерительного инструмента. Не забудь записать все измерения для удобства.
- Сложи длины всех сторон: как только у тебя есть все измерения, сложи их вместе. Это даст тебе общую длину всех сторон многоугольника.
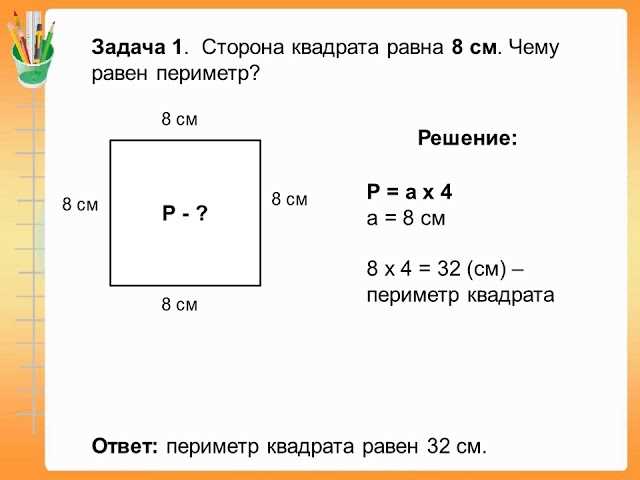
Пример: давай рассмотрим квадрат. Квадрат имеет четыре равные стороны, поэтому нам просто нужно замерить одну сторону и умножить ее на 4, чтобы получить периметр.
| Сторона | Длина |
|---|---|
| AB | 5 см |
| BC | 5 см |
| CD | 5 см |
| DA | 5 см |
Периметр квадрата = 5 см + 5 см + 5 см + 5 см = 20 см.
А теперь представь, что у тебя есть другая фигура, например, треугольник или пятиугольник. Что делать в таком случае? Просто замерь все стороны и сложи их вместе, аналогично тому, как мы делали с квадратом.
Теперь, у тебя есть простой метод для нахождения периметра многоугольника! Только не забывай замерять и записывать все измерения аккуратно, чтобы твои расчеты были точными.
Надеюсь, это помогло тебе понять, как найти периметр многоугольника. Удачи в изучении геометрии!
Как найти площадь многоугольника?

Для начала, давай разберемся, что такое многоугольник. Многоугольник — это фигура, состоящая из трех или более сторон, которые соединены вершинами. Примерами многоугольников могут быть треугольник, четырехугольник (квадрат, прямоугольник) или пятиугольник (пятиконечная звезда).
Самый простой способ найти площадь многоугольника — это разделить его на прямоугольники или треугольники, для которых мы уже знаем как найти площадь. Затем сложим площади всех этих фигур и получим общую площадь многоугольника.
Но что делать, если у нас нет прямоугольников или треугольников, на которые можно разбить многоугольник? Тогда нам поможет формула для нахождения площади многоугольника — формула Гаусса. Формула Гаусса гласит, что площадь многоугольника можно найти, если мы знаем координаты его вершин.
Давай посмотрим на примере. Представь, что у нас есть треугольник с координатами вершин (x1, y1), (x2, y2) и (x3, y3). Чтобы найти площадь этого треугольника, мы используем следующую формулу:
- Площадь = 0.5 * |(x1 *(y2 — y3) + x2 * (y3 — y1) + x3 * (y1 — y2))|
Эта формула вычисляет площадь треугольника, исходя из координат его вершин. Таким же образом мы можем вычислить и площадь любого другого многоугольника, используя соответствующие формулы для указанного количества вершин.
Теперь ты знаешь, как найти площадь многоугольника. Это очень полезное знание, которое ты можешь применить не только в учебе, но и в повседневной жизни. Например, при рассчете площади комнаты или огорода.
Держи в голове эту простую и эффективную формулу, и ты всегда сможешь легко вычислить площадь любого многоугольника. Удачи!
Заключение
В данной статье мы рассмотрели примеры вычисления периметра и площади многоугольника. Во время изучения геометрии в 3 классе, учащиеся начинают знакомиться с основными понятиями и методами вычисления площади и периметра фигур.
Мы изучили базовые правила определения периметра и площади многоугольника. Для вычисления периметра необходимо просуммировать длины всех сторон фигуры. А для вычисления площади можно использовать формулу, основанную на подсчете количества квадратных единиц внутри фигуры.
Приведенные примеры позволят учащимся легче понять и применить эти правила на практике. Они могут использовать данные примеры для самостоятельной работы и тренировки навыков вычисления площади и периметра многоугольников.
Понимание основных концепций позволяет детям развивать логическое мышление и увереннее работать с геометрическими фигурами. Вычисление площади и периметра многоугольников — это не только важные математические навыки, но и умение применять полученные знания в повседневной жизни.
Важно помочь детям увидеть применение этих знаний в реальном мире, например, при измерении площади комнаты или периметра забора на даче. Таким образом, изучение периметра и площади многоугольника облегчает учащимся понимание основ математики и способствует их развитию.






