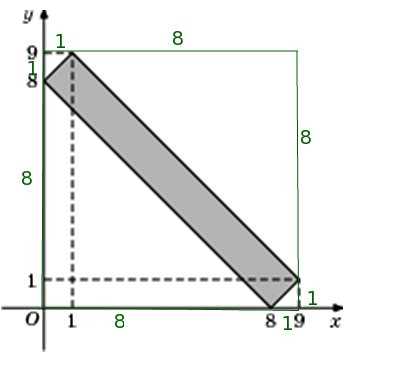
Подсчет площади фигуры по координатам ее вершин – важный элемент геометрии. Существует несколько простых способов для определения площади таких фигур, как треугольник, прямоугольник и многоугольник.
Первый способ – использование формулы для нахождения площади треугольника: половина произведения длины основания на высоту.
Второй способ подходит для прямоугольника, его площадь определяется как произведение длины одной стороны на длину другой.
Третий способ применим для многоугольника и основывается на разбиении его на треугольники и суммировании их площадей. Каждый треугольник может быть вычислен отдельно, затем полученные значения суммируются, чтобы найти общую площадь.
С использованием этих трех способов можно легко определить площадь фигуры по координатам вершин.
Площадь треугольника
Первый способ, который мы рассмотрим — это формула Герона. Она основана на полупериметре треугольника и длинах его сторон. Для использования этой формулы необходимо знать все три стороны треугольника. Полупериметр треугольника можно найти, сложив длины всех его сторон и разделив полученную сумму на 2. Затем, используя найденные значения, мы сможем вычислить площадь треугольника по формуле Герона.
Второй способ основан на применении векторных операций. Векторы представляют собой математические объекты, которые имеют направление и длину. В данном случае мы будем использовать векторное произведение для вычисления площади треугольника. Для этого необходимо найти координаты векторов, соединяющих вершины треугольника, а затем применить формулу для векторного произведения. Результат этой операции будет являться площадью треугольника.
Третий способ основан на использовании матриц. Матрицы — это таблицы чисел, упорядоченных в определенном порядке. В данном случае мы будем использовать матрицу координат вершин треугольника. Для вычисления площади треугольника по его координатам необходимо взять половину определителя матрицы координат и взять его абсолютное значение. Получившееся число будет являться площадью треугольника.
Теперь, когда мы рассмотрели основные способы вычисления площади треугольника по его координатам, давайте решим небольшую задачу. У нас есть треугольник со следующими координатами вершин: A(1,1), B(4,3) и C(2,6). Мы можем воспользоваться любым из рассмотренных способов.
Например, воспользуемся формулой Герона. Найдем длины сторон треугольника: AB, BC и AC, а затем найдем полупериметр треугольника. Подставив полученные значения в формулу Герона, мы получим площадь треугольника.
По формуле Герона:
AB = √((4-1)^2 + (3-1)^2) = √(3^2 + 2^2) = √(9+4) = √13
BC = √((2-4)^2 + (6-3)^2) = √((-2)^2 + 3^2) = √(4+9) = √13
AC = √((2-1)^2 + (6-1)^2) = √(1^2 + 5^2) = √(1+25) = √26
Полупериметр треугольника: p = (AB + BC + AC) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 = (√13 + √13 + √26) / 2 ≈ 6.52
Площадь треугольника: S = √(p * (p — AB) * (p — BC) * (p — AC)) = √(6.52 * (6.52 — √13) * (6.52 — √13) * (6.52 — √26)) ≈ √(6.52 * (6.52 — 3.61) * (6.52 — 3.61) * (6.52 — 5.1)) ≈ √(6.52 * 2.91 * 2.91 * 1.42 ) ≈ √63.09 ≈ 7.95
Таким образом, площадь треугольника со сторонами AB, BC и AC, заданными координатами вершин A(1,1), B(4,3) и C(2,6), составляет примерно 7.95 квадратных единиц.
Как видите, вычисление площади треугольника по его координатам несложно, если знать базовые математические концепции и использовать подходящие формулы. Используя один из представленных способов, вы всегда сможете вычислить площадь треугольника с высокой точностью. Это навык, который пригодится вам не только в школе, но и в различных сферах жизни, где математика играет важную роль.
Площадь прямоугольника
Для того чтобы найти площадь прямоугольника, нужно знать длину его сторон. Если у нас есть две стороны прямоугольника, допустим, сторона А и сторона В, мы можем просто умножить их длины, чтобы получить площадь.
Формула для нахождения площади прямоугольника выглядит следующим образом:
Площадь прямоугольника = длина стороны А * длина стороны В
Давайте рассмотрим пример. Представьте себе, что у нас есть прямоугольник со сторонами, длина которых равна 5 единицам, а ширина равна 3 единицам. Чтобы найти площадь этого прямоугольника, мы просто перемножим эти два числа: 5 * 3 = 15. Таким образом, площадь прямоугольника равна 15 единицам.
Прямоугольники широко используются в повседневной жизни. Например, они часто встречаются в строительстве, архитектуре и дизайне интерьеров. Площадь прямоугольника может быть полезной для расчета количества материала, необходимого для покрытия поверхности, или для оценки пространства, занимаемого прямоугольным объектом. Зная формулу и способы вычисления площади прямоугольника, мы можем с легкостью решать такие задачи и использовать это знание в повседневной жизни.
Запомни формулу и попробуй самостоятельно найти площадь прямоугольников с разными сторонами. Учись видеть применение геометрии вокруг себя и не бойся использовать эти знания в практических ситуациях!
Площадь многоугольника
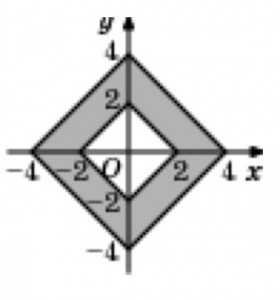
Существует несколько способов вычисления площади многоугольника, включая методы разделения его на треугольники, использование формулы Гаусса и метод геометрических вычислений. Рассмотрим каждый из них подробнее.
1. Метод разбиения на треугольники
Этот метод основан на том, что любой многоугольник можно разбить на несколько треугольников и затем сложить их площади. Для этого проводят диагонали – отрезки, соединяющие любые две несоседние вершины. Полученный многоугольник разбивается на треугольники, площади которых уже можно легко вычислить с помощью формулы для площади треугольника (половина произведения длины основания на высоту).
2. Формула Гаусса
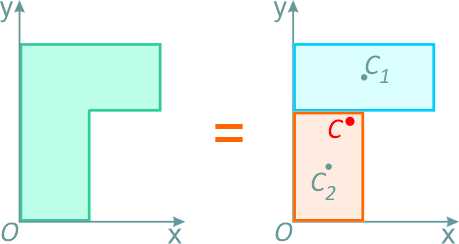
Формула Гаусса позволяет быстро вычислять площадь многоугольника, если известны координаты его вершин. Для применения этой формулы необходимо знать порядок обхода вершин многоугольника, который должен быть последовательным и не пересекающим себя. Формула Гаусса гласит: площадь многоугольника равна половине суммы произведений абсцисс вершин на разность ординат соседних вершин.
Понять это на практике легче, поэтому предлагаю попробовать применить формулу Гаусса на примере многоугольника, заданного координатами его вершин:
| Вершина | Координаты |
|---|---|
| A | (2, 2) |
| B | (5, 6) |
| C | (8, 3) |
| D | (5, 2) |
Применим формулу Гаусса и получим:
- AB × (By — Ay) = 3 × (6 — 2) = 12
- BC × (Cy — By) = 3 × (3 — 6) = -9
- CD × (Dy — Cy) = -3 × (2 — 3) = 3
- DA × (Ay — Dy) = -3 × (2 — 2) = 0
Суммируем полученные значения и находим площадь многоугольника по формуле Гаусса: 12 + (-9) + 3 + 0 = 6.
3. Метод геометрических вычислений
Этот метод подходит для нахождения площади простых многоугольников или многоугольников, которые можно разбить на простые фигуры, такие как прямоугольники, треугольники и трапеции. Для этого необходимо разбить многоугольник на такие фигуры и вычислить их площади отдельно, а затем сложить их в общую площадь многоугольника.
Рассмотрим пример нахождения площади прямоугольного многоугольника:
Допустим, у нас есть прямоугольный многоугольник с высотой h и основанием a. Его площадь равна произведению длины основания на высоту: S = a × h.
А теперь представьте, что а наш прямоугольный многоугольник состоит из нескольких таких многоугольников. Мы можем разбить его на n таких многоугольников и затем найти площадь каждого из них отдельно, а затем сложить их в общую площадь прямоугольного многоугольника.
Таким образом, площадь многоугольника – это не только простая математическая задача, но и возможность взглянуть на мир геометрии с новой стороны. Независимо от того, какой способ подсчета площади многоугольника вы выберете, запомните, что главное – это точность и систематичность.
Применение формулы площади
Когда мы имеем дело с геометрическими фигурами и нужно найти их площадь, мы часто обращаемся к формулам. Формулы площади помогают нам вычислить площадь различных фигур, используя данные, которые у нас есть, обычно заданные в виде координат вершин.
Применение формулы площади может быть полезно во многих ситуациях. Например, если вы хотите уложить новый ковер в своей гостиной, вы можете использовать формулу площади, чтобы узнать, сколько ковра вам нужно купить. Если вы строите новый забор вокруг своего заднего двора, формула площади поможет вам определить количество материала, необходимого для постройки забора.
Формулы площади также могут быть полезны в научных и инженерных расчетах. Например, если вы работаете над проектом строительства моста, вам может потребоваться вычислить площадь покрытия дороги или площадь покрытия бетона для фундамента моста. Формула площади поможет вам получить точные данные, которые нужны для выполнения проекта.
- Формулы площади — это математические уравнения, которые позволяют вычислить площадь различных фигур.
- Применение формулы площади облегчает вычисления и помогает получить точные результаты для различных задач.
- Формулы площади могут быть использованы для решения различных практических задач, таких как покупка материалов или выполнение строительных проектов.
Важные замечания
При использовании любого из представленных способов для нахождения площади фигуры по координатам вершин, следует обратить внимание на несколько важных замечаний:
- Вершины должны быть упорядочены: Для правильного расчета площади, вершины фигуры должны быть упорядочены по часовой стрелке или против часовой стрелки. Это поможет избежать ошибок в расчетах и получить правильный результат.
- Точность координат: Координаты вершин должны быть указаны с высокой точностью, особенно если фигура имеет сложную форму. Округление или неправильное указание координат может привести к неточным результатам расчета площади.
- Учет пересечений: Если фигура имеет самопересечения, то расчет площади должен быть выполнен с учетом всех сегментов фигуры. В этом случае можно разбить фигуру на несколько непересекающихся частей и найти площадь каждой из них, а затем сложить результаты.
Учитывая эти важные замечания, вы сможете точно и правильно находить площадь фигур по координатам и использовать этот навык для решения различных геометрических задач.






