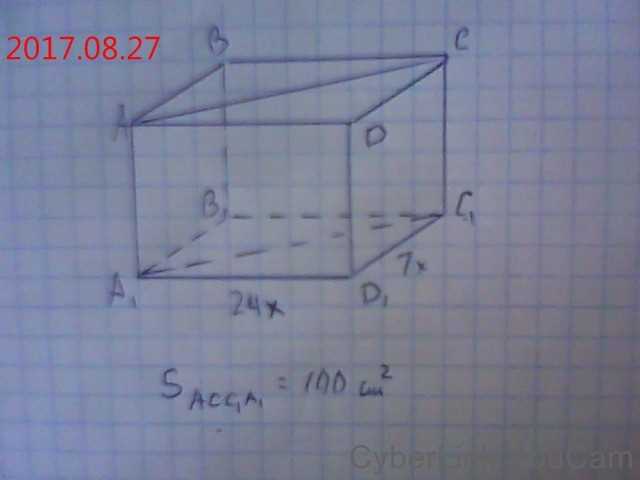
Когда мы рассматриваем геометрические фигуры, важно понимать, как найти их характеристики, такие как площадь. Если мы говорим о параллелепипеде — трехмерной фигуре с шестью прямоугольными гранями, то нас интересует вопрос: «Как найти площадь его диагонального сечения?».
Для решения этой задачи мы можем использовать специальную формулу, которая позволяет нам вычислить площадь диагонального сечения параллелепипеда. Но важно помнить, что сперва нужно знать длину и ширину грани параллелепипеда, из которой мы строим сечение. Только с такой информацией мы можем приступить к расчетам и найти площадь диагонального сечения.
Определение параллелепипеда
Параллелепипеды встречаются в повседневной жизни очень часто. Например, упаковка кирпича, коробка для карандашей, книг или даже дома — все они могут быть представлены в виде параллелепипеда.
Для лучшего представления о том, что такое параллелепипед, давайте рассмотрим несколько примеров. Представьте, что у вас есть коробка, в которой вы храните свои книги. Коробка имеет три измерения: длину, ширину и высоту. Если все три измерения равны (например, 20 см), это будет куб (специальный случай параллелепипеда). Однако, если хотя бы одно измерение отличается от других, это уже будет обычный параллелепипед. Например, если длина составляет 20 см, ширина — 15 см и высота — 10 см, это будет параллелепипед.
Теперь, когда вы знаете, что такое параллелепипед, вы можете приступить к решению задач, связанных с его свойствами, например, вычислением площади диагонального сечения. Удачи в ваших геометрических приключениях!
Формула для расчета площади диагонального сечения
Перед нами стоит задача найти площадь диагонального сечения параллелепипеда. Это может быть полезно в различных ситуациях, например, при проектировании зданий или при расчете объема материалов, необходимых для заполнения пространства. Но как нам найти эту площадь?
Для расчета площади диагонального сечения нам понадобится знание формулы для площади параллелепипеда. Эта формула гласит, что площадь параллелепипеда равна произведению длины одной из его сторон на площадь основания. То есть:
Площадь параллелепипеда = длина x ширина x высота
Теперь, чтобы найти площадь диагонального сечения параллелепипеда, нам необходимо знать длину диагонали этого сечения. Диагональ диагонального сечения — это прямая линия, соединяющая противоположные углы сечения. Зная длину этой диагонали, мы можем применить формулу для нахождения площади.
Формула для расчета площади диагонального сечения имеет вид:
Площадь диагонального сечения = (длина диагонали x ширина диагонали) / 2
Используя эту формулу, мы можем легко находить площадь диагонального сечения параллелепипеда, зная длину и ширину диагонали. Например, представим себе параллелепипед со сторонами 4, 6 и 8 сантиметров. Чтобы найти площадь диагонального сечения, нам нужно знать длину и ширину диагонали. Предположим, что длина диагонали составляет 10 сантиметров, а ширина диагонали — 6 сантиметров. Применяя формулу, получаем:
Площадь диагонального сечения = (10 см x 6 см) / 2 = 30 см²
Таким образом, площадь диагонального сечения параллелепипеда равна 30 квадратным сантиметрам.
Итак, теперь у вас есть формула для расчета площади диагонального сечения параллелепипеда. Она довольно проста в использовании и позволяет решать множество задач. Попробуйте применить эту формулу в своих расчетах и посмотрите, как она поможет вам получить точные результаты.
Пример расчета площади диагонального сечения

Давайте рассмотрим пример расчета площади диагонального сечения параллелепипеда. Представим, что у нас есть параллелепипед с шириной 6 м, высотой 4 м и длиной 8 м. Мы хотим найти площадь диагонального сечения параллелепипеда.
Чтобы найти площадь диагонального сечения, нам понадобится использовать формулу: S = a * b * sin(α), где a и b — стороны прямоугольника, а α — угол между ними.
В нашем примере у нас есть параллелепипед, и мы хотим найти площадь диагонального сечения, поэтому мы можем считать, что a и b — стороны прямоугольника, а α — угол между ними, равен 90 градусам.
Теперь подставим известные значения в формулу: S = 6 * 4 * sin(90). Угол sin(90) равен 1, поэтому просто оставим его без изменений: S = 6 * 4 * 1 = 24 м².
Таким образом, площадь диагонального сечения параллелепипеда равна 24 м².
Не забывайте, что этот пример является всего лишь одним из множества возможных расчетов площади диагонального сечения. В каждом конкретном случае значения сторон и углов могут отличаться, поэтому всегда проверяйте формулу и подставляйте правильные значения.
Зависимость площади диагонального сечения от параметров параллелепипеда
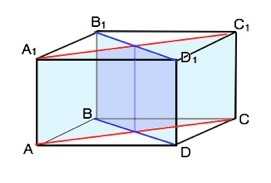
Площадь диагонального сечения параллелепипеда зависит от его параметров, таких как длина, ширина и высота. Для расчета этой площади используется специальная формула, которая позволяет получить точный результат. Давайте разберемся, как эти параметры влияют на площадь диагонального сечения параллелепипеда.
Когда мы говорим о диагональном сечении параллелепипеда, мы имеем в виду плоскость, которая проходит через его диагональ. Найдя размеры этого сечения, мы сможем рассчитать его площадь.
Длина и ширина диагонального сечения
Длина и ширина диагонального сечения параллелепипеда зависят от длины и ширины самого параллелепипеда, а также от угла, под которым происходит сечение. Если мы представим себе параллелепипед в виде овощного ящика, длина его диагонального сечения будет равна длине самого ящика, а ширина — ширине ящика. При изменении длины и ширины параллелепипеда, соответственно, будут изменяться и размеры диагонального сечения.
Высота диагонального сечения
Высота диагонального сечения параллелепипеда определяется его высотой и углом, под которым происходит сечение. Если параллелепипед представить в виде книжного ящика, высота диагонального сечения будет зависеть от высоты самого ящика и угла сечения. При изменении высоты параллелепипеда или угла сечения, будет изменяться и высота диагонального сечения.
Таким образом, площадь диагонального сечения параллелепипеда зависит от его параметров — длины, ширины и высоты, а также от угла, под которым происходит сечение. При изменении этих параметров площадь диагонального сечения также будет меняться.
- Площадь диагонального сечения параллелепипеда может быть рассчитана с использованием формулы: S = h * l * sin(α), где h — высота параллелепипеда, l — длина диагонали параллелепипеда, α — угол между диагональю и высотой параллелепипеда.
- С помощью данной формулы можно определить площадь диагонального сечения в различных случаях, например, при известных значениях высоты, длины диагонали и угла.
- Расчет площади диагонального сечения может быть полезен при проектировании и строительстве, а также в других сферах, связанных с геометрией и расчетами объемов и площадей.
В целом, знание формулы и умение рассчитывать площадь диагонального сечения параллелепипеда является важным навыком для выполнения различных расчетов и задач, связанных с геометрией и строительством.






