Когда мы сталкиваемся с геометрическими фигурами, одним из первых вопросов, который возникает, является вычисление их площади. Четырёхугольники — это фигуры, у которых четыре стороны и четыре угла. Как найти площадь четырёхугольника? Существует несколько методов для этого.
Один из самых простых и известных способов вычисления площади четырёхугольника — это разбить его на прямоугольники или треугольники, вычислить площадь каждой части, а затем сложить эти значения. Другой метод, основанный на использовании координат, позволяет найти площадь четырёхугольника, если известны координаты его вершин.
В этой научной статье мы рассмотрим оба этих метода подробнее и приведем наглядные примеры вычисления площади различных типов четырёхугольников. Эти знания помогут вам лучше понять геометрию и упростить вычисления в своих задачах.
Методы вычисления площади четырехугольника
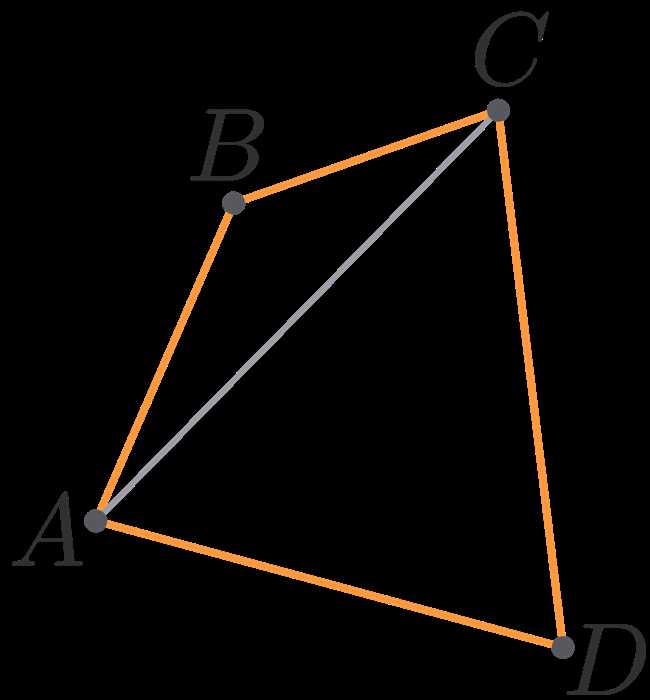
Один из методов — это разделение четырехугольника на треугольники. Если у нас есть возможность разделить фигуру на два или более непересекающихся треугольника, мы можем найти площадь каждого треугольника и сложить их для получения общей площади четырехугольника. Для этого нам понадобится знание длин сторон треугольников и их высот, которые можно найти с помощью теоремы Пифагора или других соотношений между сторонами треугольника.
Другой метод, который можно использовать для вычисления площади четырехугольника, — это использование формулы Гаусса. Формула Гаусса утверждает, что площадь произвольного четырехугольника можно найти, зная длины его сторон и диагоналей. Для этого формула использует полупериметр четырехугольника и длины диагоналей, которые вводятся в формулу как переменные.
В некоторых особых случаях можно использовать более простые формулы для вычисления площади четырехугольника. Например, если четырехугольник является параллелограммом, то его площадь можно найти, умножив длину одной стороны на высоту, опущенную на эту сторону. Также для вычисления площади прямоугольника, который является частным случаем параллелограмма, можно просто перемножить длину двух его сторон.
Таблица с методами вычисления площади четырехугольника:
| Метод | Описание |
|---|---|
| Разделение на треугольники | Четырехугольник разделяется на треугольники, площади которых вычисляются отдельно и затем суммируются |
| Формула Гаусса | Используется формула, основанная на полупериметре и диагоналях четырехугольника |
| Параллелограмм | Если четырехугольник является параллелограммом, его площадь можно найти, умножив длину стороны на высоту |
| Прямоугольник | Площадь прямоугольника можно найти, перемножив длины его сторон |
Необходимо помнить, что точный результат вычислений площади четырехугольника достигается только при наличии точных данных и правильном применении соответствующей формулы или метода. Чтобы избежать ошибок, важно проверить и перепроверить данные и использовать все доступные сведения о фигуре.
Метод вычисления площади по формуле Герона

Вы когда-нибудь задумывались о том, как можно быстро вычислить площадь четырехугольника? Возможно, в вашей жизни возникали ситуации, когда вы сталкивались с такой задачей. Сегодня я расскажу вам об одном из методов вычисления площади четырехугольника, который называется формулой Герона.
Формула Герона — это один из способов вычислить площадь четырехугольника, используя только длины его сторон. Этот метод основан на аналогии с формулой Герона для треугольника, которую вы возможно уже знаете. При этом формула Герона для четырехугольника немного сложнее и требует знания длин всех его сторон.
Если у вас есть четырехугольник со сторонами a, b, c и d, то его площадь можно вычислить по следующей формуле:
S = sqrt((p-a)(p-b)(p-c)(p-d))
где S — площадь четырехугольника,
p — полупериметр четырехугольника, равный (a + b + c + d) / 2, а
sqrt — функция извлечения квадратного корня.
Преимущество формулы Герона заключается в ее простоте и универсальности. Она позволяет вычислить площадь четырехугольника, зная только длины его сторон, без необходимости знания углов или других характеристик. Это делает этот метод удобным и применимым во множестве практических задач.
Для лучшего понимания формулы Герона и ее применения, рассмотрим пример. Предположим, у нас есть четырехугольник со сторонами 5, 6, 7 и 8. Чтобы вычислить его площадь, мы можем воспользоваться формулой Герона:
S = sqrt((p-a)(p-b)(p-c)(p-d))
где a = 5, b = 6, c = 7 и d = 8.
Прежде всего, мы должны вычислить полупериметр p, который равен (a + b + c + d) / 2.
p = (5 + 6 + 7 +  / 2 = 26 / 2 = 13.
/ 2 = 26 / 2 = 13.
Теперь мы можем подставить значения в формулу и рассчитать площадь:
S = sqrt((13-5)(13-6)(13-7)(13-8))
S = sqrt(8 * 7 * 6 * 5)
S = sqrt(1680)
S ≈ 41
Таким образом, площадь данного четырехугольника составляет примерно 41 квадратный сантиметр.
Формула Герона — это мощный и универсальный метод вычисления площади четырехугольника. Он может быть применим во многих ситуациях, где необходимо вычислить площадь четырехугольника, используя только длины его сторон. Надеюсь, что этот метод поможет вам в решении задач и сделает вашу жизнь немного проще!
Метод вычисления площади четырехугольника с диагоналями
Формула Герона была предложена древнегреческим математиком Героном Александрийским и применяется для вычисления площади треугольника. Однако, она также может быть адаптирована для расчета площади четырехугольника с диагоналями.
Для использования формулы Герона необходимо знать длины всех сторон четырехугольника и длины его диагоналей. Если известны только стороны четырехугольника, а диагонали неизвестны, их можно вычислить с использованием теоремы косинусов или теоремы Пифагора.
Основная формула Герона для вычисления площади четырехугольника с диагоналями выглядит следующим образом:
S = √(p — a)(p — b)(p — c)(p — d) -abcd·((cos(∠ACD))2 + (cos(∠CAB))2)
- S — площадь четырехугольника
- a, b, c, d — длины сторон четырехугольника
- p — полупериметр четырехугольника: (a + b + c + d)/2
- ∠ACD, ∠CAB — углы, образованные диагоналями
Определение углов можно выполнить с использованием теоремы косинусов или формулы, связывающей их с длинами сторон четырехугольника.
Зная все необходимые данные, подставляем их в формулу и получаем площадь четырехугольника с диагоналями. Применимость формулы Герона обусловлена ее точностью и простотой использования.
Важно отметить, что вычисление площади четырехугольника с диагоналями может быть сложной задачей, особенно если фигура имеет сложную форму или не все стороны и углы известны. В таких случаях рекомендуется использовать специализированные математические программы или приближенные методы.
Метод вычисления площади четырехугольника по координатам вершин
Вы когда-нибудь задумывались о том, как найти площадь четырехугольника по координатам его вершин? Этот вопрос может показаться сложным, но на самом деле есть простой метод, который позволяет решить эту задачу.
Перед тем, как приступить к вычислениям, необходимо определить тип четырехугольника. Существует несколько видов четырехугольников: прямоугольник, квадрат, ромб, параллелограмм и трапеция. В зависимости от типа четырехугольника, метод вычисления площади может немного отличаться.
Допустим, у нас есть четырехугольник со следующими координатами вершин: A(x1, y1), B(x2, y2), C(x3, y3) и D(x4, y4). Сложим все квадраты разностей координат по очереди: (x1 — x2)^2, (y1 — y2)^2, (x2 — x3)^2, (y2 — y3)^2, (x3 — x4)^2 и (y3 — y4)^2. Затем сложим полученные значения и найдем квадратный корень из этой суммы. Полученное значение будет равно половине площади четырехугольника.
Например, давайте рассмотрим следующий пример. У нас есть четырехугольник ABCD с координатами вершин: A(0, 0), B(0, 4), C(6, 4) и D(6, 0). Применяем описанный метод:
- Считаем разности координат: (0 — 0)^2, (0 — 4)^2, (0 — 6)^2 и (4 — 4)^2.
- Складываем полученные значения: 0 + 16 + 36 + 0 = 52.
- Находим квадратный корень из полученной суммы: √52 ≈ 7.211.
Чтобы найти половину площади четырехугольника, умножим полученное значение на половину одной из сторон, например, на длину стороны AB. В данном примере AB = 4, поэтому площадь четырехугольника ABCD будет равна 7.211 * 4 / 2 = 14.422 квадратных единиц.
Итак, мы научились вычислять площадь четырехугольника по координатам его вершин. Это простой и эффективный метод, который поможет вам решить эту задачу. Теперь вы можете применить его в практических ситуациях, например, при работе с геометрическими фигурами или при решении задач по программированию.
Примеры вычисления площади четырехугольника

Вычисление площади четырехугольника может быть сложной задачей, особенно если фигура имеет сложную форму или включает в себя дополнительные элементы, такие как окружности или эллипсы. Однако, существуют несколько основных методов, которые позволяют нам решить эту задачу.
Во-первых, если все стороны четырехугольника известны, можно использовать формулу Герона, которая основана на полупериметре и длинах сторон. Этот метод особенно полезен для треугольников, но может быть применен и к четырехугольникам, если мы разобьем фигуру на два треугольника.
Во-вторых, для прямоугольников и квадратов площадь можно вычислить, зная длину и ширину. Просто перемножьте эти два значения, и вы получите площадь фигуры.
Третий метод — использование формул для площади трапеции или параллелограмма. Если у вас есть четырехугольник с параллельными сторонами, вы можете использовать эти формулы для вычисления площади.
Четвертый метод — интересный подход, который можно использовать для нерегулярных или сложных четырехугольников — разбить фигуру на более простые фигуры, такие как треугольники или прямоугольники, и затем вычислить площадь каждой из них по отдельности. Затем сложите полученные значения, чтобы получить итоговую площадь.
Независимо от сложности фигуры, вычисление площади четырехугольника может быть важным шагом при решении различных задач и проблем. Понимание разных методов вычисления площади помогает нам лучше понять и воспользоваться этими знаниями в различных ситуациях.






