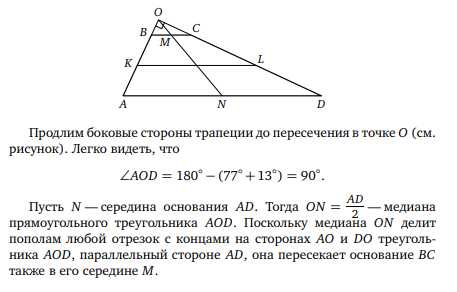
Как найти основания трапеции с углами 77° и 13°? Это вопрос, который может возникнуть у многих учеников при решении геометрических задач. Найдя ответ на этот вопрос, можно решить множество задач, связанных с трапециями. Ответ на вопрос можно найти, применив знания о свойствах трапеции и геометрическом построении углов. Понимая, что сумма углов в треугольнике равна 180°, легко можно установить, что сумма углов в трапеции равна 360°. Зная, что углы при основаниях трапеции являются дополнительными, то есть их сумма равна 180°, можно поставить уравнение и решить задачу, найдя основания трапеции.
Задача: Как найти основания трапеции с углами 77° и 13°?
Чтобы решить эту задачу, нам потребуется знание о свойствах трапеции. Основания трапеции — это стороны, параллельные друг другу. Также в трапеции, сумма углов при основаниях равна 180°. Используя эти свойства, мы сможем найти ответ на нашу задачу.
Давайте начнем с более крупной части трапеции — оснований. Нам известны два угла трапеции — 77° и 13°. Если сумма углов при основаниях равна 180°, то угол, противолежащий первому основанию, будет равен 180° — 77° = 103°. А угол, противолежащий второму основанию, будет равен 180° — 13° = 167°.
Теперь нам известны все углы трапеции: 77°, 13°, 103° и 167°. Вспомни, что сумма углов в четырехугольнике равна 360°. Если мы вычтем из этой суммы сумму углов трапеции (77° + 13° + 103° + 167°), то получим угол в четвертом углу трапеции.
360° — (77° + 13° + 103° + 167°) = 360° — 360° = 0°
Угол в четвертом углу трапеции равен 0°. Это означает, что четвертая сторона трапеции должна быть прямой. Таким образом, основания трапеции являются непараллельными сторонами этой прямой части.
Таким образом, основания трапеции с углами 77° и 13° будут непараллельными сторонами прямолинейной части трапеции. А другими словами, основания трапеции будут сторонами, противолежащими углам 103° и 167°.
Завершая наше путешествие по решению этой задачи, я хотел бы подчеркнуть, что математика, иногда, может быть сложной, но с уверенностью и знанием правил, мы сможем решить любую задачу. Будь настойчивым и не бойся задавать вопросы, и ты сможешь справиться с любыми математическими проблемами!
Условие задачи
Итак, представьте, что вы стоите перед этой задачей. Возможно, у вас возникает некоторое беспокойство или даже страх перед математикой. Но не волнуйтесь, я здесь, чтобы помочь вам разобраться в этой задаче!
Для начала, давайте вспомним некоторые свойства трапеции. Трапеция — это четырехугольник с двумя параллельными сторонами. Основания трапеции важным образом влияют на ее форму и размеры.
Теперь, чтобы найти основания трапеции с заданными углами, мы можем использовать некоторые геометрические свойства и формулы. В данном случае у нас есть два угла: 77° и 13°. Как же нам найти основания по этим углам?
Для начала, обратите внимание на углы при основаниях трапеции. Они называются вершинными углами. Если вы посмотрите на вершинные углы трапеции, вы заметите следующий закон: сумма двух вершинных углов, расположенных по разные стороны от основания, равна 180°. В нашем случае это 77° и 13°, а значит, сумма этих углов также будет равняться 180°.
Теперь давайте продолжим наше рассуждение. У нас есть два угла в трапеции — 77° и 13°, и сумма этих углов равна 180°. Что мы можем сделать с этой информацией? На самом деле, мы можем использовать эту информацию, чтобы найти третий угол трапеции, который равен 180° минус сумма двух известных углов. В нашем случае это будет 180° — (77° + 13°).
Таким образом, третий угол трапеции будет равен 90°. Почему это важно? Потому что третий угол трапеции определяет форму трапеции — если он равен 90°, то это будет прямоугольная трапеция, а если он меньше 90°, то это будет остроугольная трапеция.
Таким образом, зная, что третий угол трапеции равен 90°, мы можем рассмотреть различные случаи и применить соответствующие формулы для нахождения оснований.
Решение:
Для того чтобы найти основания трапеции с заданными углами 77° и 13°, нужно воспользоваться математическими знаниями о геометрии и тригонометрии. Мы можем вспомнить формулы для поиска углов и сторон трапеции.
По определению, трапеция — это четырехугольник, у которого две стороны параллельны, а две другие называются основаниями. Мы знаем, что один основание образует угол в 77°, а другой — 13°.
Для нахождения оснований трапеции мы можем воспользоваться свойствами углов на прямых и свойством суммы углов треугольника. Сумма углов в любом треугольнике всегда равна 180°.
Используя формулу суммы углов в треугольнике, мы можем найти третий угол трапеции, которую мы обозначим как A. Если A + 77° + 13° = 180°, то A = 90°.
Таким образом, мы нашли третий угол трапеции, и он равен 90°. Теперь мы можем использовать свойства трапеции, чтобы найти основания.
Одно из оснований образует угол 77°. Пусть это будет основание AB. Тогда противоположная сторона образует угол 90°, а другое основание (BC) образует угол 13°.
Выражая основание BC через угол 13° и AB, мы можем использовать тригонометрию. Вспомним, что в прямоугольном треугольнике тангенс угла определяется отношением противолежащего катета к прилежащему катету.
Применяя тангенс к углу 13°, мы получаем соотношение:
тангенс 13° = BC / AB
Теперь мы можем найти основание BC, зная основание AB и угол 13°. Не забудьте использовать обратную функцию тангенса, чтобы найти сторону BC:
BC = AB * тангенс 13°
Итак, мы нашли основание BC трапеции, используя тангенс угла 13° и длину основания AB. Теперь у нас есть оба основания трапеции.
Шаг 1: Известные углы
Давайте начнем с более большого угла 77°. Что это за угол? Как вы думаете, может ли он быть прямым углом? Если нет, то какой тип угла наиболее подходит к этому значению? Подумайте, и когда будете готовы, читайте дальше.
Так как прямой угол равен 90°, и у нас имеется угол 77°, который меньше 90°, то мы можем заключить, что наш угол не является прямым. Вместо этого, он меньше и ближе к 90°. Какой же это тип угла? Если вы догадались, что это острый угол, то вы правильно мыслите! Угол 77° — это острый угол.
Теперь перейдем к второму углу — 13°. Какой из типов углов может соответствовать этому значению? Прямой угол? Нет, он больше 90°. Тупой угол? Нет, он больше 180°. Если вы ответили, что это острый угол, то вы абсолютно правы! Угол 13° — это острый угол.
Итак, теперь у нас есть оба известных угла: 77° и 13°, которые оба являются острыми углами. Теперь мы готовы перейти к следующему шагу и найти основания трапеции, используя эти данные.
Шаг 2: Свойства трапеции
Вот основные свойства трапеции:
- Основания трапеции параллельны друг другу.
- Противоположные углы трапеции равны.
- Сумма углов внутри трапеции равна 360 градусов.
Используя эти свойства, мы можем найти основания трапеции с углами 77° и 13°.
Давайте представим, что у нас есть трапеция с основаниями АВ и СD, и с углами А = 77° и С = 13°. Поскольку противоположные углы трапеции равны, у нас также есть углы В и D, которые равны 77° и 13° соответственно.
Мы можем использовать сумму углов внутри трапеции, которая равна 360 градусов, чтобы найти остаточный угол. В данном случае сумма углов А, В, С и D равна 77° + 77° + 13° + 13° = 180°. Остаточный угол равен 360° — 180° = 180°.
Теперь, зная остаточный угол, мы можем использовать свойство трапеции, которое гласит, что сумма углов оснований равна остаточному углу. То есть, углы В и D равны остаточному углу, который равен 180°.
Таким образом, основание АВ трапеции равно основанию СD, и оба они равны остаточному углу 180°.
Итак, основания трапеции со своими углами 77° и 13° равны друг другу и равны 180°.
Шаг 3: Процесс нахождения оснований
Нахождение оснований трапеции с заданными углами 77° и 13° требует применения геометрических методов и формул. Последовательность действий следующая:
- Найдите сумму заданных углов, чтобы убедиться, что она равняется 90°. Если сумма не равна 90°, проверьте правильность введенных данных.
- Найдите значение третьего угла трапеции, используя формулу: 180° — сумма двух заданных углов.
- Примените закон синусов для нахождения длины боковых сторон трапеции. Формула имеет вид: a/sinA = b/sinB, где a и b — стороны трапеции, A и B — соответствующие им углы.
- Найдите длину основания трапеции, используя теорему косинусов. Формула имеет вид: c^2 = a^2 + b^2 — 2ab*cosC, где a и b — боковые стороны, C — угол между ними.
После выполнения этих шагов вы сможете определить длину обоих оснований трапеции с углами 77° и 13°.






