Как найти основание равнобедренного треугольника: математическое решение | Подробное объяснение с формулами

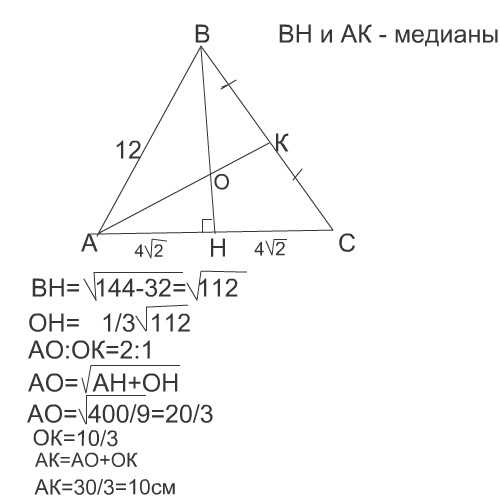
Когда сталкиваешься с задачей на поиск основания равнобедренного треугольника, важно знать математическое решение. Равнобедренный треугольник – это треугольник, у которого две стороны равны друг другу, а угол между ними равен нулю. Чтобы найти основание равнобедренного треугольника, можно использовать свойства этого типа треугольников. Как правило, для решения такой задачи необходимо знать хотя бы одну измеренную сторону треугольника или угол. На практике можно использовать различные методы, такие как применение формул площади треугольника или теоремы косинусов. Важно помнить, что для решения задачи нужно иметь достаточно информации о треугольнике, чтобы определить значение основания.

Основание равнобедренного треугольника: математическое решение

Если вы интересуетесь математикой и задаетесь вопросом о том, как найти основание равнобедренного треугольника, то вы обращаетесь в правильное место! В этой статье мы расскажем вам о математическом решении этой задачи.

Для начала давайте вспомним, что равнобедренный треугольник — это треугольник, у которого две стороны равны. Обычно говорят, что это треугольник, у которого два угла при основании равны.

Возьмем равнобедренный треугольник ABC, где AB = AC. Для удобства, представим, что сторона AB — это основание равнобедренного треугольника.

Чтобы найти длину основания треугольника, нам понадобится знать длину других сторон или углы треугольника. У нас есть несколько методов, которые позволяют нам найти основание:

1. Используя теорему Пифагора
2. Используя теорему косинусов
3. Используя геометрический подход

1. Используя теорему Пифагора

Теорема Пифагора гласит, что для прямоугольного треугольника с катетами a и b и гипотенузой c выполняется соотношение: a^2 + b^2 = c^2.

Таким образом, если мы знаем длину одной из сторон треугольника и гипотенузы, мы можем вычислить длину второй стороны, которая будет являться основанием треугольника.

2. Используя теорему косинусов

Теорема косинусов — это формула, которая позволяет нам определить длину одной стороны треугольника, зная длины двух других сторон и угол между ними. Формула имеет следующий вид: c^2 = a^2 + b^2 — 2ab * cos(C), где c — длина стороны, a и b — длины других сторон, С — угол между этими сторонами.

Используя эту формулу, мы можем вычислить длину одной из сторон треугольника и, зная длину другой стороны, определить длину основания.

3. Используя геометрический подход

Если у вас есть геометрическая задача, вы также можете воспользоваться графическим решением. Нарисуйте равнобедренный треугольник и построьте перпендикуляр к основанию из вершины, где основание пересекает другую сторону. Эта перпендикуляр будет проходить через середину основания и будет одновременно его высотой. Зная длину высоты и зная очевидно, что она равна катету треугольника, мы можем найти длину основания с помощью подобия треугольников.

В завершении хочу сказать, что математика — это удивительная наука, которая дарит нам множество инструментов для решения задач. Зная основные формулы и методы, мы можем решать разнообразные задачи, включая нахождение основания равнобедренного треугольника. Удачи в ваших математических исследованиях!

Математические основы равнобедренных треугольников

Основное свойство равнобедренного треугольника заключается в том, что его основание (третья сторона) является медианой, высотой и биссектрисой одновременно. Это означает, что основание равнобедренного треугольника делит противоположную сторону на две равные части и проходит через центр симметрии треугольника.

Для нахождения длины основания равнобедренного треугольника, можно использовать различные математические методы. Один из них основан на применении теоремы Пифагора. Если известны длины равных сторон треугольника (a), и известна длина основания (b), то можно использовать теорему Пифагора для нахождения b. Для этого нужно возвести в квадрат половину длины основания и вычесть из этого значения квадрат длины одной из равных сторон. Затем извлечь квадратный корень из этого значения.

• Допустим, у нас есть равнобедренный треугольник ABC, где AB = AC = a, BC = b.
• Найдем половину длины основания, обозначим ее как d: d = b/2.
• Возведем длину половины основания в квадрат: d^2.
• Вычтем квадрат длины одной из равных сторон: d^2 — a^2.
• Извлечем квадратный корень из полученного значения: b = √(d^2 — a^2).

Таким образом, мы можем найти длину основания равнобедренного треугольника, зная длины двух равных сторон и применив теорему Пифагора.

Математические основы равнобедренных треугольников позволяют нам легко находить длину основания и использовать их в различных задачах и рассуждениях. Равнобедренные треугольники имеют множество применений в геометрии, физике и других науках. Они являются одним из основных строительных блоков для решения сложных задач и создания сложных структур.

Построение равнобедренного треугольника

Существует несколько способов найти основание равнобедренного треугольника. Некоторые из них мы рассмотрим ниже.

1. Основание равнобедренного треугольника через высоту и боковую сторону

Если известны высота равнобедренного треугольника и длина одной из его боковых сторон, то основание можно найти с помощью теоремы Пифагора.

Допустим, у нас есть высота треугольника и длина одной из его боковых сторон. Зная высоту, можно найти площадь треугольника, а затем с помощью формулы площади треугольника S = 1/2 * a * h найти основание, где a — длина одной из боковых сторон, h — высота.

Пример: У нас есть равнобедренный треугольник с высотой h = 6 и длиной боковой стороны a = 8. Площадь треугольника равна S = 1/2 * 8 * 6 = 24. Для равнобедренного треугольника площадь можно найти и по формуле S = 1/2 * a * b, где a и b — боковые стороны треугольника. Так как у нас две равные стороны, то a = b, и тогда площадь можно найти как S = 1/2 * a * a = 1/2 * a^2. Итак, у нас получается уравнение 1/2 * a^2 = 24. Решаем его и находим a = √(2 * 24) = √48 = 4√3. Таким образом, основание равнобедренного треугольника равно 4√3.

2. Основание равнобедренного треугольника через угол

Если нам известен угол при основании равнобедренного треугольника, то основание можно найти с помощью тригонометрии. Для этого нам понадобится функция тангенс. Формула будет следующей: a = 2 * h * tg(α/2), где a — основание, h — высота, α — угол при основании.

Пример: Пусть у нас есть равнобедренный треугольник с углом при основании α = 60° и высотой h = 5. Используя формулу, находим a = 2 * 5 * tg(60°/2) = 2 * 5 * tg(30°) = 2 * 5 * (√3/3) = 10 * √3/3. Таким образом, основание равнобедренного треугольника равно 10 * √3/3.

3. Основание равнобедренного треугольника через радиус вписанной окружности

Если нам известен радиус вписанной окружности равнобедренного треугольника, то основание можно найти с помощью формулы a = 2 * r * sin(α/2), где a — основание, r — радиус вписанной окружности, α — угол при основании.

Пример: Пусть у нас есть равнобедренный треугольник с радиусом вписанной окружности r = 5 и углом при основании α = 45°. Используя формулу, находим a = 2 * 5 * sin(45°/2) = 10 * sin(22.5°) ≈ 10 * 0.3827 ≈ 3.827. Таким образом, основание равнобедренного треугольника примерно равно 3.827.

В итоге, чтобы найти основание равнобедренного треугольника, можно использовать различные методы, такие как нахождение по высоте и боковой стороне, по углу при основании или радиусу вписанной окружности. Выберите тот метод, который наиболее удобен и подходит к вашей задаче. Удачи в построении равнобедренных треугольников!

Формула для нахождения основания равнобедренного треугольника

Формула для нахождения основания равнобедренного треугольника выглядит следующим образом:

Основание = (Периметр — 2 x Длина равных сторон) / 2

Чтобы применить эту формулу, необходимо знать периметр треугольника и длину равных сторон. Периметр равнобедренного треугольника можно найти, сложив длины всех его сторон. Длина равных сторон равнобедренного треугольника известна и равна одному и тому же значению.

Используя эту формулу, вы сможете легко и быстро найти основание равнобедренного треугольника, что может быть полезно в решении различных задач и упражнений по геометрии. Надеюсь, данная информация окажется полезной для вас!