- Как найти объём куба по диагонали: формула и основные принципы вычисления
- Различные методы определения диагонали куба
- Метод измерения с помощью линейки
- Метод использования формулы для объема куба
- Метод с использованием трех измерений
- Метод с использованием геометрического построения
- Метод с использованием диаграммы
- Метод с использованием опыта
- Использование формулы для вычисления диагонали
- Измерение диагонали с помощью инструментов
- Лента
- Лазерный измеритель
- Ультразвуковой измеритель
- Подводя итоги
- Примеры расчета объема куба по диагонали
- Пример 1:
- Пример 2:
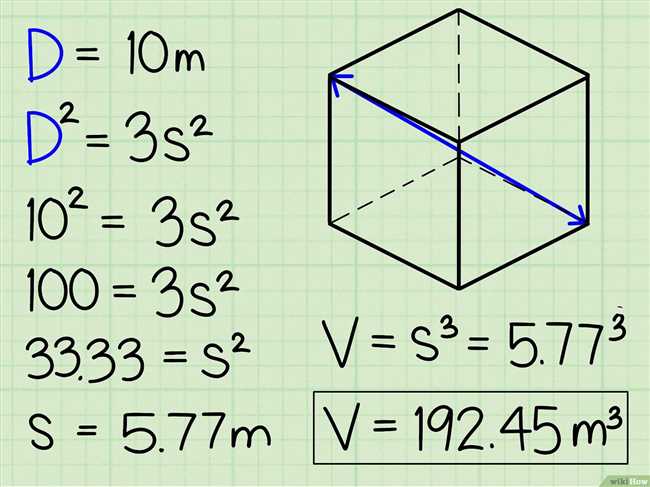
- Расчёт объёма куба по известной длине диагонали
- Расчёт длины диагонали по известному объёму куба
Когда мы говорим о поиске объема куба, ключевым понятием является его диагональ. Диагональ — это линия, соединяющая любые две вершины куба. Чтобы найти объем куба по его диагонали, существует специальная формула.
Формула для нахождения объема куба по диагонали состоит из следующих шагов:
1. Найдите длину одной стороны куба. Для этого можно использовать теорему Пифагора.
2. Возведите длину стороны куба в куб и получите объем.
Давайте рассмотрим пример: если диагональ куба равна 10 сантиметрам, то каждая сторона будет равна 7,07 сантиметров, а объем куба — 343 сантиметра кубического.
Использование данной формулы позволяет найти объем куба и использовать его в различных научных расчетах.
Как найти объём куба по диагонали: формула и основные принципы вычисления
Перед тем, как мы перейдем к формуле, давайте вспомним основные принципы вычисления объема куба. Первым принципом является то, что все стороны куба равны друг другу. Например, если одна сторона куба равна 5 сантиметров, то все стороны куба равны 5 сантиметрам.
Итак, теперь мы готовы перейти к формуле. Формула для вычисления объёма куба по его диагонали следующая:
Объём куба = (Длина диагонали^3) / (3√2)
Вы, наверное, задаетесь вопросом, откуда возникает эта формула? Начнем с того, что диагональ куба — это отрезок, который соединяет две противоположные вершины куба. Он также является диагональю боковой грани куба.
Теперь изображим этот отрезок как гипотенузу прямоугольного треугольника, а стороны куба — как его катеты. Поскольку все стороны куба равны между собой, то мы можем сказать, что каждый катет треугольника равен a (длине стороны куба).
Далее, применяя теорему Пифагора (a^2 + a^2 = диагональ^2), мы можем найти длину катета:
a = диагональ / √2
Теперь, чтобы найти объем куба, мы можем использовать стандартную формулу для объёма прямоугольного параллелепипеда, потому что куб — это особый случай прямоугольного параллелепипеда, когда все стороны равны.
Итак, формула для объёма куба по его диагонали:
Объём куба = a^3 = (Длина диагонали / √2)^3 = (Длина диагонали^3) / (3√2)
Вот и все! Теперь вы знаете, как найти объём куба по его диагонали. Пользуйтесь этой формулой и вычисляйте объемы кубов без проблем. На практике мы можем использовать эту формулу для вычисления объемов кубов, используя диагонали, которые нам известны.
Различные методы определения диагонали куба
Если вы заинтересованы в определении диагонали куба, то у вас есть несколько методов для измерения этого параметра. В данной статье я расскажу о нескольких из них, чтобы помочь вам разобраться в этом вопросе.
Метод измерения с помощью линейки
Самым простым и доступным способом определения диагонали куба является использование обычной линейки. Для этого нужно измерить каждую из сторон куба и затем применить теорему Пифагора. Согласно этой теореме, квадрат диагонали равен сумме квадратов каждой из сторон куба. Таким образом, вы можете вычислить длину диагонали, взяв квадратный корень от этой суммы.
Метод использования формулы для объема куба
Другим способом определения диагонали куба является использование формулы для объема. Объем куба равен третьей степени его стороны. Таким образом, если вы знаете объем куба, вы можете вычислить длину его стороны, а затем произвести вычисление диагонали, используя теорему Пифагора.
Метод с использованием трех измерений
Если у вас есть физический куб, то вы можете воспользоваться трехмерной системой координат для определения его диагонали. Для этого нужно измерить расстояние между двумя противоположными углами куба в трех измерениях — длина, ширина и высота. Затем вы можете использовать формулу для вычисления длины трехмерного вектора, чтобы получить длину диагонали куба.
Метод с использованием геометрического построения

Если вам интересно узнать диагональ куба на основе его рёбер, вы можете воспользоваться геометрическим построением. Для этого нужно нарисовать плоскость, проходящую через два противоположных ребра куба, и найти пересечение этой плоскости с противоположным ребром. Затем, путем измерения этого перпендикуляра, вы сможете определить диагональ куба.
Метод с использованием диаграммы
Если вы не понаслышке знакомы с компьютерной графикой, то смешанный графический метод будет оптимальным для вас. Вам потребуется программа для создания трехмерных моделей либо математическому пакету программ или же, вы можете воспользоваться онлайн-сервисом. Нарисуйте куб в программе и нарисуйте диагональ на вашем изображении. Затем вы можете с помощью инструментов программы измерить длину этой диагонали.
Метод с использованием опыта
Если у вас есть абсолютно точные измерения длины, ширины и высоты куба, а также его объема, то вы можете разделить объем на площадь основания, чтобы получить высоту. Затем вы можете использовать теорему Пифагора для вычисления длины диагонали. Если вы хорошо знакомы с основными принципами геометрии и имеете некоторый опыт в использовании математики, то этот метод может быть лучшим для вас.
Теперь, когда вы знакомы с различными методами определения диагонали куба, вы можете выбрать подходящий для вас и приступить к вычислениям. Не забывайте использовать правильные формулы и уточнять данные, чтобы получить точные результаты!
Использование формулы для вычисления диагонали
Для начала, давайте вспомним, что диагональ — это отрезок, соединяющий две противоположные вершины куба. Каждая сторона куба является равным отрезком. Пусть a будет длиной стороны куба.
Теперь, чтобы найти диагональ куба, мы можем использовать теорему Пифагора, которая гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. В нашем случае, диагональ куба — гипотенуза, а сторона — это катет.
Таким образом, формула для вычисления диагонали куба будет:
Диагональ = √(a² + a² + a²) = √3a
Теперь, давайте рассмотрим пример расчета диагонали. Предположим, что у нас есть куб со стороной длиной 5 см. Чтобы найти его диагональ, мы можем использовать формулу:
Диагональ = √3a
Диагональ = √3(5) = √75 ≈ 8.66 см
Таким образом, диагональ этого куба составляет около 8.66 см.
Из этого примера ясно, что вычисление диагонали куба с использованием формулы не так сложно. Эта формула очень полезна в различных отраслях, таких как архитектура, инженерия и строительство. Понимание и применение этой формулы помогут вам решать задачи, связанные с вычислениями диагоналей трехмерных объектов.
Измерение диагонали с помощью инструментов
Измерение диагонали может быть важным шагом для определения объема куба. Но каким инструментом можно достичь максимальной точности? Давайте рассмотрим несколько вариантов и определим, какой метод будет для вас наиболее удобным.
Лента
Одним из самых распространенных инструментов для измерений является лента. Она проста в использовании и доступна практически каждому. Для измерения диагонали куба, возможно, придется использовать ленту с длинной, которую можно непрерывно вытянуть. Помните, что лента должна быть обернута вокруг диагонали, а не просто проведена через куб. Будьте внимательны и аккуратны при проведении измерения для получения наиболее точного результата.
Лазерный измеритель
Если нужна еще более точная мера диагонали, можно воспользоваться лазерным измерителем. Этот инструмент работает с помощью лазерного луча, который измеряет расстояние от одной точки до другой. Он может быть полезен при измерении диагонали куба, так как обеспечивает высокую точность измерений. Просто направьте лазерный измеритель на две противоположные точки на диагонали куба и получите точные данные о его длине.
Ультразвуковой измеритель
Еще одним вариантом инструмента для измерения диагонали может быть ультразвуковой измеритель. Он работает на основе отражения звуковых волн от объекта и измеряет время, за которое звук проходит до объекта и возвращает обратно. Ультразвуковые измерители обеспечивают точные результаты и могут быть полезны при измерении длины диагонали куба.
Подводя итоги
Итак, для измерения диагонали куба можно использовать различные инструменты, такие как лента, лазерный измеритель или ультразвуковой измеритель. Каждый из этих инструментов обеспечивает определенную степень точности и удобства использования. Выбор конкретного инструмента зависит от ваших предпочтений и доступности. Независимо от того, какой инструмент вы выбираете, помните о том, чтобы быть аккуратными и внимательными при измерении диагонали куба, чтобы получить наиболее точные результаты.
Примеры расчета объема куба по диагонали
Узнать объем куба по его диагонали может быть полезно в различных ситуациях, например, при планировании использования пространства или при решении задач геометрии. Для расчета объема куба по диагонали есть специальная формула.
Формула для расчета объема куба по диагонали имеет вид:
V = (d^3) / (3√2)
Где V — объем куба, а d — диагональ куба. С помощью этой формулы можно рассчитать объем куба, зная его диагональ. Давайте рассмотрим несколько примеров расчета.
Пример 1:
Предположим, что у нас есть куб с диагональю 10 см. Чтобы найти его объем, мы подставляем значение диагонали в формулу:
V = (10^3) / (3√2)
V = 1000 / (3√2)
Рассчитываем корень из 2:
√2 ≈ 1.41
Подставляем значение и округляем ответ:
V ≈ 1000 / (3 * 1.41)
V ≈ 1000 / 4.23
V ≈ 236.71
Таким образом, объем куба с диагональю 10 см составляет около 236.71 кубических сантиметров.
Пример 2:
Предположим, что у нас есть куб с диагональю 5 метров. Чтобы найти его объем, мы снова подставляем значение диагонали в формулу:
V = (5^3) / (3√2)
Рассчитываем корень из 2:
√2 ≈ 1.41
Подставляем значение и округляем ответ:
V ≈ 125 / (3 * 1.41)
V ≈ 125 / 4.23
V ≈ 29.55
Таким образом, объем куба с диагональю 5 метров составляет около 29.55 кубических метров.
Важно помнить, что расчеты объема куба по диагонали могут быть приближенными, так как формула использует некоторые оценки и приближения. Однако, в большинстве случаев эти приближения достаточно точны для практического использования. Теперь вы знаете, как рассчитать объем куба по его диагонали!
Расчёт объёма куба по известной длине диагонали
Вы когда-нибудь задумывались, как найти объём куба, зная лишь длину его диагонали? Не переживайте, я помогу вам разобраться в этом вопросе.
Для начала, вспомним основные характеристики куба. Как вы знаете, куб – это специальный вид прямоугольного параллелепипеда, все его стороны равны друг другу и образуют прямые углы между собой.
Чтобы облегчить расчёты, предположим, что длина диагонали куба известна и равна d.
Для определения объёма куба, мы можем воспользоваться формулой для объёма прямоугольного параллелепипеда:
Объём = a³
Здесь a – длина стороны куба.
Чтобы найти длину стороны куба, нужно использовать свойство прямоугольного треугольника, в котором гипотенуза (диагональ куба) равна корню квадратному из суммы квадратов катетов. В нашем случае оба катета равны длине стороны куба, поэтому мы можем записать:
a = √(d²/2)
Используя эту формулу, мы можем найти длину стороны куба и, затем, подставить её в формулу для объёма, чтобы получить окончательное значение объёма куба.
Теперь рассмотрим пример расчета. Предположим, что длина диагонали куба равна 8 единицам.
Применим формулу: a = √(8²/2) = √(64/2) = √32 ≈ 5.66
Теперь, подставим найденное значение длины стороны куба в формулу для объема: Объем = 5.66³ ≈ 181.03
Таким образом, объем куба с диагональю длиной 8 единиц примерно равен 181.03 единицам объема.
Теперь, когда вы знаете формулу и принцип расчета объема куба по известной длине его диагонали, вы сможете справиться с подобными задачами со свистом. Это очень полезное знание, которое может быть применено во множестве ситуаций, например, при решении задач в геометрии или в строительстве.
Надеюсь, что данная информация оказалась полезной для вас! Если у вас возникли какие-либо вопросы или у вас остались трудности с расчетом, не стесняйтесь обращаться ко мне в любое время. Я всегда готов помочь!
Расчёт длины диагонали по известному объёму куба
Для научных исследований, а также в реальной жизни, часто возникает необходимость рассчитать длину диагонали куба по известному объёму. Эта задача может быть решена с помощью простой формулы и нескольких примеров расчёта.
Формула для расчёта длины диагонали куба (d) по известному объёму (V) выглядит следующим образом:
d = ∛(√2 * V)
Где ∛ обозначает взятие кубического корня, а √2 — квадратный корень из 2.
Давайте рассмотрим несколько примеров расчёта диагонали по известному объёму:
-
Пример 1:
Пусть объём куба равен 64 кубическим сантиметрам:
Рассчитываем длину диагонали по формуле:
d = ∛(√2 * 64) = ∛(8√2) ≈ 4.612
Таким образом, длина диагонали куба составляет примерно 4.612 сантиметра.
-
Пример 2:
Пусть объём куба равен 125 кубическим метрам:
Рассчитываем длину диагонали по формуле:
d = ∛(√2 * 125) = ∛(25√2) ≈ 9.524
Таким образом, длина диагонали куба составляет примерно 9.524 метра.
Таким образом, используя данную формулу и приведённые примеры расчёта, можно легко рассчитать длину диагонали куба по известному объёму. Этот метод поможет как в научных исследованиях, так и в повседневной жизни.






