
Когда нам необходимо найти все делители числа, мы часто знаем несколько способов для этого. Однако, что делать, если мы сталкиваемся с ситуацией, когда число неизвестно, а найти все его делители необходимо? Существуют несколько простых способов, которые позволяют решить эту задачу. Один из способов — это факторизация числа. Отличительной чертой данного метода является разложение числа на простые множители и нахождение всех возможных комбинаций этих множителей. Таким образом, мы получаем все возможные делители данного числа. Еще одним способом является перебор всех чисел от 1 до самого числа. При этом мы проверяем, делится ли число на каждое из этих чисел без остатка. Если да, то данное число является делителем нашего числа. Используя эти простые способы, мы можем легко найти все делители неизвестного числа.
Основы поиска неизвестного делителя
Метод перебора
Наиболее простым и интуитивным способом поиска делителя является метод перебора. Он состоит в последовательной проверке каждого числа от 2 до самого числа на делимость. Если находим число, которое делит заданное число без остатка, то это и есть искомый делитель.
Например, пусть мы ищем делитель для числа 20. Начинаем перебирать числа с 2. Первое число, которое делит 20 без остатка, — это 2. Таким образом, мы нашли делитель для числа 20.
Метод перебора является наиболее простым, но может потребоваться много времени на проверку больших чисел. Тем не менее, в некоторых случаях он может быть полезным для быстрого нахождения делителя.
Факторизация
Еще одним эффективным методом поиска делителя является факторизация числа. Он заключается в разложении числа на простые множители, а затем нахождении делителей путем комбинирования этих множителей.
Например, пусть мы ищем делитель для числа 36. Сначала факторизуем его: 36 = 2 * 2 * 3 * 3. Затем комбинируем эти множители, чтобы найти делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18 и 36.
Факторизация является более эффективным методом, чем метод перебора, особенно для больших чисел, так как он позволяет найти все делители числа с меньшим количеством проверок.
Метод двоичного поиска
Если вы знаете примерное значение делителя, вы можете воспользоваться методом двоичного поиска, чтобы быстро найти точное значение. Этот метод основан на разделении возможных значений делителя пополам и последовательном сужении диапазона до нахождения правильного значения.
Например, если мы знаем, что делитель числа находится в диапазоне от 1 до 100, мы можем начать с середины диапазона (50) и проверить, является ли это число делителем. Если да, то мы получили искомый делитель. Если нет, то мы можем сужать диапазон до половины и повторять процесс.
Метод двоичного поиска позволяет быстро находить делитель, особенно если у вас есть некоторая информация о примерном значении делителя.
Таблица делителей
Если у вас есть набор чисел, для которых нужно найти общий делитель, вы можете использовать таблицу делителей. В этой таблице вы указываете делители для каждого числа и затем ищете общие делители.
Например, пусть у нас есть числа 12, 18 и 24. Составляем таблицу делителей для каждого числа:
| Число | Делители |
|---|---|
| 12 | 1, 2, 3, 4, 6, 12 |
| 18 | 1, 2, 3, 6, 9, 18 |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 |
Ищем общие делители для всех чисел в таблице: 1, 2, 3 и 6. Эти числа являются общими делителями для всех трех чисел.
Таблица делителей помогает быстро и удобно находить общие делители для набора чисел, так как все делители сгруппированы в одном месте.
Теперь, когда у вас есть базовые знания о методах поиска неизвестного делителя, вы можете применять их для решения различных математических задач. Не бойтесь экспериментировать и искать новые подходы — это поможет вам стать лучшим в решении задач по поиску делителей.
Перебор делителей
Для начала, давайте рассмотрим пример. Предположим, что мы хотим найти все делители числа 12.
Первым делителем будет число 1. Проверим, делится ли 12 на 1 без остатка. Очевидно, что да.
Затем мы переходим к следующему числу — 2. Делится ли 12 на 2 без остатка? Опять же, да. Таким образом, 2 также является делителем числа 12.
Продолжая этот процесс, мы переходим к числу 3. Однако, 12 не делится на 3 без остатка. Таким образом, 3 не является делителем числа 12.
Мы продолжаем и переходим к числу 4. Делится ли 12 на 4 без остатка? Да, делится.
Затем мы проверяем число 5. Однако 12 не делится на 5 без остатка.
Мы продолжаем и переходим к числу 6. Опять же, 12 делится на 6 без остатка.
И, наконец, проверяем число 7. Но, как и предыдущие числа, 12 не делится на 7 без остатка.
Таким образом, все делители числа 12 это 1, 2, 3, 4 и 6.
В данном примере мы рассмотрели только числа до 7, но на самом деле, чтобы найти все делители числа, нужно перебрать все числа от 1 до самого числа.
Хоть этот метод и простой, он эффективен только для небольших чисел. Когда мы имеем дело с очень большими числами, перебор может занять слишком много времени и ресурсов.
Также стоит отметить, что делители числа всегда идут парами. Например, если 12 делится на 2 без остатка, то оно также делится на 6 без остатка. Таким образом, перебор делителей можно сократить до квадратного корня исходного числа.
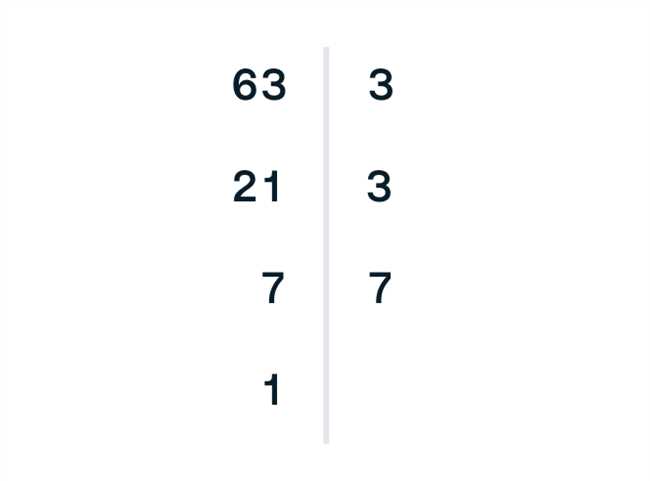
Факторизация числа

Факторизация числа является важной математической операцией, которая помогает нам понять структуру и свойства чисел. Разложение числа на простые множители позволяет нам лучше его изучать и использовать в различных задачах.
Факторизацию чисел можно проводить как вручную, так и с помощью компьютерных программ. Процесс факторизации может быть довольно сложным, особенно для больших чисел, но существуют различные методы, которые позволяют упростить этот процесс.
Упрощение процесса факторизации возможно, если использовать некоторые техники, такие как:
- Правило нахождения простых делителей: для поиска простых делителей числа достаточно проверить все целые числа от 2 до квадратного корня из этого числа.
- Метод деления на простые числа: данный метод заключается в поочередном делении числа на простые числа, пока не получится простое число или 1.
- Метод сокращенного возведения в степень: данный метод позволяет быстро факторизовать числа, имеющие определенную структуру.
Факторизация числа играет важную роль в криптографии, алгоритмах шифрования и других областях науки. Правильное факторизирование числа может помочь нам решить различные задачи более эффективно и точно.
Использование алгоритма Евклида
Итак, как мы можем использовать алгоритм Евклида для поиска неизвестного делителя? Допустим, у нас есть два числа – число «a» и число «b». Мы хотим найти наибольший общий делитель этих двух чисел. Алгоритм Евклида позволяет нам сделать это достаточно быстро.
Сам алгоритм Евклида основан на простой идеи: если «a» делится на «b» без остатка, то «b» является наибольшим общим делителем, и поиск можно считать завершенным. Если же «a» не делится на «b» без остатка, мы выполняем следующие шаги:
- Находим остаток от деления «a» на «b». Это можно сделать с помощью операции деления с остатком.
- Присваиваем «a» значение «b», а «b» получает значение найденного остатка.
- Повторяем шаги 1 и 2 до тех пор, пока «a» не станет делиться на «b» без остатка.
Как только алгоритм заканчивает свою работу, значение «b» становится наибольшим общим делителем чисел «a» и «b».
Попробуйте реализовать алгоритм Евклида на практике, чтобы найти неизвестный делитель. Задайте два числа и следуйте алгоритму. Вы удивитесь, насколько просто и эффективно можно найти наибольший общий делитель.
Алгоритм Евклида является основой для многих других математических и компьютерных алгоритмов. Он широко используется в криптографии, численных методах и других областях. Поэтому понимание и использование этого алгоритма может быть полезным и интересным.
Применение алгоритма поиска наибольшего общего делителя
Алгоритм поиска НОД основан на принципе нахождения остатка от деления. Он представляет собой последовательное нахождение остатка от деления двух чисел и замену этих чисел на делитель и остаток. Процесс повторяется до тех пор, пока не будет найден делитель, равный нулю. Затем НОД будет равен последнему делителю.
Применение алгоритма поиска НОД позволяет эффективно находить наибольший общий делитель двух чисел без необходимости проверки каждого возможного делителя. Этот алгоритм имеет линейную сложность и может быть применен как для небольших, так и для больших чисел. Он широко используется в различных областях, включая криптографию, арифметику и теорию чисел.
Алгоритм поиска НОД является одним из ключевых инструментов при решении задач, связанных с поиском делителей чисел. Он предоставляет удобный и эффективный способ нахождения наибольшего общего делителя и может быть использован во множестве ситуаций. Знание этого алгоритма является важным для программистов и математиков, работающих с числами и вычислениями.






