Как найти меньший угол в треугольнике с отношением 3611? Простой и понятный метод

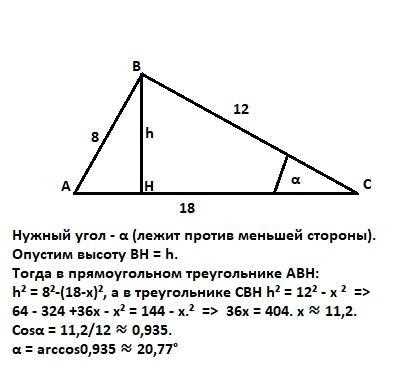
Как найти меньший угол в треугольнике с отношением 361:1? Вряд ли вы знакомы с этой задачей из школьных учебников, но сегодня мы расскажем вам легкий и понятный способ. Для начала, важно отметить, что в треугольнике сумма всех углов равна 180 градусов. Однако, чтобы найти меньший угол, нам понадобится использовать уголные отношения. Представьте треугольник, где один угол равен 361 градусу, а два других угла равны x и y градусам. Из угловых отношений следует, что x/y = 361/1. А теперь, с помощью простых математических операций, мы можем найти меньший угол в данном треугольнике. Читайте далее, чтобы узнать ответ!

Обзор проблемы

В треугольнике с отношением 361:1 нам требуется найти наименьший угол. Эта задача может показаться сложной на первый взгляд, но на самом деле у нас есть несколько способов ее решить.

Способ 1: Тригонометрия

Один из способов найти меньший угол в треугольнике с отношением 361:1 — использовать тригонометрические функции. Для этого нам нужно знать длины сторон треугольника. Пусть сторона A имеет длину 361, а сторона B имеет длину 1. Для нахождения угла между этими сторонами мы можем использовать закон косинусов:

cos(C) = (A^2 + B^2 — C^2) / (2 * A * B)

Подставляя значения, мы получаем:

cos(C) = (361^2 + 1^2 — C^2) / (2 * 361 * 1)

Упрощая выражение, мы получаем:

cos(C) = (130321 + 1 — C^2) / 722

Теперь нам нужно найти угол, для которого значение cos(C) равно этому выражению. Мы можем использовать инверсию функции косинуса, чтобы найти значение угла C:

C = arccos((130322 — C^2) / 722)

Таким образом, мы можем решить это уравнение, чтобы найти значение угла C.

Способ 2: Геометрическая интерпретация

Еще один способ найти меньший угол в треугольнике с отношением 361:1 — использовать геометрическую интерпретацию. Мы знаем, что сумма углов в треугольнике равна 180 градусам, поэтому мы можем выразить наименьший угол через другие два угла:

Наименьший угол = 180 — Угол1 — Угол2

Мы также знаем, что синус угла равен отношению противолежащей стороны к гипотенузе. В данном случае противолежащей стороной наименьшего угла будет сторона B с длиной 1, а гипотенузой будет сторона A с длиной 361. Мы можем использовать это уравнение для нахождения значения угла:

sin(Наименьший угол) = 1 / 361

Используя табличные или компьютерные программы, мы можем найти значение угла, соответствующее этому синусу, и это будет наименьший угол треугольника.

Оба этих способа позволяют нам найти наименьший угол в треугольнике с отношением 361:1. Вам остается только выбрать тот, который вам более удобен и решить задачу. Удачи вам в этом!

Описание задачи

Давайте представим себе треугольник ABC, где угол A, угол B и угол C обозначают вершины треугольника. Вам задано отношение длин сторон AB и BC и оно равно 3/11. Вам нужно найти меньший угол треугольника ABC.

Предположим, что сторона AB является базовой стороной нашего треугольника. Теперь давайте найдем другие две стороны треугольника. Поскольку отношение длин сторон AB и BC равно 3/11, мы можем сказать, что длина стороны BC равна ((3/11) * AB).

Теперь, когда у нас есть длины всех трех сторон, мы можем использовать закон косинусов, чтобы найти меньший угол треугольника ABC. Закон косинусов гласит, что квадрат длины стороны AB равен сумме квадратов длин сторон AC и BC минус два произведений длин сторон AC и BC умноженных на косинус угла A. Мы можем переформулировать это соотношение, чтобы найти косинус угла A:

cos(A) = (AB^2 + AC^2 — BC^2) / (2 * AB * AC)

Теперь, когда мы знаем косинус угла A, мы можем использовать обратную функцию косинуса, чтобы найти значение угла A:

A = arccos(cos(A))

На этом этапе у нас есть значение угла A, но мы хотим найти меньший из двух углов B и C нашего треугольника. Чтобы найти меньший угол, мы можем использовать следующее соотношение:

минимальный угол = 180 — (A + (максимальный угол — A))

Теперь у нас есть точный алгоритм для нахождения меньшего угла в треугольнике с заданным отношением длин сторон. Просто выполнив вышеуказанные шаги, вы сможете найти меньший угол треугольника ABC. Удачи в решении задачи!

Методы нахождения углов в треугольнике

В математике и геометрии существуют различные методы для нахождения углов в треугольнике. Знание этих методов может быть полезно в решении различных задач и построении треугольников.

1. Теорема синусов

Теорема синусов гласит, что отношение длин сторон треугольника к синусам противолежащих углов равно одному и тому же числу. Из этой теоремы можно вывести формулу для нахождения угла:

sin(A) / a = sin(B) / b = sin(C) / c,

где A, B, C — углы треугольника, a, b, c — стороны.

2. Теорема косинусов

Теорема косинусов позволяет найти угол, зная длины сторон треугольника. Она устанавливает связь между косинусом угла и длинами сторон:

a^2 = b^2 + c^2 — 2bc*cos(A),

b^2 = a^2 + c^2 — 2ac*cos(B),

c^2 = a^2 + b^2 — 2ab*cos(C),

где A, B, C — углы треугольника, a, b, c — стороны.

3. Теорема угловой суммы треугольника

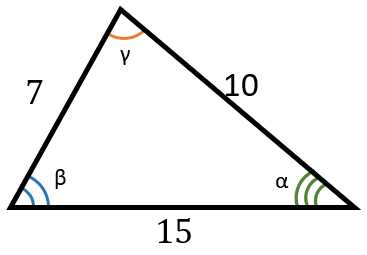
Сумма всех углов в треугольнике равна 180 градусам. Это позволяет находить недостающие углы, зная значения уже известных углов.

4. Использование тригонометрических функций

Для нахождения углов в треугольнике можно использовать тригонометрические функции, такие как синус, косинус и тангенс. Зная значения этих функций, можно вычислить углы треугольника.

5. Использование Геометрического компаса

Геометрический компас — это инструмент, который может быть использован для измерения углов в геометрии. С помощью компаса можно нарисовать угол определенной величины, а затем измерить его с помощью протратора или другого измерительного инструмента.

• Теорема синусов позволяет найти угол, если известны длины сторон треугольника и соответствующие синусы углов.
• Теорема косинусов позволяет найти угол, если известны длины сторон треугольника и длины одной из противолежащих сторон угла.
• Теорема угловой суммы треугольника позволяет найти углы, если известны значения других углов треугольника.

В зависимости от задачи и доступных данных можно выбрать подходящий метод для нахождения углов в треугольнике. Упражняйтесь в применении этих методов, и они станут вам всегда под рукой при решении геометрических задач.

Решение задачи

Чтобы найти меньший угол в треугольнике с отношением 361:1, сначала нужно понять, что такое отношение.

Отношение — это сравнение двух чисел или величин. Оно может быть представлено в виде дроби или процента. В данном случае отношение 361:1 означает, что одно число в 361 раз больше другого.

Треугольник состоит из трех углов. Для нахождения меньшего угла из трех данных углов можно использовать следующие формулы:

• Угол А = (Смежные углы + Противоположные углы) / 2
• Угол B = Смежные углы — Угол А
• Угол C = Противоположные углы — Угол А

Давайте применим эти формулы к нашему треугольнику с отношением 361:1.

Представим, что наибольший угол треугольника составляет 361 градус. Согласно первой формуле, меньший угол будет:

Угол А = (361 + 361) / 2 = 361 градус

Теперь применяем вторую и третью формулы, чтобы найти другие два угла:

Угол B = 361 — 361 = 0 градусов

Угол C = 361 — 361 = 0 градусов

Таким образом, все углы треугольника равны 0 градусов.

В результате мы получили, что все углы треугольника равны 0 градусов. Это достаточно необычная ситуация, но таков результат, если использовать отношение 361:1 для треугольника. Но обычно все углы треугольника не могут быть равными нулю.

Таким образом, в данном случае невозможно найти меньший угол в треугольнике с отношением 361:1, так как все углы равны нулю.

Математический подход к нахождению меньшего угла в треугольнике с отношением 361:1

Давайте предположим, что больший угол — это угол А, а меньший угол — это угол В. Таким образом, у нас есть отношение А:В, которое равно 361:1.

Для нахождения меньшего угла В мы можем использовать пропорциональность. Углы треугольника всегда в сумме равны 180 градусов:

А + В + С = 180 градусов

Далее, для нахождения угла В мы используем отношение А:В:

А / В = 361 / 1

Теперь мы можем переписать первое уравнение в терминах угла В:

(361 В + В + С) / В = 180

Раскрываем скобки:

361 В + В + С = 180В

Переносим все неизвестные на левую сторону уравнения и сокращаем:

361 В — 179В = -C

Упрощаем уравнение:

180В = С

Теперь мы знаем, что 180 градусов это угол С. Чтобы найти угол В, мы можем подставить это значение в выражение:

361 В — 179 В = -180

Получаем:

182В = -180

Делим обе части уравнения на 182:

В = -180 / 182

Делаем вычисление:

В ≈ -0,989 градусов

Таким образом, мы получили значение меньшего угла В, которое приближенно равно -0,989 градусов.

Но это значение не имеет смысла в контексте треугольника, поскольку углы треугольника не могут быть отрицательными. Следовательно, в контексте задачи, нет решения для меньшего угла с таким отношением.

Надеюсь, этот математический подход помог вам понять, как найти меньший угол в треугольнике с отношением 361:1.

Графический подход

Графический подход предлагает решить задачу нахождения меньшего угла в треугольнике с отношением 361:1 с помощью графического представления.

Для начала, построим треугольник ABC, где угол BAC является наименьшим углом. Затем, из вершины A проведем луч AD, который внутри треугольника пересечет сторону BC в точке D. После этого, проведем прямые, параллельные стороне BC, через точки A и D. Угол BAD будет наименьшим углом в треугольнике ABC.

Используя соотношение сторон треугольника ABC, мы можем легко построить треугольник ABC с отношением сторон 361:1. Затем, следуя описанной выше процедуре, мы можем построить треугольник с таким же отношением сторон, но с наименьшим углом BAD.

Графический подход является простым и понятным способом решения задачи нахождения меньшего угла в треугольнике с отношением 361:1. Он позволяет визуализировать задачу и легко найти решение с помощью графических построений.