Как найти медиану треугольника по формуле mс: подробное объяснение и примеры расчета

Медиана треугольника — это линия, проходящая из вершины треугольника к серединной точке противоположной стороны. Для нахождения медианы треугольника можно использовать формулу mс, где m — середина стороны треугольника, с — противоположная этой стороне вершина. Чтобы найти медиану, нужно найти середины всех сторон треугольника и соединить их с противоположными вершинами. Медианы треугольника пересекаются в одной точке, называемой центром тяжести или барицентром. Этот метод помогает найти барицентр треугольника и определить его равновесные точки. Давайте рассмотрим подробные объяснения и примеры расчета медианы треугольника по формуле mс.

Что такое медиана треугольника?

Медианы треугольника играют важную роль в геометрии и имеют несколько интересных свойств. Во-первых, медианы равны по длине, то есть каждая из трех медиан делит сторону треугольника на две равные части. Во-вторых, точка пересечения медиан, центр масс треугольника, делит каждую медиану в отношении 2:1. Это означает, что расстояние от вершины треугольника до центра масс треугольника вдвое больше, чем расстояние от центра масс до середины противоположной стороны.

Медианы треугольника также имеют важное геометрическое свойство — они делят площадь треугольника пополам. Это означает, что если мы проведем медиану из одной вершины треугольника, она разделит площадь треугольника на две равные части.

Зная длины сторон треугольника, можно легко вычислить медианы. Для этого нужно использовать формулу медианы треугольника, которая гласит:

медиана = 0.5 * √(2 * (a^2 + b^2) — c^2)

где a, b и c — длины сторон треугольника. Применив эту формулу к каждой стороне треугольника, можно вычислить длину каждой медианы.

Например, у нас есть треугольник со сторонами a = 5, b = 7 и c = 9. Вычислим медиану относительно стороны a:

медиана = 0.5 * √(2 * (5^2 + 7^2) — 9^2)

медиана = 0.5 * √(2 * (25 + 49) — 81)

медиана = 0.5 * √(2 * 74 — 81)

медиана = 0.5 * √(148 — 81)

медиана = 0.5 * √67

медиана ≈ 2.59

Таким образом, медиана треугольника относительно стороны a равна примерно 2.59.

Итак, медиана треугольника – это отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны. Она равна по длине и делит сторону треугольника на две равные части. Медианы также пересекаются в одной точке, называемой центром масс треугольника. Эти свойства могут быть использованы для решения различных задач в геометрии.

Как найти медиану треугольника с использованием формулы mс

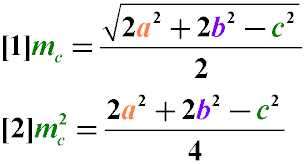
Для того чтобы найти медиану треугольника по формуле mс, нам потребуются следующие данные: координаты вершин треугольника.

Пусть координаты вершин треугольника A(x₁,y₁), B(x₂,y₂) и C(x₃,y₃).

Для нахождения медианы треугольника, проходящей через вершину C, используется следующая формула:

mс = (AC_x + BC_x) / 2, (AC_y + BC_y) / 2

где AC_x = (x₁ + x₃)/2, AC_y = (y₁ + y₃)/2 — координаты середины стороны AC,

а BC_x = (x₂ + x₃)/2, BC_y = (y₂ + y₃)/2 — координаты середины стороны BC.

Таким образом, мы находим середины сторон AC и BC путем нахождения среднего арифметического значений координат вершин этих сторон. Затем, подставляя найденные значения в формулу для медианы, находим ее координаты.

Рассмотрим пример:

Пусть вершины треугольника имеют следующие координаты: A(2, 3), B(4, 6) и C(7, 5).

Вычислим координаты середин сторон AC и BC:

AC_x = (2 + 7)/2 = 4.5, AC_y = (3 + 5)/2 = 4.

BC_x = (4 + 7)/2 = 5.5, BC_y = (6 + 5)/2 = 5.5.

Теперь подставим найденные значения в формулу медианы:

mс = (4.5 + 5.5)/2, (4 + 5.5)/2 = (10)/2, (9.5)/2 = (5, 4.75).

Таким образом, медиана треугольника, проходящая через вершину C, имеет координаты (5, 4.75).

Применение формулы mс позволяет быстро и точно находить координаты медианы треугольника. Эта формула основывается на принципе нахождения середины сторон, что делает ее простой и эффективной в использовании.

Примеры расчета медианы треугольника

Медиана треугольника mс = √((2a² + 2b² — c²)/4),

где a, b и c — длины сторон треугольника.

Давайте рассмотрим несколько примеров для лучшего понимания:

• Пример 1:

  Дан треугольник ABC с длинами сторон a = 6, b = 8 и c = 10.

  Применяя формулу:

  mс = √((2 * 6² + 2 * 8² — 10²) / 4) = √((72 + 128 — 100) / 4) = √(100 / 4) = √25 = 5

  Таким образом, медиана треугольника ABC будет равна 5.

• Пример 2:

  Дан треугольник XYZ с длинами сторон a = 4, b = 4 и c = 5.

  Применяя формулу:

  mс = √((2 * 4² + 2 * 4² — 5²) / 4) = √((32 + 32 — 25) / 4) = √(39 / 4) ≈ √9.75 ≈ 3.12

  Таким образом, медиана треугольника XYZ будет приближенно равна 3.12.

Это примеры расчета медианы треугольника с использованием формулы mс. Зная длины сторон треугольника, вы можете легко найти длину медианы и используя этот результат в различных приложениях и задачах, связанных с треугольниками.