- Определение косинуса угла
- Тригонометрический круг и его связь с косинусом
- Формула для вычисления косинуса угла в прямоугольном треугольнике
- Примеры вычислений косинуса угла
- Пример 1: Вычисление косинуса угла в прямоугольном треугольнике
- Пример 2: Вычисление косинуса угла в произвольном треугольнике
- Пример 3: Вычисление косинуса угла в треугольнике на координатной плоскости
- Пример 4: Вычисление косинуса угла при помощи тригонометрической таблицы
- Применение косинуса угла в реальной жизни
Косинус угла – это математическая функция, которая позволяет нам определить отношение прилежащего катета к гипотенузе прямоугольного треугольника. Для вычисления косинуса угла нам понадобится знать длины прилежащего катета и гипотенузы треугольника. После этого нужно разделить длину прилежащего катета на длину гипотенузы, и мы получим значение косинуса угла. Пример вычисления косинуса угла: Пусть прилежащий катет равен 3 см, а гипотенуза – 5 см. Тогда косинус угла будет равен 3/5, то есть 0,6. Таким образом, мы можем использовать косинус угла для решения различных задач, связанных с треугольниками и тригонометрией.
Определение косинуса угла
Иными словами, косинус угла равен отношению длины прилежащей стороны к гипотенузе треугольника. Эта функция обычно обозначается как cos и может принимать значения от -1 до 1. Значение косинуса угла позволяет определить, насколько сильно две стороны примыкают друг к другу.
Например, если угол α находится между сторонами a и c треугольника, то косинус угла α выражается формулой:
- cos(α) = a / c
Таким образом, зная длины сторон a и c треугольника, можно вычислить косинус интересующего нас угла α.
| Угол (градусы) | Косинус угла (cos) |
|---|---|
| 0° | 1 |
| 30° | 0,866 |
| 45° | 0,707 |
| 60° | 0,5 |
| 90° | 0 |
Таблица значений косинуса угла в градусах поможет вам быстро определить, какой косинус соответствует конкретному углу. Зная значение косинуса, можно дополнительно использовать обратную функцию, называющуюся арккосинус, чтобы найти сам угол.
Используя эти знания о косинусе угла, вы сможете легко решать различные задачи, связанные с треугольниками и измерением углов.
Тригонометрический круг и его связь с косинусом
Тригонометрический круг имеет специальные особенности, которые помогают нам вычислять значения тригонометрических функций, включая косинус. Для начала, давайте посмотрим на оси, которые проходят через центр круга. Горизонтальная ось называется осью абсцисс, а вертикальная ось — осью ординат.
Теперь, давайте представим, что наш треугольник находится внутри этого круга, с одной вершиной в точке (0,0) и одной стороной, которая является радиусом окружности. Другая сторона треугольника будет лежать на пересечении границы круга и горизонтальной оси (ось абсцисс).
Теперь, представьте себе, что вы находитесь на этой пересечении и двигаетесь по границе круга в направлении от точки (0,0) против часовой стрелки. Угол между радиусом окружности, которая соединяет точку (0,0) с вашей текущей позицией, и горизонтальной осью, называется углом синуса.
Тем не менее, нам нужно косинус, а не синус. Но не беспокойтесь, у нас есть еще одно интересное открытие: косинус угла представляет собой координату X точки на границе круга, на которой вы находитесь сейчас.
Из этого следует, что значение косинуса угла на тригонометрическом круге будет равно значению оси абсцисс в данной точке. Таким образом, если ваш угол синуса равен 30 градусам, значение косинуса этого угла будет равно 0,87.
Вот как вычислить косинус любого угла, используя тригонометрический круг! Просто найдите свой угол на круге, найдите соответствующую точку на пересечении границы круга и горизонтальной оси, и возьмите значение координаты X этой точки, чтобы получить значение косинуса.
Теперь, когда вы знакомы с тригонометрическим кругом и его связью с косинусом, вы можете смело приступить к решению задач и вычислению косинуса углов в треугольниках.
Формула для вычисления косинуса угла в прямоугольном треугольнике
Для вычисления косинуса угла в прямоугольном треугольнике используется формула:
cos(α) = a / c
- cos(α) — косинус угла α;
- a — длина стороны, прилегающей к углу α;
- c — длина гипотенузы треугольника.
Косинус угла в прямоугольном треугольнике представляет собой отношение прилегающей стороны к гипотенузе.
Давайте рассмотрим пример вычисления косинуса угла в прямоугольном треугольнике. Предположим, у нас есть прямоугольный треугольник со сторонами a = 4 и c = 5. Нам нужно найти косинус угла α.
Используя формулу для вычисления косинуса угла в прямоугольном треугольнике, подставим известные значения:
cos(α) = 4 / 5
Теперь мы можем вычислить косинус угла α:
cos(α) = 0.8
Таким образом, косинус угла α в данном примере равен 0.8. Это означает, что длина прилегающей стороны к углу α составляет 0.8 от длины гипотенузы треугольника.
Использование данной формулы позволяет легко вычислять косинус угла в прямоугольном треугольнике и применять его в различных геометрических и тригонометрических задачах.
Примеры вычислений косинуса угла
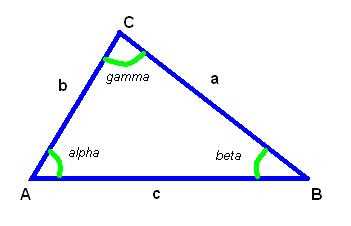
Вычисление косинуса угла может быть полезным во множестве ситуаций, от изучения геометрии до применения в физике и инженерии. Вот несколько примеров, которые помогут наглядно представить этот процесс.
Пример 1: Вычисление косинуса угла в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник со сторонами a = 3 и b = 4. Мы хотим найти косинус угла α, который является углом между горизонтальной стороной (b) и гипотенузой (c).
Мы знаем, что косинус угла определяется как отношение прилежащего катета к гипотенузе.
В данном случае, прилежащий катет равен 3, а гипотенуза равна 5 (вычисляется по теореме Пифагора: c = √(a² + b²) = √(3² + 4²) = √(9 + 16) = √25 = 5).
Таким образом, косинус угла α равен 3/5 или 0.6.
Пример 2: Вычисление косинуса угла в произвольном треугольнике
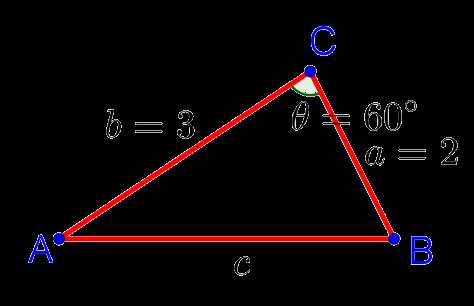
Предположим, у нас есть произвольный треугольник со сторонами a = 5, b = 7 и c = 9. Нам нужно найти косинус угла γ, который находится против стороны c.
Мы можем использовать закон косинусов, который гласит: c² = a² + b² — 2ab · cos(γ), чтобы найти косинус угла γ.
Подставим известные значения в формулу:
9² = 5² + 7² — 2 · 5 · 7 · cos(γ)
81 = 25 + 49 — 70 · cos(γ)
70 · cos(γ) = 81 — 25 — 49
70 · cos(γ) = 7
cos(γ) = 7 / 70
cos(γ) = 0.1
Таким образом, косинус угла γ равен 0.1.
Пример 3: Вычисление косинуса угла в треугольнике на координатной плоскости
Представим, что у нас есть треугольник на координатной плоскости с вершинами в точках A(2, 4), B(5, 1) и C(8, 3). Мы хотим найти косинус угла ABC, который является углом между AB и BC.
Мы можем использовать формулу косинуса, которая гласит: cos(ABC) = (AB · BC) / (|AB| · |BC|), чтобы найти косинус угла ABC.
Сначала вычислим векторы AB и BC:
AB = (5-2, 1-4) = (3, -3)
BC = (8-5, 3-1) = (3, 2)
Теперь найдем длины векторов:
|AB| = √(3² + (-3)²) = √(9 + 9) = √18 = 3√2
|BC| = √(3² + 2²) = √(9 + 4) = √13
Теперь подставим значения в формулу:
cos(ABC) = ((3, -3) · (3, 2)) / (3√2 · √13)
cos(ABC) = (3·3 + (-3)·2) / (3√2 · √13)
cos(ABC) = (9 — 6) / (3√2 · √13)
cos(ABC) = 3 / (3√2 · √13)
cos(ABC) = 1 / (√2 · √13)
cos(ABC) = 1 / (√26)
Округляя до более простой формы, косинус угла ABC равен 1 / √26.
Пример 4: Вычисление косинуса угла при помощи тригонометрической таблицы
Тригонометрическая таблица предоставляет значения косинуса углов для различных значений. Например, посмотрим на таблицу значений косинуса:
| Угол (градусы) | Косинус |
|---|---|
| 0° | 1 |
| 30° | √3/2 |
| 45° | √2/2 |
| 60° | 1/2 |
| 90° | 0 |
Для примера, предположим, что мы хотим вычислить косинус угла 45 градусов. Используя таблицу, мы можем увидеть, что значение косинуса для этого угла равно √2/2.
Таким образом, косинус угла 45 градусов равен √2/2.
Вот несколько примеров вычисления косинуса угла. Они помогут вам лучше понять, как использовать эти концепции и формулы в практическом применении. Не стесняйтесь экспериментировать с различными треугольниками и углами, чтобы углубить свое понимание и навыки в вычислении косинуса.
Применение косинуса угла в реальной жизни
Косинус угла находит широкое применение в различных областях нашей жизни, от физики и математики до инженерии и компьютерной графики. Этот математический инструмент позволяет нам анализировать и понимать различные явления и взаимодействия в окружающем нас мире.
Примером реального применения косинуса угла может служить архитектура. При проектировании зданий и конструкций необходимо учитывать нагрузки, подвергаемые различным элементам. Косинус угла помогает инженерам определить, какую силу приложить к элементу, чтобы он справился с возникающими напряжениями. Также косинус угла используется для определения наклона крыши здания, чтобы обеспечить правильное стеклоотводление и предотвратить скопление воды на поверхности.
Косинус угла также находит применение в астрономии. При наблюдении звезд и планет необходимо учитывать их положение и углы наклона. Косинус угла позволяет определить, какое количество света от звезды или планеты достигает наблюдателя, и как это может влиять на их видимую яркость.
В мире компьютерной графики косинус угла используется для создания реалистических трехмерных моделей. Он позволяет определить уровень освещения объектов в сцене, что помогает создать эффект объемности и тени. Косинусный закон также используется для расчета отраженного и преломленного света, что позволяет создавать реалистические эффекты иллюминации.
Таким образом, косинус угла играет важную роль в понимании и применении различных явлений и взаимодействий в реальной жизни. Он является мощным инструментом для анализа, моделирования и определения параметров в различных областях и науках.






