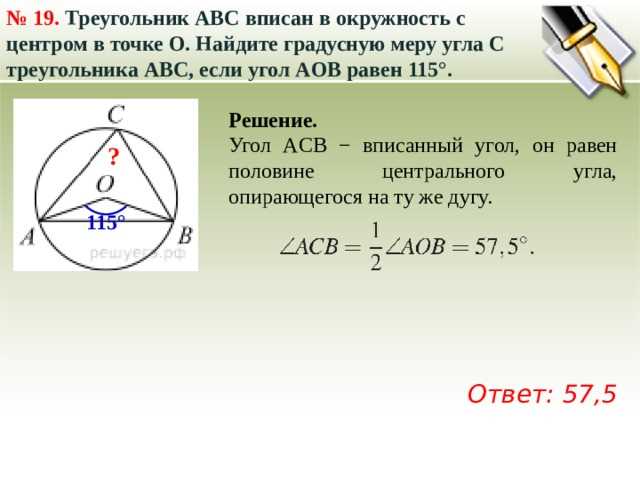
Если у вас есть окружность и вы знаете длину ее диаметра и радиус, то вы можете вычислить градусную меру угла ∠ACB, где AB — хорда окружности, а C — точка на окружности. Для этого можно использовать геометрические свойства окружности и тригонометрические функции.
Первым шагом нужно найти длину хорды AB, которая равна двойному произведению радиуса на синус половины градусного измерения угла ∠ACB. Затем найдите градусную меру этого угла, используя арксинус отношения длины хорды к длине диаметра окружности. Применяя эти формулы, вы сможете точно определить градусную меру угла ∠ACB по известным данным.
Определение градусной меры ∠ACB по длине диаметра и радиусу окружности
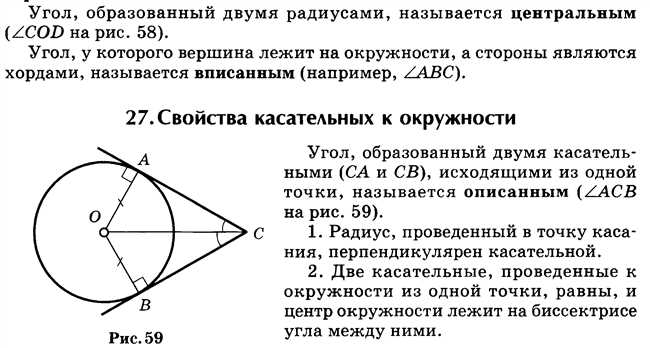
Вы хотите узнать, как определить градусную меру ∠ACB? Давайте начнем с базовых определений.
Диаметр окружности — это отрезок, проходящий через центр окружности и соединяющий две точки на самой окружности. Радиус — это половина длины диаметра и он также проходит через центр окружности.
Для нахождения градусной меры ∠ACB, мы можем использовать знания о свойствах окружностей и треугольников.
Мы знаем, что вписанный угол, охватывающий дугу на окружности, равен половине меры этой дуги. Если ∠ACB — это вписанный угол, то мы можем найти его градусную меру. Нам также известно, что треугольник ∆ACB — равнобедренный, так как AC и BC являются радиусами окружности.
Теперь, чтобы найти градусную меру ∠ACB, мы можем использовать формулу:
| Формула: | ∠ACB = 180 — 2 × ∠CBA |
Где ∠CBA — это градусная мера угла, образованного BC, радиусом окружности.
Итак, теперь, когда у нас есть радиус и диаметр окружности, мы можем подставить их в эту формулу и решить ее для нахождения градусной меры ∠ACB.
Уверены, что вам это понятно. Теперь возникли ли у вас вопросы или у вас есть что-то добавить?
Шаг 1: Понимание понятия градусной меры
В данном случае мы обсуждаем угол ∠ACB, который образуется при пересечении двух лучей, начинающихся в точке C и проходящих через точки A и B. Длина диаметра и радиуса окружности тесно связаны с градусной мерой этого угла.
Основываясь на свойствах окружностей, мы знаем, что радиус окружности равен половине диаметра. Проще говоря, диаметр — это два радиуса, а радиус — это половина диаметра. Теперь давайте посмотрим, как эти значения относятся к градусной мере угла ∠ACB.
Вы можете вообразить окружность с центром в точке C и провести радиус от точки C до точки A. Теперь давайте представим, что этот радиус перемещается по окружности до точки B. Градусная мера угла ∠ACB будет определяться тем, насколько «развернется» радиус от точки A до точки B.
Зная, что полный оборот окружности составляет 360 градусов, мы можем связать этот оборот с длиной диаметра. Дважды развернув радиус с начальной точки A до конечной точки B, мы фактически проходим полный оборот окружности, что соответствует 360 градусам.
Теперь, зная, что диаметр равен двум радиусам, и полный оборот окружности составляет 360 градусов, мы можем применить эти понятия к нашей задаче. Если длина диаметра известна, мы можем вычислить градусную меру угла ∠ACB, исходя из этих соотношений.
Шаг 2: Определение связи между диаметром и градусной мерой
Чтобы найти градусную меру ∠ACB по длине диаметра и радиусу окружности, мы должны понять, как диаметр связан с градусной мерой.
Диаметр — это отрезок, который соединяет две точки на окружности и проходит через ее центр. Он является самой длинной хордой (отрезком, соединяющим две точки на окружности), и делит окружность на две равные части, называемые половинами окружности или дугами.
Градусная мера — это значение, которое указывает, какая дуга окружности занимает определенный угол. В самом простом случае градусная мера составляет 360 градусов, что равно полной окружности. Один градус равен 1/360 части полной окружности.
Теперь давайте рассмотрим связь между диаметром и градусной мерой. Градусная мера угла, образованного диаметром, всегда составляет 180 градусов. Это может быть легко доказано с использованием свойства углов в полуокружности.
Угол ACB, образованный диаметром, является прямым углом, так как его стороны лежат на радиусах, соединяющих центр окружности с точками A и B. Из свойства угла в полуокружности следует, что градусная мера прямого угла, равного углу ACB, составляет 180 градусов.
То есть, градусная мера ∠ACB всегда равна 180 градусам, независимо от диаметра и радиуса окружности.
Шаг 3: Расчет градусной меры ∠ACB по длине диаметра и радиусу окружности
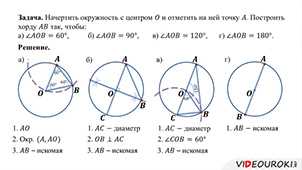
Теперь, когда у нас есть информация о длине диаметра и радиусе окружности, мы можем рассчитать градусную меру ∠ACB. Чтобы это сделать, мы воспользуемся формулой, которая связывает длину дуги окружности, радиус и градусную меру угла.
Для начала, нам необходимо понять, какая часть окружности соответствует углу ∠ACB. С помощью формулы, которая связывает длину дуги и градусную меру угла, мы можем найти эту величину. Формула выглядит следующим образом:
Длина дуги окружности = (градусная мера угла ∠ACB/360) * 2πr
где r — радиус окружности.
Мы знаем длину диаметра, и с помощью формулы для нахождения длины диаметра, мы можем выразить ее через радиус:
Длина диаметра = 2r
Отсюда мы можем найти радиус, разделив длину диаметра на 2:
Радиус = Длина диаметра / 2
Зная значение радиуса, мы можем использовать формулу для длины дуги и подставить полученные значения:
Длина дуги окружности = (градусная мера угла ∠ACB/360) * 2π * (Длина диаметра / 2)
Теперь, чтобы найти градусную меру угла ∠ACB, мы можем переставить переменные в формуле:
градусная мера угла ∠ACB = (Длина дуги окружности / (2π * (Длина диаметра / 2))) * 360
Подставляя значения диаметра и радиуса в эту формулу, мы получаем окончательное значение градусной меры угла ∠ACB.
Используя этот метод, мы можем точно рассчитать градусную меру угла ∠ACB по длине диаметра и радиусу окружности. Это очень полезный инструмент для геометрии и науки в целом.
Шаг 4: Проверка результатов расчета
После выполнения всех предыдущих шагов, мы получили значения диаметра окружности и радиуса. Теперь настало время проверить правильность наших вычислений и убедиться в полученных результатах.
Для этого нам понадобится знание формулы для вычисления градусной меры угла. По определению, градусная мера угла равна отношению длины дуги, заключенной между сторонами угла, к длине дуги полного круга.
Применяя данную формулу к нашей задаче, мы можем вычислить градусную меру ∠ACB, используя значения диаметра окружности и радиуса.
Для контроля и проверки результатов, рекомендуется использовать специализированные математические программы или онлайн-калькуляторы, которые автоматически выполнят расчеты и выдают точные значения.
Также следует отметить, что при решении данной задачи необходимо учитывать точность измерений и возможную погрешность. Поэтому, чтобы получить более точный результат, рекомендуется использовать более точные инструменты и проводить несколько независимых измерений.
В итоге, путем сравнения наших расчетов с результатами, полученными с помощью специализированных программ или калькуляторов, мы сможем убедиться в правильности наших вычислений и завершить нашу задачу.






