Как найти длину высоты равностороннего треугольника со стороной 5√3: легкий способ и формула вычисления

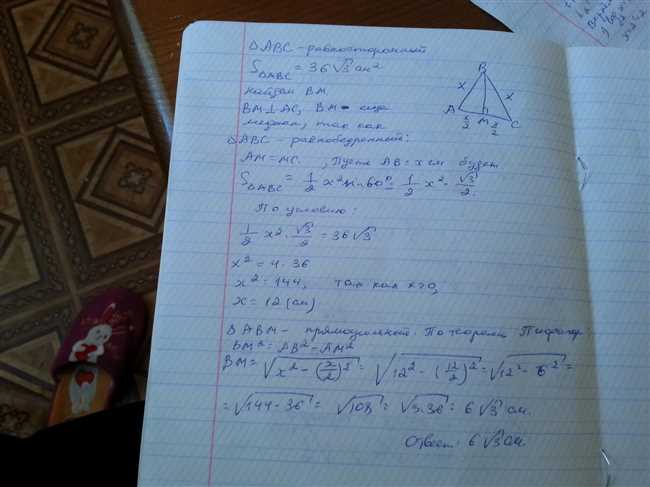
Высота равностороннего треугольника – это отрезок, проведенный из вершины перпендикулярно к противолежащей стороне.

Для нахождения длины высоты равностороннего треугольника со стороной 5√3 можно использовать теорему Пифагора и свойства равностороннего треугольника.

Также существует формула, которая позволяет найти длину высоты равностороннего треугольника по его стороне:

h = (sqrt(3) / 2) * a

Где h — высота треугольника, a — сторона треугольника.

Используя данную формулу, можно найти длину высоты равностороннего треугольника со стороной 5√3.

Определение высоты треугольника

Для вычисления высоты треугольника, важно знать длину одной из его сторон и один из углов. Например, для равностороннего треугольника высота делит его боковые стороны пополам и образует два прямых треугольника.

Если вам дано уравнение гипотетической стороны треугольника, вы можете применить различные методы для определения его высоты. Например, для прямоугольного треугольника, высота будет равна произведению длины стороны треугольника, попереченной к высоте, на синус угла между этими сторонами. В случае равнобедренного треугольника, высота будет получена путем применения теоремы Пифагора и нахождения отношения между длиной основания и половиной длины стороны.

Найдите длину высоты равностороннего треугольника со стороной 5√3 можно с помощью применения формулы, которая гласит: h = (a√3)/2, где h — высота, a — сторона треугольника. В данном случае, подставляя значения, мы получаем: h = (5√3 * √3)/2 = 5.

Равносторонний треугольник: основные свойства

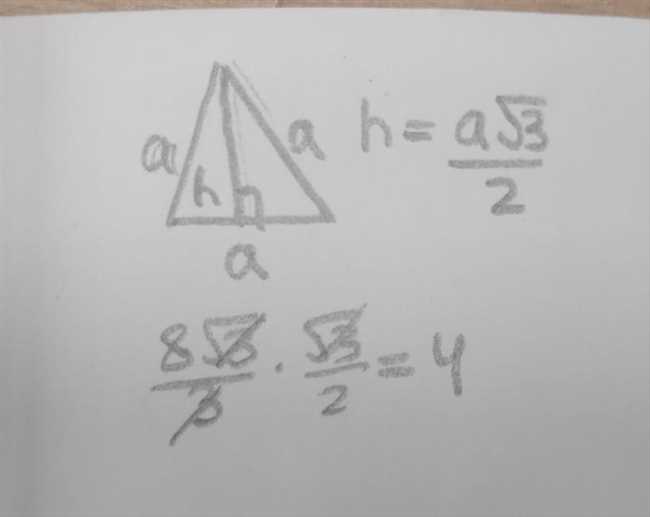
1. Углы равностороннего треугольника всегда равны 60 градусов. Это означает, что каждый угол равностороннего треугольника равен 60 градусов. Это связано с тем, что сумма углов в треугольнике равна 180 градусов, и в равностороннем треугольнике все три угла равны.

2. Высоты равностороннего треугольника пересекаются в одной точке. Если мы проведем высоты из вершин равностороннего треугольника, то они пересекутся в одной точке, называемой ортоцентром. Это свойство может быть использовано, чтобы найти высоту треугольника или его центр окружности.

3. Площадь равностороннего треугольника можно найти с помощью формулы. Площадь равностороннего треугольника можно вычислить, используя формулу: Площадь = (сторона^2 * √3) / 4. Например, для треугольника со стороной 5√3 площадь будет равна (5√3)^2 * √3 / 4.

4. Сторона равностороннего треугольника может быть найдена, зная радиус его описанной окружности. Если мы знаем радиус описанной окружности равностороннего треугольника, мы можем найти его сторону, используя формулу: Сторона = 2 * радиус * √3.

Итак, равносторонний треугольник имеет много интересных и полезных свойств. Надеюсь, теперь вы лучше понимаете, как использовать эти свойства, чтобы решать задачи и находить длину высоты или другие параметры равностороннего треугольника.

Метод нахождения длины высоты равностороннего треугольника со стороной 5√3

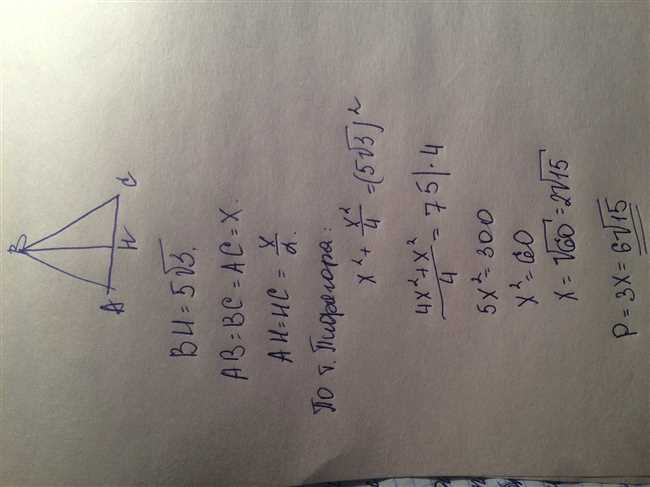
Положим, длина высоты этого треугольника равна h. Теперь, чтобы найти h, нам понадобится использовать теорему Пифагора. Но перед тем, как мы воспользуемся ею, давайте найдем значение каждой стороны треугольника, чтобы иметь полное представление о задаче.

1. Если одна сторона равностороннего треугольника равна 5√3, то все три стороны равны 5√3.
2. Высота, которую мы ищем, делит равносторонний треугольник на два равносторонних треугольника со сторонами h, h и 5√3.
3. Мы можем считать, что одно из равносторонних треугольников разбито пополам по горизонтали.

Используя теорему Пифагора в разбитом пополам два разносторонних треугольника со сторонами 5√3, 5√3 и h, мы можем записать следующее уравнение:

(5√3)² = h² + (5√3/2)²

Упростим данное уравнение, подставляя уже известные значения:

75 = h² + 45/4

Теперь, чтобы найти значение h, нам нужно решить это уравнение. Вычитая 45/4 из обеих сторон и умножая результат на 4/4, мы получим:

h² = 75 — 45/4 = 300/4 — 45/4 = 255/4

Чтобы избавиться от знаменателя 4 и найти значение h, мы возьмем квадратный корень из обеих сторон уравнения:

h = √(255/4)

Вычисляя данное уравнение, мы получим значение высоты:

h ≈ 7,01

Итак, мы нашли длину высоты равностороннего треугольника со стороной 5√3. Она составляет примерно 7,01. Теперь, когда вы знаете этот метод, вы можете легко решить подобную задачу. Удачи вам!

Пример вычисления высоты треугольника

В данной статье мы рассмотрели пример вычисления высоты равностороннего треугольника со стороной 5√3.

Для начала мы воспользовались формулой для рассчета высоты равностороннего треугольника, которая составляет:

h = a√3 / 2

Где h — высота треугольника, a — сторона треугольника.

В нашем случае, сторона равностороннего треугольника равна 5√3, поэтому мы подставили данное значение в формулу:

h = 5√3 * √3 / 2

Далее мы упростили выражение:

h = 5 * 3 / 2 = 15 / 2 = 7.5

Таким образом, длина высоты равностороннего треугольника со стороной 5√3 составляет 7.5.