Когда мы работаем с окружностями и требуется найти длину хорды, возникает вопрос: как это сделать? На самом деле, нахождение длины хорды окружности не является сложной задачей, если знать соответствующие формулы расчета. Одним из самых простых и часто используемых методов является использование теоремы о перпендикулярности хорды и радиуса. Эта теорема гласит, что те две хорды, пересекающиеся в одной точке на окружности, перпендикулярны друг к другу. С помощью этой теоремы можно найти длину хорды, зная радиус и расстояние от центра окружности до хорды. Но существует и более общая формула, которая позволяет рассчитать длину хорды по двум углам, образованным этой хордой и радиусом. В этой статье мы рассмотрим эти и другие методы расчета длины хорды окружности.
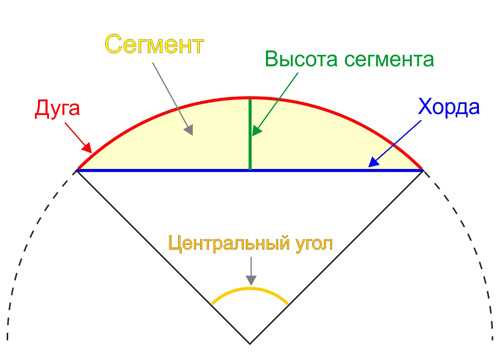
Что такое хорда окружности

Представьте себе окружность как большой круг. Теперь проведите прямую линию от одной точки окружности до другой. Вот эта линия и будет хордой. Окружность может иметь много хорд разной длины, в зависимости от расстояния между точками, которые она соединяет.
Хорда окружности является важным понятием в геометрии и находит применение в различных областях науки и техники. Например, в архитектуре могут использоваться хорды для создания арок и сводов, а в музыке — для построения аккордов на гитаре или других инструментах.
Понимание хорды окружности — это ключевой элемент в изучении геометрии, так как оно помогает в решении задач, связанных с определением расстояния между двумя точками на окружности или вычислении длины хорды.
Как найти длину хорды окружности
Для начала, что такое хорда? Хорда — это отрезок, соединяющий две точки на окружности. Хорда может быть прямой или косой, в зависимости от того, как соединены точки на окружности. Длина хорды — это расстояние между этими двумя точками.
Итак, как найти длину хорды окружности? Существует несколько методов, но наиболее простым и популярным является использование теоремы о хорде окружности.
Теорема о хорде окружности:
Если хорда пересекает другую хорду или диаметр окружности, то произведение отрезков хорды равно произведению отрезков, на которые она делит пересекаемую хорду или диаметр.
Исходя из этой теоремы, мы можем использовать следующую формулу для расчета длины хорды:
AB * CD = EF * FG
В этой формуле AB и CD представляют собой отрезки, на которые делится пересекаемая хорда, а EF и FG — отрезки, на которые делится другая хорда или диаметр.
Давайте посмотрим на пример. Предположим, у нас есть окружность с радиусом 5 см и две хорды AB и CD, которые пересекаются в точке E. Мы хотим найти длину хорды AB.
Мы знаем, что хорда CD делит диаметр окружности на две равные части — EF и FG. Пусть EF и FG будут равны по 3 см. Используя формулу, мы можем записать:
AB * 3 = 5 * 3
Решая данное уравнение, мы получим, что длина хорды AB равна 5 см.
Как видите, этот метод расчета длины хорды окружности достаточно прост и позволяет найти ответ с помощью элементарных математических операций.
Также стоит упомянуть, что существует и другой способ нахождения длины хорды окружности, используя формулу Пифагора и половину угла, опирающегося на хорду. Однако, теорема о хорде окружности является наиболее простым и быстрым методом.
Итак, кратко ответим на вопрос: как найти длину хорды окружности? Для этого используется теорема о хорде окружности. Найдите отрезки, на которые делится пересекаемая хорда, и используйте их для расчета.
Формулы для расчета длины хорды окружности
В общем случае, длину хорды окружности можно вычислить по формуле:
L = 2r sin(θ/2)
где L — длина хорды, r — радиус окружности, θ — угол, опирающийся на хорду.
Также существует формула для расчета длины хорды окружности, если известна высота, опущенная на хорду. Для этого можно воспользоваться формулой:
- Вычислить длину высоты, используя соотношение Пифагора или теорему косинусов.
- Подставить полученное значение в формулу:
L = 2√(2rh — h²)
где L — длина хорды, r — радиус окружности, h — длина высоты, опущенной на хорду.
Используя данные формулы, вы сможете легко и быстро рассчитать длину хорды окружности в различных задачах. Важно помнить, что для правильного использования формулы необходимо знать значения радиуса окружности и соответствующие углы или высоту, опущенную на хорду.
При необходимости можно также воспользоваться таблицей синусов и косинусов, чтобы получить точные значения для расчетов длины хорды окружности. Эти формулы являются полезным инструментом для работы с окружностями и могут быть применены в различных областях, где требуется расчет длины хорды окружности.






