Когда мы имеем дело с прямоугольным параллелепипедом, важно знать длину его диагонали для определения его полного размера. Диагональ является прямой линией, соединяющей две противоположные вершины параллелепипеда. Для расчета длины диагонали необходимо знать длину, ширину и высоту параллелепипеда.
Формула для расчета длины диагонали прямоугольного параллелепипеда выглядит следующим образом:
Длина диагонали = √(Длина² + Ширина² + Высота²)
После подстановки значений всех известных сторон в формулу, можно вычислить длину диагонали параллелепипеда. Такой расчет позволяет получить точный размер и легко определить пространство, которое будет занимать данный объект.
Определение понятия «прямоугольный параллелепипед»
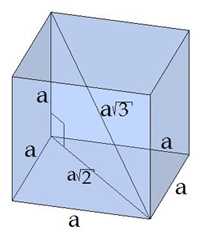
Прямоугольные параллелепипеды характеризуются тремя измерениями: длиной, шириной и высотой. Длина представляет собой расстояние между двумя противоположными гранями, ширина — расстояние между другими двумя противоположными гранями, а высота — расстояние между двумя верхней и нижней гранями.
Прямоугольные параллелепипеды имеют несколько важных свойств и характеристик. Во-первых, все углы внутри такого параллелепипеда являются прямыми. Это означает, что каждый угол равен 90 градусам. Во-вторых, диагонали, которые соединяют противоположные вершины, имеют одинаковую длину. Это свойство является основой для расчета длины диагонали прямоугольного параллелепипеда.
Прямоугольные параллелепипеды широко используются в различных областях. Например, в архитектуре они используются для создания зданий и сооружений. В технике они могут служить основой для создания различных устройств и машин. Кроме того, прямоугольные параллелепипеды могут быть использованы для упаковки и хранения товаров, поскольку их форма обеспечивает простоту транспортировки и максимизацию пространства.
Формула расчета длины диагонали прямоугольного параллелепипеда
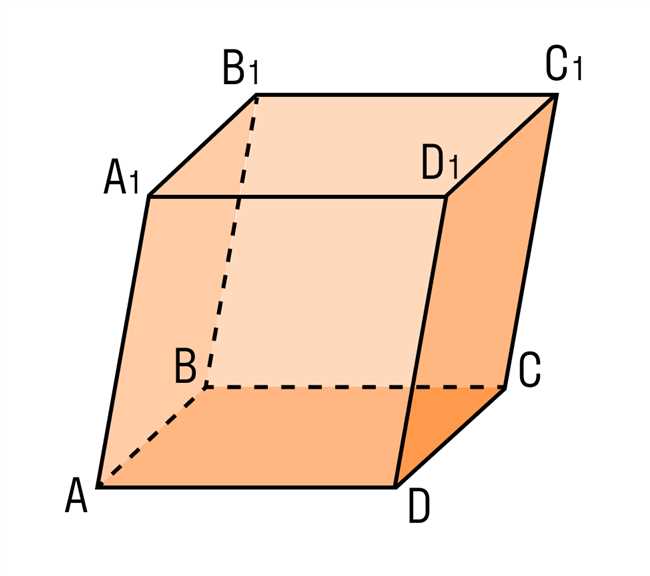
Формула расчета длины диагонали прямоугольного параллелепипеда основывается на теореме Пифагора в трехмерном пространстве. Согласно этой формуле, длина диагонали прямоугольного параллелепипеда (d) можно найти, используя длины его трех измерений — длину (a), ширину (b) и высоту (c).
Формула расчета длины диагонали прямоугольного параллелепипеда:
d = √(a^2 + b^2 + c^2)
Где:
- d — длина диагонали прямоугольного параллелепипеда;
- a — длина параллелепипеда;
- b — ширина параллелепипеда;
- c — высота параллелепипеда.
Данная формула позволит вам точно рассчитать длину диагонали прямоугольного параллелепипеда. Используя эту информацию, вы сможете решать задачи, связанные с конструкцией и геометрией, а также применять ее в повседневной жизни.
Примеры расчета
Для более наглядного понимания процесса расчета длины диагонали прямоугольного параллелепипеда, представим несколько примеров.
Пример 1: Пусть у нас есть прямоугольный параллелепипед с длиной одной из сторон (a) равной 4 см, шириной (b) равной 3 см и высотой (c) равной 5 см. Найдем длину диагонали этого параллелепипеда.
Для нахождения длины диагонали используем формулу:
диагональ = √(a^2 + b^2 + c^2)
Подставляя значения из примера, получаем:
| Сторона | Значение (см) |
|---|---|
| a | 4 |
| b | 3 |
| c | 5 |
Таким образом, подставляя значения в формулу, получаем:
диагональ = √(4^2 + 3^2 + 5^2) = √(16 + 9 + 25) = √50 ≈ 7.07 см
Таким образом, длина диагонали прямоугольного параллелепипеда равна примерно 7.07 см.
Пример 2: Рассмотрим прямоугольный параллелепипед с длиной одной из сторон (a) равной 7 м, шириной (b) равной 9 м и высотой (c) равной 12 м. Найдем длину диагонали этого параллелепипеда.
Используя ту же формулу, подставим значения:
| Сторона | Значение (м) |
|---|---|
| a | 7 |
| b | 9 |
| c | 12 |
Подставляя значения в формулу, получаем:
диагональ = √(7^2 + 9^2 + 12^2) = √(49 + 81 + 144) = √274 ≈ 16.52 м
Таким образом, длина диагонали прямоугольного параллелепипеда равна примерно 16.52 м.
Таким образом, с помощью данной формулы мы можем легко определить длину диагонали прямоугольного параллелепипеда по значениям его сторон.






