Как найти диагонали в правильном шестиугольнике: руководство и примеры

В данном руководстве мы рассмотрим, как найти диагонали в правильном шестиугольнике. Шестиугольник – это геометрическая фигура, которая имеет шесть сторон одинаковой длины и шесть углов. Диагональ – это линия, соединяющая любые две вершины фигуры, которые не являются соседними. Найдя диагонали в шестиугольнике, мы сможем определить его геометрические свойства и решать задачи связанные с этой фигурой. Для нахождения диагоналей в правильном шестиугольнике существуют специальные формулы и методы. В этом руководстве мы рассмотрим эти методы на примерах и проиллюстрируем каждый шаг.

Определение понятия «правильный шестиугольник»

• Что значит иметь «равные стороны»? Это означает, что все стороны шестиугольника имеют одинаковую длину. Независимо от выбора одной из сторон, все остальные стороны должны иметь такую же длину.
• А что значит «равные углы»? Здесь имеется в виду, что все углы внутри шестиугольника равны между собой. Угол, образованный пересечением двух сторон, также должен иметь одинаковую меру в каждом углу шестиугольника.

Вот несколько интересных фактов о правильных шестиугольниках:

1. У правильного шестиугольника все диагонали имеют одинаковую длину. Диагональ — это линия, соединяющая несмежные вершины шестиугольника.
2. Сумма всех углов внутри правильного шестиугольника равна 720 градусам. То есть, сумма углов каждого треугольника, образованного внутри шестиугольника, равна 180 градусам.
3. Правильные шестиугольники часто встречаются в мире природы. Например, медоносные пчелы строят свои соты в форме правильных шестиугольников, чтобы эффективно использовать пространство и максимизировать объем меда.

Теперь, когда вы знаете, что представляет собой правильный шестиугольник, вы можете легко определить его в геометрических фигурах и более глубоко изучить его свойства и характеристики.

Способы нахождения диагоналей в правильном шестиугольнике



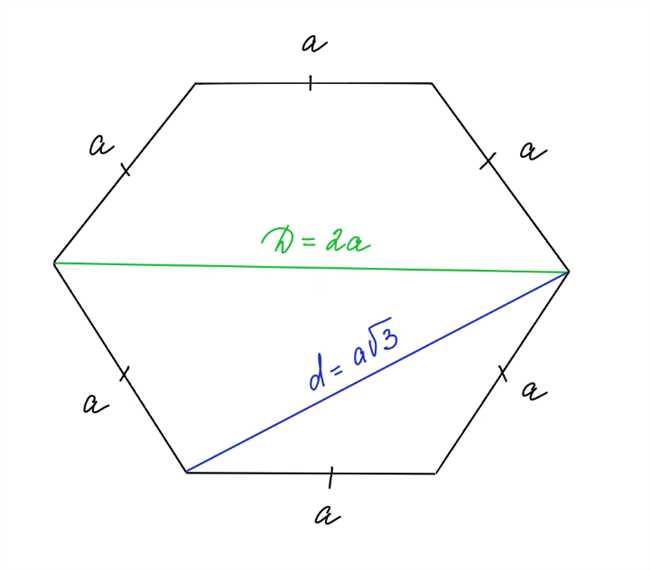
Способ 1: Угол между диагоналями

В правильном шестиугольнике каждый угол внутри фигуры равен 120 градусам. Если вы рассмотрите один из таких углов, вы увидите, что он делится на два равных угла диагональю. Это значит, что каждая диагональ делит угол на два равных угла, каждый из которых составляет 60 градусов.

Таким образом, вы можете найти угол между диагоналями в правильном шестиугольнике, зная, что он равен 60 градусам.

Способ 2: Формула для нахождения длины диагонали

Существует также формула для нахождения длины диагонали в правильном шестиугольнике. Она основана на длине стороны и угле между диагональю и стороной.

Для нахождения длины диагонали можно использовать следующую формулу:

D = 2 * S * sin(60)

Где D — длина диагонали, S — длина стороны.

Таким образом, зная длину стороны, вы можете легко вычислить длину диагонали в правильном шестиугольнике с помощью этой формулы.

Способ 3: Использование теоремы Пифагора



Также существует способ нахождения длины диагонали в правильном шестиугольнике с помощью теоремы Пифагора. Если вы знаете длины стороны и диагонали, вы можете использовать эту теорему для нахождения другой диагонали.

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Применяя эту теорему к правильному шестиугольнику, вы можете записать следующее уравнение:

D^2 = S^2 + D_2^2

Где D — длина диагонали, S — длина стороны, D_2 — длина другой диагонали.

Используя известные значения длины стороны и диагонали, вы можете решить это уравнение и найти длину другой диагонали.

Примеры нахождения диагоналей в правильном шестиугольнике

В данной статье мы рассмотрели способы нахождения диагоналей в правильном шестиугольнике. При этом мы использовали геометрический подход и формулы, основанные на свойствах фигуры.

Ниже представлены примеры вычисления диагоналей в правильном шестиугольнике:

• Пример 1: Для начала, рассчитаем длину стороны шестиугольника. Пусть сторона равна 6 см. Затем, воспользуемся формулой, которая говорит о том, что длина диагонали в правильном шестиугольнике равна двум сторонам, умноженным на синус угла в 30 градусов. Таким образом, длина диагонали будет равна 6 см * 2 * sin(30°) = 6 см * 2 * 0,5 = 6 см.
• Пример 2: Допустим, у нас есть правильный шестиугольник со стороной длиной 10 см. Для нахождения диагоналей, мы можем воспользоваться формулой: длина диагонали равна двойному произведению сторон на косинус половины угла между ними. Таким образом, длина диагонали будет равна 10 см * 2 * cos(30°) = 10 см * 2 * 0,866 = 17,32 см.

Таким образом, мы получили два примера, которые отражают способы нахождения диагоналей в правильном шестиугольнике. Мы использовали геометрические формулы и свойства фигуры, чтобы получить результаты. Надеемся, эта информация была полезной для вас!