Как найти диагональ ромба: подробная инструкция и формулы

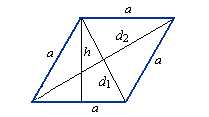
Если вы хотите рассчитать диагональ ромба, то есть несколько способов выполнить это задание. Точный ответ зависит от ваших известных данных. Но не волнуйтесь, я расскажу вам о всех доступных способах и формулах, чтобы вы могли выбрать самый подходящий для вашей ситуации.

Первый и самый простой способ — использовать формулу, основанную на длинах сторон ромба. Если вы знаете длину одной стороны и угол между ними, то можете использовать теорему косинусов для расчета диагонали.

Если у вас только известны длины сторон ромба, вы можете воспользоваться формулой, в которой используется площадь ромба и одна из сторон.

Другой способ — использовать формулу, основанную на высоте ромба. Если вы знаете высоту и одну сторону ромба, то сможете найти диагональ с помощью данной формулы.

Также существует формула, использующая данный угол и периметр ромба. Если эти данные вам известны, вы можете использовать эту формулу для расчета диагонали.

Независимо от выбранного способа, вы получите точный ответ на вопрос о диагонали ромба, используя соответствующую формулу.

Способы нахождения диагонали ромба: все формулы и методы

1. Формула для нахождения диагонали ромба по длине стороны:

Если известна длина стороны ромба, то длина его диагонали можно найти с помощью следующей формулы:

Диагональ = сторона * √2

Здесь символ √2 представляет собой квадратный корень из двух, что примерно равно 1.414

Например, если длина стороны ромба равна 6 см, то диагональ будет:

Диагональ = 6 * 1.414 = 8.48 см

2. Формула для нахождения длины диагонали ромба по площади:

Если известна площадь ромба, то длину его диагонали можно найти с помощью следующей формулы:

Диагональ = 2 * √ (Площадь / боковая сторона)

Здесь символ √ обозначает квадратный корень и деление площади на боковую сторону означает получение высоты ромба.

Например, если площадь ромба равна 24 квадратных см, а длина одной из его сторон равна 3 см, то диагональ будет:

Диагональ = 2 * √ (24 / 3) = 2 * √8 = 2 * 2.828 = 5.656 см

3. Использование теоремы Пифагора:

Если известна длина одной диагонали ромба и длина одной его стороны, то можно использовать теорему Пифагора для нахождения длины второй диагонали. Согласно этой теореме, сумма квадратов длин двух прямоугольных катетов равна квадрату гипотенузы.

Учитывая, что длины диагоналей ромба равны друг другу, можно воспользоваться этой теоремой для нахождения длины диагонали ромба по следующей формуле:

Диагональ = √ (Данная диагональ ^ 2 + Сторона ^ 2)

Например, если известно, что одна из диагоналей ромба равна 5 см, а длина его стороны равна 4 см, то вторая диагональ будет:

Диагональ = √ (5 ^ 2 + 4 ^ 2) = √ (25 + 16) = √41 ≈ 6.40 см

4. Метод измерения:

Конечно, вы всегда можете использовать измерительный инструмент, такой как линейка или мерная лента, чтобы измерить диагональ ромба. Просто расположите инструмент на диагонали и прочитайте ее длину. Этот метод является наиболее простым и надежным, но требует физической доступности ромба и измерительного инструмента.

Теперь у вас есть все необходимые формулы и методы для нахождения диагонали ромба. Вы можете выбрать подходящий способ в зависимости от ситуации и имеющихся данных. Помните, что геометрия — это весело и полезно, поэтому наслаждайтесь процессом и учитесь новому каждый день!

Формула диагонали ромба через сторону:

Для вычисления диагонали ромба, у нас есть особая формула, которая связывает длину стороны и диагонали ромба. Зная либо значение длины стороны, либо значение диагонали, мы можем легко вычислить пропущенное значение.

Формула, которую мы использовали для вычисления диагонали ромба, выражает зависимость длины стороны от диагонального отрезка и может быть записана следующим образом:

Диагональ ромба = √2 * Длина стороны

Эта формула основана на свойствах геометрии ромба и ее можно использовать для нахождения длины диагонали при известной длине стороны.

Пример:

• Длина стороны ромба: 5 см
• Диагональ ромба = √2 * (5 см) = √2 * 5 см ≈ 7.07 см

Таким образом, при известной длине стороны ромба в 5 см, длина диагонали будет примерно равняться 7.07 см.

Зная данную формулу, мы можем легко находить длину диагонали ромба, используя известные значения длины стороны.

Вы можете проверить эту формулу на практике, используя любое значение длины стороны ромба, и с уверенностью использовать ее для решения задач, связанных с нахождением диагонали ромба.

Вычисление диагонали ромба через угол наклона:

Для начала давайте вспомним, что у ромба все стороны равны между собой, а все углы равны 90 градусов. Это означает, что если у нас есть угол наклона ромба, то мы можем использовать его для вычисления диагонали.

Прежде всего, найдем одну из сторон ромба, по которой известен угол наклона. Назовем эту сторону «a». Затем мы можем использовать следующую формулу:

Диагональ ромба = a * √2

где «√2» обозначает квадратный корень из 2. Эта формула основана на том, что диагональ ромба делит его на два прямоугольных треугольника, каждый из которых имеет угол наклона в 45 градусов.

Теперь, когда у нас есть формула, давайте рассмотрим пример использования. Предположим, у нас есть ромб со стороной «a» равной 5 сантиметров, и мы хотим найти его диагональ.

Подставим значения в формулу:

1. a = 5 см

Диагональ ромба = 5 см * √2 ≈ 7.07 см

Таким образом, диагональ ромба, найденная через угол наклона, составляет около 7.07 сантиметра.

Вот и все! Теперь вы знаете, как вычислить диагональ ромба, используя его угол наклона. Надеюсь, эта информация была полезной для вас. Если у вас есть еще вопросы, не стесняйтесь задавать их.

Метод геометрической постройки для нахождения диагонали ромба:

Первый способ:

Для начала возьмите линейку и проведите две отметки на сторонах ромба так, чтобы эти отметки были на одинаковом расстоянии от вершин. Затем соедините эти отметки линейкой или карандашом. Получившаяся линия будет диагональю ромба.

Второй способ:

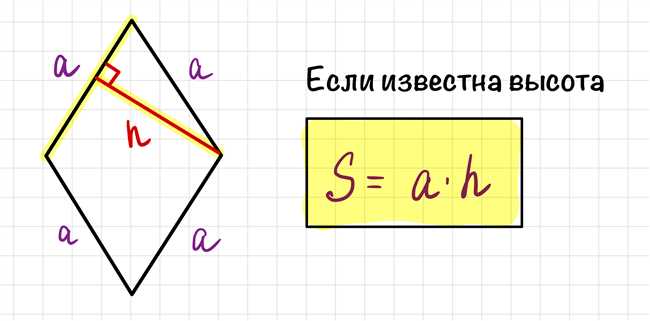
Если на плоскости уже отмечены вершины ромба, можно найти диагональ, используя рисование перпендикуляров. Для этого проведите перпендикуляры к двум противоположным сторонам ромба, проходящие через его вершины. Место пересечения этих перпендикуляров будет являться конечной точкой диагонали.

Третий способ:

Если даны только размеры сторон ромба, можно воспользоваться формулой для нахождения диагонали. Диагональ ромба можно выразить через длину его стороны с помощью следующей формулы:

Диагональ = Сторона * √2

Эта формула основана на теореме Пифагора, примененной к прямоугольному треугольнику, образуемому диагональю ромба и одной из его сторон.

Выберите тот способ, который вам наиболее удобен и поможет решить задачу нахождения диагонали ромба. Учтите, что каждый из способов может быть эффективным в зависимости от конкретной ситуации и имеющихся у вас инструментов.

Вычисление диагонали ромба через его площадь:

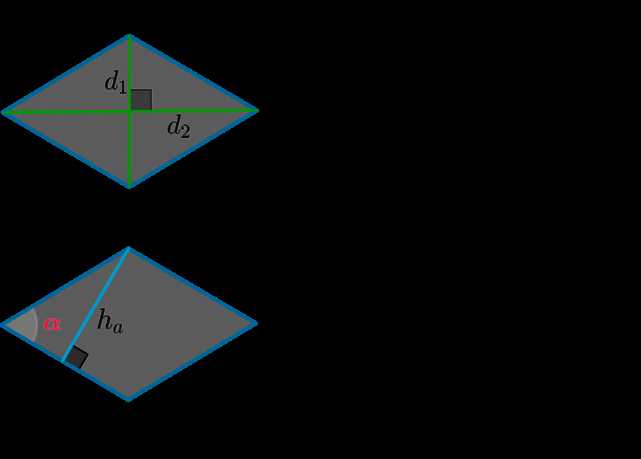
Если вам нужно найти диагональ ромба через его площадь, у вас может возникнуть несколько вопросов. Но не волнуйтесь, я помогу вам разобраться!

Диагональ ромба — это отрезок, который соединяет две противоположные вершины и пересекает их друг с другом. Чтобы найти диагональ ромба через его площадь, вам понадобятся существующие формулы и некоторые базовые знания о ромбах.

Для начала, вспомним, что площадь ромба можно найти умножением длины его диагоналей и делением полученного значения на 2:

Площадь ромба = (диагональ 1 * диагональ 2) / 2

Теперь, чтобы найти диагональ ромба, нужно переставить формулу и выразить одну из диагоналей через площадь:

Диагональ 1 = (2 * площадь ромба) / диагональ 2

Или:

Диагональ 2 = (2 * площадь ромба) / диагональ 1

Вот и все! Теперь вы знаете, как вычислить диагональ ромба через его площадь. Но не забывайте, что для использования этих формул вам нужно знать значения площади и одной из диагоналей.

Удачи в расчетах!

Формулы диагоналей ромба через радиус описанной окружности:

Для ромба с известным радиусом описанной окружности возможно вычислить длины его диагоналей с помощью следующих формул:

• Диагональ, проходящая через вершины ромба, может быть найдена по формуле:

d₁ = 2r,

где d₁ — длина диагонали, r — радиус описанной окружности.

• Длина диагонали, проходящей через середины сторон ромба, может быть вычислена по формуле:

d₂ = 2r√2,

где d₂ — длина диагонали, r — радиус описанной окружности.

Таким образом, зная радиус описанной окружности, мы можем легко вычислить длины диагоналей ромба с помощью указанных формул.