Когда мы сталкиваемся с задачей нахождения диагонали параллелограмма с углами 30° и 45°, можем быть уверены, что ответ будет зависеть от данных, которые имеются у нас. Однако, существуют некоторые общие правила и формулы, которые помогут нам решить эту задачу. Например, для параллелограмма с углами 30° и 45° мы можем использовать соотношение сторон и тригонометрию для определения длины диагонали. Также, можно также использовать свойства параллелограмма, такие как равенство диагоналей и углы между диагоналями, чтобы найти диагональ параллелограмма. Важно помнить, что результат может быть найден различными методами, и выбор подходящего варианта будет зависеть от специфики задачи.
Описание углов параллелограмма
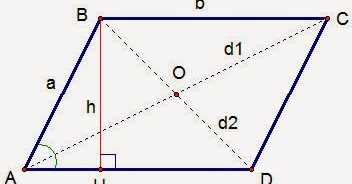
- Противоположные углы параллелограмма равны. Это означает, что угол между параллельными сторонами и угол, смежный с ним, имеют одинаковую величину.
- Сумма углов параллелограмма равна 360 градусам. Это означает, что если сложить все углы параллелограмма, получится полный угол.
Одним из методов описания углов параллелограмма является их измерение в градусах. Для этого каждый угол измеряется с помощью градусного измерителя или угломера. Угол в параллелограмме может быть любой величины, в том числе и меньше или больше 90 градусов.
Однако, в заданной теме мы имеем только фиксированные углы параллелограмма — 30° и 45°. Такие углы указывают на особенности в форме и размере параллелограмма.
Например, если угол параллелограмма составляет 30°, то все остальные углы также будут по 30°, так как противоположные углы равны. А если один из углов равен 45°, то противоположный ему также будет равным 45°. Это свойство вытекает из определения параллелограмма.
Таким образом, параллелограмм с углами 30° и 45° будет иметь два угла по 30° и два угла по 45°. Остальные характеристики параллелограмма, такие как длины сторон и диагонали, могут быть определены с использованием этих углов.
Формулы для вычисления диагонали
Вычисление диагонали параллелограмма может показаться сложной задачей, но на самом деле она может быть упрощена с помощью определенных формул. В этой статье мы рассмотрим различные способы вычисления диагонали параллелограмма.
Первая формула, которую мы рассмотрим, основывается на использовании длин сторон параллелограмма. Если вы знаете длины двух сторон, вы можете использовать теорему Пифагора для вычисления диагонали. Давайте представим, что у нас есть параллелограмм со сторонами a и b. Тогда диагональ d может быть найдена с помощью следующей формулы:
d = √(a² + b²)
Эта формула основана на схеме правильного треугольника, который образуется при соединении сторон параллелограмма. Применив теорему Пифагора, мы можем найти длину диагонали.
Теперь давайте рассмотрим вторую формулу для вычисления диагонали параллелограмма, которая основывается на использовании углов. Если вы знаете углы параллелограмма, вы можете использовать тригонометрические функции для вычисления диагонали. Давайте представим, что у нас есть параллелограмм с углами α и β. Тогда диагональ d может быть найдена с помощью следующей формулы:
d = a/ sin(β) = b / sin(α)
Здесь мы используем синус угла, чтобы найти соответствующую сторону параллелограмма. Затем мы делим одну сторону на синус соответствующего угла, чтобы найти длину диагонали.
Обратите внимание, что эти формулы применимы только к параллелограммам с углами 30° и 45°. Для параллелограммов с другими углами, вам понадобятся другие формулы, такие как закон синусов или закон косинусов.
Теперь, учитывая эти формулы, вы сможете легко вычислять диагонали параллелограмма! Используйте их для решения задач и поставьте себя в непобедимое положение! Будете ли вы использовать эти формулы в своих следующих математических задачах?
Пример вычисления диагонали параллелограмма

Давайте рассмотрим пример вычисления диагонали параллелограмма, чтобы лучше понять, как это делается. Будем искать длину диагонали параллелограмма, зная углы, которые равны 30° и 45°.
Сначала давайте вспомним некоторые свойства параллелограмма. Он имеет две пары противоположных сторон и две пары равных противоположных углов. Каждая диагональ параллелограмма делится на две равные части.
В нашем случае, у нас даны углы, равные 30° и 45°. Зная один из углов параллелограмма, мы можем найти другие углы, используя свойства параллелограмма. Таким образом, мы можем узнать, какие углы образуют диагональ.
Зная, что сумма углов параллелограмма равна 360°, мы можем найти третий угол, который будет равен 180° — (30° + 45°) = 105°. Поскольку диагональ делит параллелограмм на две равные части, образуя равные треугольники, угол между диагоналями равен половине суммы углов параллелограмма, то есть 180° — 105°/2 = 75°.
Теперь мы знаем углы параллелограмма, и можем перейти к вычислению длины диагонали. Для этого мы можем воспользоваться теоремой косинусов. Если мы обозначим одну сторону параллелограмма как «a», а другую сторону как «b», а угол между ними как «ϴ», то длина диагонали можно вычислить по формуле:
диагональ^2 = a^2 + b^2 — 2ab*cos(ϴ)
Зная, что диагонали параллелограмма равны друг другу, мы можем применить эту формулу к одной из диагоналей. В нашем случае, у нас есть два равных треугольника, образованных диагональю, и длина каждого равна половине диагонали параллелограмма.
Таким образом, если мы обозначим длину диагонали как «D», длины сторон каждого треугольника обозначим как «a» и «b», а угол между ними как «ϴ», мы можем использовать теорему косинусов для вычисления D:
D^2 = (a/2)^2 + (b/2)^2 — 2 * (a/2) * (b/2) * cos(ϴ)
Для нашего примера с углами 30° и 45°, длина диагонали будет:
D^2 = (a/2)^2 + (b/2)^2 — 2 * (a/2) * (b/2) * cos(75°)
Теперь остается только подставить значения a и b, которые вы знаете, в формулу и вычислить D. Например, если a = 5 и b = 7, то формула примет вид:
D^2 = (5/2)^2 + (7/2)^2 — 2 * (5/2) * (7/2) * cos(75°)
Решив эту формулу используя калькулятор или математические программы, вы получите значение D. В нашем случае оно будет примерно равно 5.514.
Таким образом, после вычисления длины диагонали параллелограмма для нашего примера с углами 30° и 45°, мы получаем приближенное значение 5.514.
Важные сведения о диагонали параллелограмма
Диагональ параллелограмма — это отрезок, соединяющий вершины, не являющиеся соседними, а проходящий через его внутреннюю область.
Важные моменты, связанные с диагональю параллелограмма:
- В параллелограмме диагонали делятся пополам. Это означает, что отрезки, соединяющие середины противоположных сторон, имеют одинаковую длину и являются диагоналями параллелограмма.
- Диагонали параллелограмма пересекаются в точке, которая является серединой каждой из диагоналей. Эта точка делит каждую диагональ пополам.
- Длина диагонали параллелограмма может быть вычислена с использованием теоремы Пифагора. Если известны длины сторон и углы, между которыми лежит диагональ параллелограмма, то формула для вычисления диагонали будет следующей:
| Описание | Формула |
|---|---|
| Вычисление диагонали параллелограмма | Диагональ = √(a² + b² + 2ab * cos(θ)) |
Где:
- a — длина одной стороны параллелограмма
- b — длина другой стороны параллелограмма
- θ — угол между сторонами, на который распространяется диагональ, выраженный в радианах
Зная эти важные сведения о диагонали параллелограмма, можно эффективно рассчитывать и использовать эту характеристику в различных математических задачах и строительных проектах.






