- Формула и способы
- 1. Формула
- 2. Геометрический метод
- 3. Теорема Пифагора
- Геометрическое определение диагонали куба
- Вычисление диагонали куба по известным параметрам
- Использование теоремы Пифагора для нахождения диагонали куба
- Примеры вычисления диагонали куба
- Пример 1:
- Пример 2:
- Практическое применение формулы нахождения диагонали куба
- Расчет пространства
- Дизайн и архитектура
- Создание мебели
- Различные науки
- Как найти диагональ куба
- Рекомендации по проверке правильности вычислений
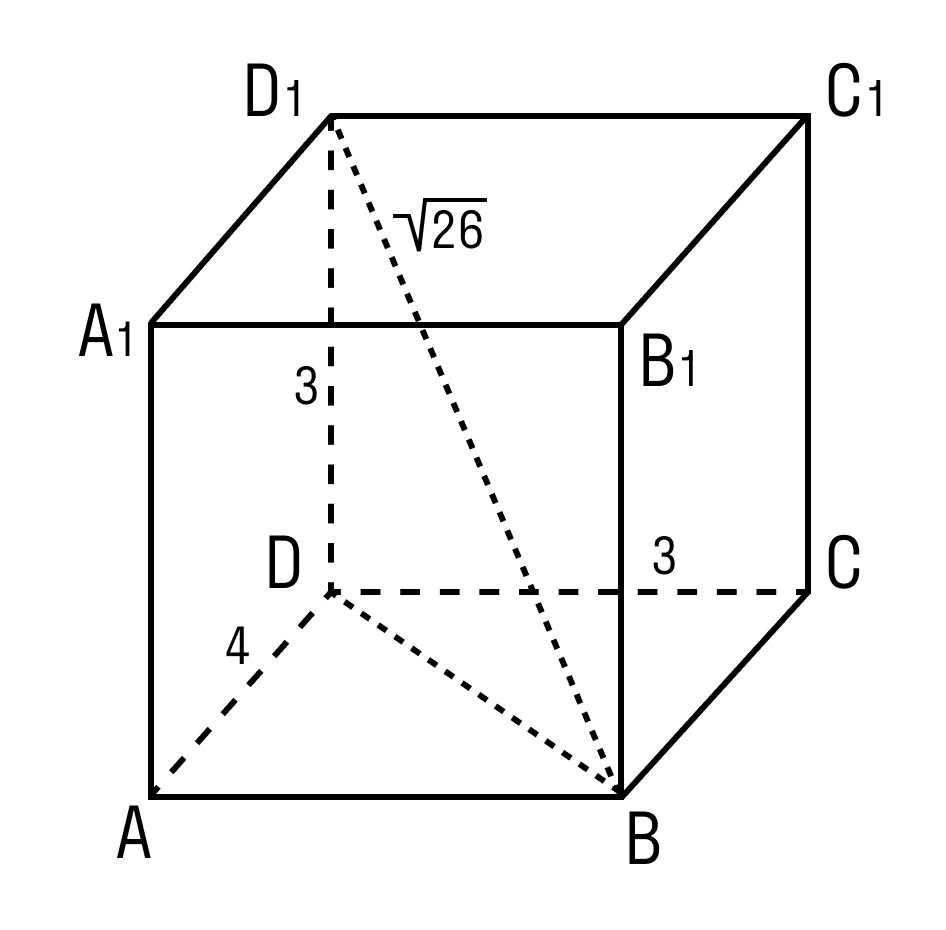
Вы когда-нибудь задумывались о том, как вычислить диагональ куба? Это может показаться сложной задачей, но на самом деле существуют простые способы и формулы для нахождения длины диагонали куба.
Одним из самых распространенных способов вычислить диагональ куба является использование формулы, основанной на теореме Пифагора. Согласно этой формуле, диагональ куба равна квадратному корню из суммы квадратов его сторон. Это означает, что если известна длина одной стороны куба, можно легко найти длину его диагонали.
Есть и другие способы найти диагональ куба. Один из них — использование теоремы Фалеса. В этом методе необходимо построить треугольник, соединяя диагональ куба с двумя его углами. Затем, используя соотношение сторон треугольника, можно вычислить длину диагонали.
Теперь, когда вы знаете о разных способах и формулах для нахождения диагонали куба, вы можете легко решить подобную задачу и узнать длину диагонали вашего куба. Не бойтесь экспериментировать и использовать эти знания в практических задачах.
Формула и способы
Существует несколько способов для нахождения диагонали куба. Рассмотрим несколько из них.
1. Формула
Самым простым и точным способом для нахождения диагонали куба является использование специальной формулы. Формула для нахождения диагонали куба выглядит следующим образом:
Диагональ куба = √3 × a
Где «a» является длиной стороны куба. Применение этой формулы позволяет найти диагональ куба с высокой степенью точности.
2. Геометрический метод
Если у вас есть физический куб, вы можете использовать геометрический метод для определения длины его диагонали. Просто соедините две противоположные вершины куба линией и измерьте получившуюся линию с помощью линейки или мерного инструмента. Этот способ достаточно прост и доступен, но может быть не так точным, как использование формулы.
3. Теорема Пифагора
Также можно использовать теорему Пифагора для нахождения длины диагонали куба. Для этого нужно знать длину стороны куба. Используя формулу теоремы Пифагора, можно вычислить длину диагонали куба:
Диагональ куба = √(a^2 + a^2 + a^2)
Где «a» — длина стороны куба. Этот метод несколько сложнее формулы, но может быть полезным для тех, кто интересуется математикой или хочет углубиться в геометрию.
Таким образом, нахождение диагонали куба может быть осуществлено с помощью формулы, геометрического метода или теоремы Пифагора. Каждый из этих способов имеет свои преимущества и может быть использован в различных ситуациях. Выберите тот, который лучше всего подходит вам и откройте для себя мир математики и геометрии!
Геометрическое определение диагонали куба
Для того чтобы понять геометрическое определение диагонали куба, давайте представим себе трехмерную модель куба, которая имеет длину, ширину и высоту. Когда мы говорим о диагонали куба, мы имеем в виду линию, которая проходит через центр куба и соединяет два противоположных угла куба.
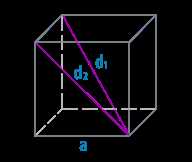
Другими словами, диагональ куба — это линия, которая идет из одного угла куба к противоположному углу, проходя через центр куба. Она имеет форму прямой линии, и ее длина равна корню квадратному из суммы квадратов длины, ширины и высоты куба.
Давайте представим, что у нас есть куб со стороной a. Чтобы найти длину диагонали куба, мы можем использовать формулу:
Длина диагонали = a * √3
То есть, длина диагонали куба равна стороне куба, умноженной на корень квадратный из 3.
Конечно, куб имеет шесть боковых граней, поэтому у него есть шесть диагоналей. Все эти диагонали одинаковы по длине и имеют общую формулу для вычисления их длины.
Зная геометрическое определение диагонали куба, мы можем легко вычислить ее длину и использовать эту информацию в различных задачах. Например, если мы хотим найти расстояние между двумя противоположными углами куба, мы можем использовать формулу для нахождения длины диагонали.
Так что теперь, когда мы знаем геометрическое определение диагонали куба, давайте посмотрим, как мы можем использовать это знание в нашей повседневной жизни!
Вычисление диагонали куба по известным параметрам
Давайте разберемся, как вычислить диагональ куба по известным параметрам. Это может быть полезно, например, при планировании строительства или при решении геометрических задач. Зная параметры куба, мы можем найти его диагональ, что позволит нам получить полное представление о его геометрических свойствах. Погрузимся в мир математики и начнем исследование!
Первое, что важно уяснить, это сам блюминг максимальное движение по диагонали куба. Диагональ — это линия, соединяющая две противоположные вершины куба и являющаяся его наибольшей диагональю.
Теперь давайте выведем формулу для вычисления диагонали куба:
Диагональ куба равна произведению длины его ребра на квадратный корень из трех:
Диагональ = ребро × √3
Также, для нахождения диагонали куба можно воспользоваться теоремой Пифагора. Согласно этой теореме, квадрат длины диагонали куба равен сумме квадратов его ребра:
Диагональ² = ребро² + ребро² + ребро²
Тогда, чтобы найти диагональ, нужно извлечь квадратный корень из правой части уравнения:
Диагональ = √(ребро² + ребро² + ребро²)
Итак, у нас есть два способа вычисления диагонали куба. Какой из них выбрать — зависит от ваших предпочтений и понимания математических принципов.
Теперь, когда вы знаете формулу, давайте рассмотрим пример:
| Параметры куба | Ребро | Диагональ |
|---|---|---|
| 1 | √(1²+1²+1²) | |
| 2 | √(2²+2²+2²) | |
| 3 | √(3²+3²+3²) |
Таким образом, если у нас есть куб со стороной длиной 1, то его диагональ будет равна √3. Если же сторона куба равна 2, то его диагональ будет равна 2√3. Аналогично, если сторона равна 3, то диагональ будет равна 3√3.
Итак, вы теперь знаете, как вычислить диагональ куба по известным параметрам. Надеюсь, этот математический путеводитель поможет вам в решении геометрических задач и будет полезен в вашей повседневной жизни!
Использование теоремы Пифагора для нахождения диагонали куба
Теорема Пифагора знакома многим из школьного курса геометрии. Она утверждает, что в прямоугольном треугольнике, квадрат длины гипотенузы (наибольшей стороны) равен сумме квадратов длин катетов (двух оставшихся сторон).
Перенесем это знание на куб. Куб имеет 6 граней, каждая из которых является квадратом. Для нахождения диагонали куба, нам нужно найти длину гипотенузы прямоугольного треугольника, образованного двумя смежными гранями куба.
Допустим, каждая сторона куба имеет длину a. Тогда, поскольку у нас есть две смежные стороны, образующие прямой угол, мы можем применить теорему Пифагора:
{$a}^2 + {$a}^2 = c^2;
где a — длина стороны куба, а c — длина диагонали. При этом мы знаем, что каждая сторона куба одинакова, поэтому мы можем упростить уравнение:
2{$a}^2 = c^2
Теперь мы можем найти диагональ куба, применяя следующую формулу:
c = √(2{$a}^2)
Для удобства вычислений мы также можем использовать алгоритмы или калькуляторы для нахождения квадратных корней и решения уравнений. Это поможет нам быстро и точно найти длину диагонали куба.
Таким образом, использование теоремы Пифагора позволяет нам находить диагональ куба, основываясь на известной длине его сторон. Это простой и эффективный метод, который может быть использован в математических и геометрических расчетах. Надеюсь, эта информация была полезной для вас!
Примеры вычисления диагонали куба
Давайте разберемся, как вычислить диагональ куба. Это необходимо знать, когда нужно найти расстояние между двумя противоположными вершинами куба или, например, если хотите узнать, какую длину проволоки нужно использовать, чтобы обернуть куб.
Для вычисления диагонали куба нужно знать любую известную сторону куба. Диагональ можно вычислить по формуле:
Диагональ куба = √(3 * a²)
Где a — сторона куба.
Давайте рассмотрим несколько примеров вычисления диагонали куба.
Пример 1:
У нас есть куб со стороной равной 5 сантиметров. Найдем длину его диагонали. Подставим значение стороны a = 5 в формулу:
Диагональ куба = √(3 * 5²)
Диагональ куба = √(3 * 25)
Диагональ куба = √75
Диагональ куба ≈ 8.66 сантиметра (округляем до двух знаков после запятой)
Пример 2:
Представьте себе куб, у которого известна длина диагонали, а нужно найти длину его стороны. Допустим, длина диагонали равна 12 сантиметров. Используя формулу для диагонали куба, выразим сторону куба:
12 = √(3 * a²)
12² = 3 * a²
144 = 3 * a²
48 = a²
a ≈ √48
a ≈ 6.93 сантиметра (округляем до двух знаков после запятой)
Таким образом, длина стороны куба равна приблизительно 6.93 сантиметра.
Теперь, когда вы знаете как использовать формулу для вычисления диагонали куба, вы можете легко решать подобные задачи. Удачи в вашем математическом путешествии!
Практическое применение формулы нахождения диагонали куба
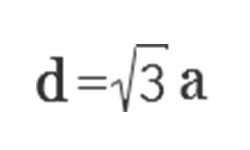
Вы уже могли заметить, что формула для вычисления диагонали куба может показаться абстрактной и теоретической. Однако, на самом деле, она может быть очень полезной в реальной жизни. В этой статье мы поговорим о практическом применении этой формулы и как она может помочь вам в различных ситуациях.
Расчет пространства
Одним из основных применений формулы для нахождения диагонали куба является расчет пространства. К примеру, представьте, что вам нужно разместить кубический объект внутри другого пространства, например, шкафа или коробки. Зная диагональ куба, вы можете убедиться, что объект будет подходить по размерам и не будет выходить за пределы доступного пространства. Это позволит вам планировать и организовывать свое пространство более эффективно и удобно.
Дизайн и архитектура
Формула нахождения диагонали куба также может быть полезной в области дизайна и архитектуры. Например, если вы проектируете комнату или дом, зная диагональ куба, вы можете легко определить, сколько объектов вы сможете разместить внутри этого пространства. Еще одно практическое применение — это расчет строительных материалов. Зная диагональ куба, вы можете определить, сколько квадратных метров плитки или обоев вам понадобится для отделки комнаты. Это поможет вам точно определить бюджет и избежать лишних затрат.
Создание мебели
Еще одно практическое применение формулы для нахождения диагонали куба — создание мебели. Зная длину диагонали куба, вы можете точно определить размеры для стола, шкафа или стеллажа. Это позволит вам изготовить мебель, которая идеально впишется в интерьер и будет максимально удобной для использования.
Различные науки
Формула для нахождения диагонали куба также широко используется в различных областях науки, таких как геометрия, физика и инженерия. Она может быть полезна при решении различных задач и проведении экспериментов. Например, в физике она может использоваться для расчета объема или давления внутри кубических контейнеров. В инженерии она может быть полезна при проектировании и строительстве различных конструкций.
Как найти диагональ куба
Теперь, когда вы понимаете практическое применение формулы, давайте быстро вспомним, как найти диагональ куба. Формула для этого выглядит следующим образом:
Диагональ = √(3 * a²)
Где «a» — это длина стороны куба. Просто возьмите длину стороны и подставьте ее в формулу, чтобы найти диагональ.
Надеюсь, эта информация была полезной для вас! Теперь вы знаете, как применить формулу для нахождения диагонали куба в реальной жизни. Используйте ее с умом, чтобы сделать свою жизнь более организованной и комфортной! Если у вас есть еще вопросы или вы хотите поделиться своим опытом, буду рад услышать ваши мысли. Хорошего дня и удачи во всех ваших предприятиях!
Рекомендации по проверке правильности вычислений
После того, как вы используете формулу для вычисления диагонали куба, рекомендуется провести проверку правильности полученного значения. Это позволит вам быть уверенным в достоверности результатов и избежать возможных ошибок.
Для проверки верности вычислений рекомендуется выполнить следующие действия:
- Проверьте корректность исходных данных: убедитесь, что значения, которые вы использовали в формуле, являются правильными и точными. Это включает проверку длин сторон куба, а также применяемых единиц измерения.
- Проверьте правильность применения формулы: удостоверьтесь, что вы правильно применили формулу для вычисления диагонали куба. Проверьте порядок операций и внимательно проследите, чтобы не допустить ошибок в вычислениях.
- Сравните полученный результат с ожидаемым: посчитайте диагональ куба, используя другие способы или проверенные источники данных. Сравните полученные значения и удостоверьтесь, что они совпадают или близки друг к другу.
- Проверьте путем измерения: в случае, если у вас есть физический куб, используйте инструменты для измерения диагонали и сравните результат с вашими вычислениями. Это поможет вам обнаружить любые расхождения или ошибки.
Правильная проверка и контроль вычислений позволят вам быть уверенным в правильности вашего результата. В случае обнаружения ошибок, вы сможете проанализировать их и исправить, чтобы получить точные и достоверные результаты.






