
Интерполяция — это метод приближенного нахождения промежуточных значений между известными точками. В контексте нахождения числа, интерполяция позволяет найти конкретное значение, основываясь на известных данных.
Один из способов применения интерполяции для нахождения числа — это использование линейной интерполяции. Она основана на представлении графика данных в виде прямой линии. Для использования этого метода необходимо иметь минимум две конечные точки и знать значения функции в этих точках.
Метод интерполяции позволяет получить более точные результаты, чем простое приближение. Он широко используется в науке, технике и экономике для анализа данных и предсказания значений. Используйте этот простой руководство, чтобы научиться применять интерполяцию для нахождения числа точнее.
Начало работы
Добро пожаловать в наше простое руководство по использованию метода интерполяции для поиска числа! Если вы часто сталкиваетесь с поиском нужного числа в большом наборе данных, то этот метод поможет вам экономить время и силы. Как мы знаем, мир диктует нам свои правила, и время становится всё более ценным ресурсом. Поэтому навык быстрого нахождения чисел может оказаться очень полезным как в работе, так и в повседневной жизни.
Представим, что у вас есть множество чисел, включая те, которые вам необходимо найти. Метод интерполяции поможет сократить количество шагов для нахождения нужного числа, значительно экономя ваше время и энергию. Некоторые люди могут быть не знакомы с этим методом или считать его сложным, но на самом деле он достаточно прост в использовании.
Основные принципы интерполяции
Основные принципы интерполяции включают:
- Выбор метода интерполяции: Существуют различные методы интерполяции, такие как линейная интерполяция, интерполяция Лагранжа, интерполяция Ньютона и сплайны. Каждый метод имеет свои преимущества и недостатки, и выбор метода зависит от точности, эффективности и требований конкретной задачи.
- Выбор узлов: Узлы — это известные значения данных, на основе которых происходит интерполяция. Их выбор может существенно влиять на точность интерполяции. Часто узлы выбираются равномерно, но также возможно использование узлов с переменным шагом или специальным распределением.
- Вычисление интерполяционного полинома: Интерполяционный полином — это аналитическая функция, определенная на основе выбранных узлов и известных значений. Его можно использовать для нахождения неизвестных значений между узлами. Вычисление полинома обычно сводится к решению системы линейных уравнений или использованию специальных формул (например, формула Лагранжа или формула Ньютона).
- Проверка точности: После нахождения интерполяционного полинома важно проверить его точность и сопоставить его с известными данными. Для этого можно использовать различные критерии, такие как сравнение значений внутри исходного набора данных или сравнение с дополнительными измерениями или моделями.
Интерполяция может быть очень полезной, когда у нас есть лишь ограниченный набор данных или когда требуется предсказать значения внутри этого набора. Она позволяет нам заполнить пробелы между точками и получить более гладкую и непрерывную функцию. Кроме того, интерполяция может быть основой для аппроксимации, экстраполяции и прогнозирования.
Таким образом, основные принципы интерполяции включают выбор метода интерполяции, выбор узлов, вычисление интерполяционного полинома и проверку точности результата. Метод интерполяции следует выбирать исходя из требований конкретной задачи, а точность вычислений следует проверять и сравнивать с известными данными.
Шаги метода интерполяции
1. Понять задачу
В первую очередь, вы должны ясно представлять, какую задачу вы пытаетесь решить. Убедитесь, что вы понимаете, какие данные у вас есть и какую информацию вы хотите получить. Также важно знать, что функция, которую вы пытаетесь интерполировать, является гладкой и непрерывной.
2. Определить известные точки
После того, как вы поняли задачу, вам нужно определить известные точки функции. Это могут быть точки, в которых вы имеете значения функции или точки, в которых вы знаете производные функции. Известные точки помогут вам создать математическую модель для интерполяции.
3. Выбрать метод интерполяции
Существует несколько методов интерполяции, и каждый из них имеет свои преимущества и ограничения. Некоторые из наиболее распространенных методов включают полиномиальную интерполяцию, интерполяцию сплайнами и метод наименьших квадратов. Выберите метод, который наилучшим образом соответствует вашим требованиям и возможностям.
4. Построить интерполяционную функцию
На основе известных точек и выбранного метода интерполяции вы можете построить интерполяционную функцию. Это будет функция, которая приближает значения неизвестной функции между известными точками. Используя эту функцию, вы сможете получить значения в промежуточных точках.
5. Вычислить значение функции
Когда интерполяционная функция построена, вы можете использовать ее для вычисления значений функции в нужных вам точках. Подставьте значения независимой переменной в интерполяционную функцию и получите соответствующие значения зависимой переменной.
6. Проверить результаты
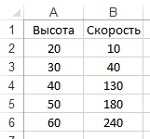
Последний шаг – проверить результаты интерполяции, особенно если у вас есть возможность сравнить их с известными значениями функции. Обязательно проверьте, насколько близки полученные значения к ожидаемым или реальным значениям. Если необходимо, можно провести дополнительные расчеты или использовать другой метод интерполяции, чтобы улучшить полученные результаты.
Надеюсь, эти шаги помогут вам применить метод интерполяции и найти нужное число. Удачи в ваших математических исследованиях!
Пример использования метода интерполяции
Метод интерполяции широко применяется в различных областях, где требуется нахождение неизвестного значения между уже известными точками. Например, в геофизике, экономике, физике, гидрологии и других науках, метод интерполяции может быть полезным инструментом для анализа данных и прогнозирования.
Рассмотрим пример использования метода интерполяции в физике. Предположим, у нас есть экспериментальные данные о зависимости температуры от времени в некоторой физической системе. При анализе этих данных нам может понадобиться найти температуру в промежуточные моменты времени, которые не были измерены.
Для этого мы можем использовать метод интерполяции, который позволит нам оценить значения температуры в нужные нам моменты времени. Например, если мы имеем известные значения температуры в моменты времени 0, 2, 4 и 6 секунд, мы можем использовать метод интерполяции для предсказания температуры в момент 3 секунды.
Применение метода интерполяции позволяет нам получить более точные и полезные результаты, чем простое экстраполирование или использование среднего значения. Это отличный инструмент для обработки данных и анализа зависимостей в различных научных и экономических исследованиях.






