- Методы и примеры поиска четвертой стороны четырехугольника
- Метод 1: Использование теоремы Пифагора
- Метод 2: Использование теоремы косинусов
- Примеры
- Геометрический метод
- Пример геометрического метода:
- Известные стороны и углы
- Метод 1: Теорема косинусов
- Метод 2: Задача на синусоиду
- Метод 3: Площадь четырехугольника
- Пример
- Поиск дополнительных углов и сторон
- 1. Метод синусов и косинусов
- 2. Теорема косинусов
- 3. Уравнения углов
- 4. Таблица углов и сторон
- Поиск с использованием теоремы Пифагора
- Применение формулы косинусов
- Использование формулы Герона
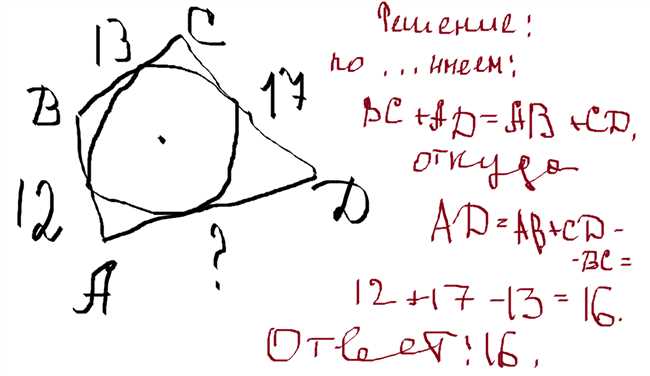
Когда мы имеем дело с четырёхугольником, знание его сторон может быть крайне полезным, особенно при решении геометрических задач. Однако, иногда нам может понадобиться найти четвёртую сторону, зная остальные три.
Существует несколько методов нахождения четвёртой стороны четырёхугольника в зависимости от известных данных. Один из таких методов — использование формулы для нахождения периметра четырёхугольника. Другой метод — использование теоремы Пифагора и знания о расстоянии между вершинами.
На практике можно применить эти методы, решая различные задачи. Например, если известны длины трёх сторон параллелограмма, можно легко вычислить четвёртую сторону, применяя указанные методы.
В данной статье мы рассмотрим подробнее эти методы и приведем несколько практических примеров из повседневной геометрии.
Методы и примеры поиска четвертой стороны четырехугольника
Метод 1: Использование теоремы Пифагора
Если угол между двумя известными сторонами четырехугольника прямой (90 градусов), мы можем использовать теорему Пифагора для вычисления длины четвертой стороны. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Поэтому, если известны длины двух сторон и угол между ними равен 90 градусов, можно воспользоваться теоремой Пифагора для вычисления длины четвертой стороны. Например, если стороны AB и BC известны, а угол ABC равен 90 градусов, то длина четвертой стороны AC может быть вычислена следующим образом:
AC = √(AB^2 + BC^2)
Метод 2: Использование теоремы косинусов
Если угол между двумя известными сторонами четырехугольника не является прямым (не равен 90 градусам), мы можем использовать теорему косинусов для вычисления длины четвертой стороны. Теорема косинусов утверждает, что квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
Поэтому, если известны длины двух сторон и угол между ними, можно воспользоваться теоремой косинусов для вычисления длины четвертой стороны. Например, если стороны AB и BC известны, а угол ABC не равен 90 градусам, то длина четвертой стороны AC может быть вычислена следующим образом:
AC = √(AB^2 + BC^2 — 2 * AB * BC * cos(ABC))
Примеры
Давайте рассмотрим несколько примеров, чтобы проиллюстрировать применение этих методов:
- Пример 1: Известны стороны AB = 3 и BC = 4, а угол ABC = 90 градусов. Какова длина четвертой стороны AC?
- Пример 2: Известны стороны AB = 5 и BC = 7, а угол ABC = 45 градусов. Какова длина четвертой стороны AC?
Мы можем использовать теорему Пифагора для вычисления длины четвертой стороны AC:
AC = √(3^2 + 4^2)
AC = √(9 + 16)
AC = √25 = 5
Мы можем использовать теорему косинусов для вычисления длины четвертой стороны AC:
AC = √(5^2 + 7^2 — 2 * 5 * 7 * cos(45))
AC = √(25 + 49 — 70 * 0.7071)
AC = √(25 + 49 — 49.4975)
AC = √24.5025 = 4.95
Таким образом, методы использования теоремы Пифагора и теоремы косинусов позволяют найти длину четвертой стороны четырехугольника, когда известны длины трех других сторон и угол между ними. Используйте эти методы, чтобы справиться с задачами поиска четвертой стороны и оттачивать свои геометрические навыки!
Геометрический метод
Для использования геометрического метода необходимо знание основных свойств четырехугольника. Например, заметим, что сумма внутренних углов четырехугольника всегда равна 360 градусов. Это свойство может быть использовано для нахождения неизвестных углов, если известны значения остальных углов.
Кроме того, можно использовать теорему Пифагора и теорему косинусов для вычисления сторон четырехугольника, если известны другие стороны и углы фигуры.
Пример геометрического метода:
Рассмотрим пример четырехугольника ABCD, в котором известны значения сторон AB, BC и CD, а также угол D. Найдем четвертую сторону AD.
- По теореме косинусов, в треугольнике BCD можно найти угол CBD и сторону BD:
- Угол CBD = arccos((BC^2 + CD^2 — BD^2) / (2 * BC * CD))
- BD = sqrt(BC^2 + CD^2 — 2 * BC * CD * cos(angle CBD))
- Затем, используя теорему косинусов, в треугольнике ABD можно найти сторону AD:
- AD = sqrt(AB^2 + BD^2 — 2 * AB * BD * cos(angle ABD))
Итак, применив геометрический метод, мы можем найти значение четвертой стороны AD в четырехугольнике ABCD, зная значения других сторон и углов фигуры.
Известные стороны и углы
Когда мы знаем все стороны и углы четырехугольника, мы можем использовать различные методы и формулы, чтобы найти четвертую сторону. Здесь я расскажу вам о нескольких из них.
Метод 1: Теорема косинусов
Если известны длины всех сторон четырехугольника и угол между двумя из них, мы можем использовать теорему косинусов для вычисления длины четвертой стороны. Формула выглядит следующим образом:
c^2 = a^2 + b^2 — 2ab*cos(C)
Где c — длина четвертой стороны, a и b — длины известных сторон, C — угол между ними.
Метод 2: Задача на синусоиду
Если известны длины двух сторон четырехугольника и угол между ними, а также диагональ, проходящая через этот угол, мы можем использовать задачу на синусоиду для вычисления длины четвертой стороны. Формула выглядит следующим образом:
c/sin(C) = d/sin(D)
Где c — длина четвертой стороны, d — длина диагонали, C — угол между известными сторонами, D — угол между диагональю и известной стороной.
Метод 3: Площадь четырехугольника
Если известны длины трех сторон четырехугольника и углы между ними, а также площадь четырехугольника, мы можем использовать формулу для вычисления длины четвертой стороны. Формула выглядит следующим образом:
a + b + c + d = 2*(sqrt(S1*S2 + S3*S4))
Где a, b, c, d — длины сторон четырехугольника, S1, S2, S3, S4 — площади треугольников, образованных сторонами четырехугольника.
Пример

Давайте воспользуемся методом теоремы косинусов, чтобы решить пример. У нас есть четырехугольник со сторонами a = 5, b = 7 и c = 9, а также углом C = 30 градусов. Мы хотим найти длину четвертой стороны.
Используя формулу теоремы косинусов, мы получаем:
c^2 = a^2 + b^2 — 2ab*cos(C)
c^2 = 5^2 + 7^2 — 2*5*7*cos(30)
c^2 = 25 + 49 — 70*cos(30)
c^2 = 74 — 70*0.866
c^2 = 74 — 60.82
c^2 = 13.18
c = sqrt(13.18)
c ≈ 3.63
Таким образом, длина четвертой стороны четырехугольника составляет около 3.63.
Мне интересно, как вы решаете подобные задачи? Вы пробовали использовать другие методы, или у вас есть свои собственные приемы? Дайте знать в комментариях!
Поиск дополнительных углов и сторон
Исследование четырехугольников может быть увлекательным и интересным процессом. Когда вам известны размеры трех сторон четырехугольника и одного из его углов, вы можете использовать различные методы для нахождения оставшихся сторон и углов.
1. Метод синусов и косинусов
Один из наиболее распространенных методов для нахождения дополнительных углов и сторон основан на использовании синусов и косинусов. Если у вас уже есть один угол и три стороны четырехугольника, вы можете использовать эти тригонометрические функции для нахождения остальных углов и сторон.
Например, если у вас есть четырехугольник ABCD, где известны стороны AB, BC, CD и угол B, вы можете использовать формулы синусов и косинусов для нахождения углов C, D и сторон AC, AD.
2. Теорема косинусов
Теорема косинусов позволяет находить длину одной стороны треугольника, если известны длины двух других сторон и угла между ними. В контексте поиска четвертой стороны четырехугольника, вы можете использовать теорему косинусов, чтобы найти длину одной из оставшихся сторон.
Например, если у вас уже есть четырехугольник ABCD, где известны стороны AB, BC, CD и углы B и C, вы можете использовать теорему косинусов для нахождения длины стороны AD.
3. Уравнения углов
Если известны длины всех четырех сторон четырехугольника и один угол, вы можете использовать уравнения углов, чтобы найти значения остальных углов. Уравнения углов представляют собой систему уравнений, в которых сумма углов четырехугольника равна 360 градусам.
Например, если у вас уже есть четырехугольник ABCD, где известны стороны AB, BC, CD, DA и угол B, вы можете составить систему уравнений на основе уравнений углов для нахождения значений углов A, C и D.
4. Таблица углов и сторон
Для облегчения поиска дополнительных углов и сторон можно использовать таблицу углов и сторон. В таблице указываются длины сторон и значения углов, а также описывается связь между ними.
| стороны | углы |
|---|---|
| AB, BC, CD, DA | A, B, C, D |
По этой таблице вы можете определить значения сторон и углов, если известны значения хотя бы трех сторон и одного угла.
Итак, используя методы синусов и косинусов, теорему косинусов, уравнения углов и таблицу углов и сторон, вы сможете легко находить дополнительные углы и стороны четырехугольника. Не бойтесь экспериментировать и применять различные методы в зависимости от ваших конкретных данных и задачи!
Поиск с использованием теоремы Пифагора
c2 = a2 + b2
Эта теорема может быть использована не только для нахождения длин сторон прямоугольного треугольника, но и для нахождения четвертой стороны четырёхугольника с известными сторонами.
Для решения задачи с использованием теоремы Пифагора необходимо знать длины трёх сторон четырёхугольника, а также знать, что четырёхугольник является прямоугольником. Если все эти условия выполняются, то можно приступить к решению.
- Определите, какие из сторон четырёхугольника являются диагоналями прямоугольника. Диагонали прямоугольника являются его сторонами и пересекаются в его вершине. Если диагонали известны, то их длины можно использовать для нахождения четвёртой стороны.
- Примените теорему Пифагора, чтобы найти длины сторон прямоугольного треугольника, образованного одной из диагоналей и одной из сторон четырёхугольника.
- При наличии длин двух сторон прямоугольного треугольника можно определить длину третьей стороны с помощью теоремы Пифагора.
Приведу пример для более наглядного объяснения. Представим, что у нас есть прямоугольный четырёхугольник ABCD, где стороны AB и BC являются параллельными и равными диагоналями. Нам известны длины сторон AB, BC и CD, а мы хотим найти длину четвёртой стороны AD.
Сначала мы находим длины сторон AB и BC с помощью формулы длины прямоугольной гипотенузы (c):
AB2 = CD2 + BC2
BC2 = AB2 — CD2
Затем, используя теорему Пифагора, находим длину стороны AD:
AD2 = AB2 + CD2
AD = √(AB2 + CD2)
Таким образом, мы можем найти длину четвёртой стороны четырёхугольника, используя теорему Пифагора.
| Страница | Ссылка |
|---|---|
| Википедия | https://ru.wikipedia.org/wiki/Теорема_Пифагора |
| MathIsFun | https://www.mathsisfun.com/geometry/pythagorean-theorem.html |
Применение формулы косинусов
c^2 = a^2 + b^2 — 2ab * cos(C)
Где «c» — третья сторона треугольника, «a» и «b» — длины двух других сторон, «C» — угол между этими сторонами.
Формула косинусов является очень полезным инструментом для нахождения неизвестных сторон треугольника, когда даны длины двух других сторон и угол между ними. Она особенно полезна при решении задач геометрии и физики, таких как определение расстояния между двумя объектами или нахождение длины пути, пройденного объектом.
Давайте рассмотрим пример применения формулы косинусов:
Предположим, у нас есть треугольник ABC, в котором известны длины двух сторон и угол между ними:
Длина стороны AB = 5 см
Длина стороны BC = 7 см
Угол ACB = 60 градусов
Мы хотим найти длину стороны AC. Мы можем использовать формулу косинусов для решения этой задачи:
c^2 = a^2 + b^2 — 2ab * cos(C)
AC^2 = AB^2 + BC^2 — 2 * AB * BC * cos(ACB)
AC^2 = 5^2 + 7^2 — 2 * 5 * 7 * cos(60)
AC^2 = 25 + 49 — 70 * cos(60)
AC^2 = 74 — 70 * 0.5
AC^2 = 74 — 35
AC^2 = 39
AC ≈ √39
AC ≈ 6.24 см
Таким образом, длина стороны AC примерно равна 6.24 см.
Как вы видите, формула косинусов позволяет нам находить неизвестные стороны треугольника, основываясь на длинах других сторон и угле между ними. Это очень полезный инструмент для решения задач геометрии и физики.
Использование формулы Герона
Суть формулы Герона заключается в использовании разложения четырехугольника на два треугольника и применении теоремы косинусов для нахождения четвертой стороны. Формула применима для четырехугольников произвольной формы, не обязательно выпуклых.
Процедура нахождения четвертой стороны четырехугольника по формуле Герона может быть представлена следующим образом:
- Найдите длины трех известных сторон четырехугольника.
- Найдите один из углов четырехугольника.
- Разложите четырехугольник на два треугольника, используя известные стороны и найденный угол.
- Примените теорему косинусов для нахождения длины четвертой стороны каждого из двух треугольников.
- Сложите полученные значения длин четвертых сторон и найдите итоговую длину четвертой стороны четырехугольника.
Применение формулы Герона может быть полезно при решении задач пометкой о нахождении длины четвертой стороны четырехугольника, особенно когда известны длины трех других сторон.
Найти четвертую сторону четырехугольника может быть проблематично, но благодаря формуле Герона это становится проще. Использование этого метода позволяет быстро и точно определить длину четвертой стороны четырехугольника, что делает его очень удобным и эффективным инструментом при работе с геометрическими фигурами.






