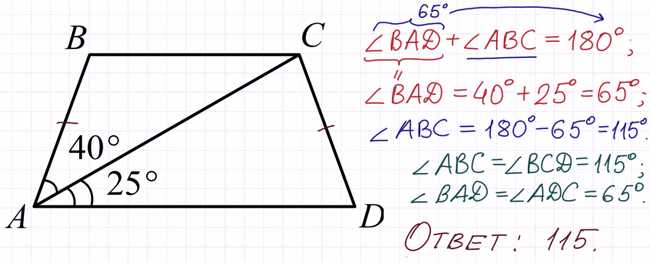
Когда речь идет о равнобедренной трапеции ABCD с диагональю AC, важно знать, как найти больший угол. Существует несколько способов решить эту задачу, которые мы рассмотрим.
1. Использование теоремы косинусов: можно найти длины всех сторон трапеции и применить формулу косинусов для нахождения угла.
2. Разделение трапеции на два прямоугольных треугольника: это позволяет использовать теорему Пифагора для нахождения длин сторон и далее применять тригонометрические функции.
3. Использование свойств параллельных линий: находим соответствующие углы, используя свойства параллельных и пересекающихся прямых.
4. Использование связи углов трапеции: зная, что сумма всех углов равна 360 градусов, можно выразить один из углов через остальные и найти больший угол.
5. Помощь компьютерных программ: существуют специализированные программы, которые могут найти углы трапеции за вас.
Способ 1: Использование базовой геометрии
Когда речь заходит о нахождении большего угла равнобедренной трапеции, на помощь приходит базовая геометрия. Давайте посмотрим, как мы можем использовать эти знания для решения этой задачи.
В равнобедренной трапеции, два угла основания (A и B) и два угла боковых сторон (C и D) суммируются до 180 градусов. Нам дано, что диагональ AC имеет длину 5 единиц.
Пусть угол A – это угол при вершине A трапеции, угол B – угол при вершине B. Чтобы найти больший угол, мы должны понять, какой из углов, A или B, больше.
Так как трапеция равнобедренная, основания трапеции, стороны AB и CD, равны друг другу. Это означает, что углы A и B также равны. Но какой из них больше?
Чтобы ответить на этот вопрос, давайте рассмотрим треугольники ABC и BCD. Они равнобедренные, поэтому у них совпадают некоторые стороны и углы.
В треугольнике ABC у нас есть угол C, который равен углу D в треугольнике BCD. Кроме того, сторона AC имеет длину 5 единиц.
Теперь представьте, что мы прикладываем основание BC треугольника BCD к основанию АС треугольника ABC. Поскольку углы C и D равны, сторона BC совмещается с частью стороны AC, и мы получаем треугольник ABD.
Таким образом, углы A и B в треугольнике ABD являются одинаковыми (равными углам A и B в трапеции ABC) и составляют половину угла C или D в треугольнике ABC или BCD.
Так как углы C и D суммируются до 180 градусов, каждый из этих углов равен 90 градусам. Значит, углы A и B в трапеции ABC также равны 90 градусам.
Теперь у нас есть два прямых угла в трапеции ABC. Чтобы найти больший угол, нам нужно знать, на какую сторону они направлены.
Итак, чтобы найти больший угол A или B, мы должны ориентироваться на боковую сторону, к которой он направлен. Если боковая сторона справа от диагонали AC, то больший угол будет A. Если боковая сторона слева от диагонали AC, то больший угол будет B.
Вот и весь способ 1 использования базовой геометрии для нахождения большего угла равнобедренной трапеции. Надеюсь, это помогло вам лучше понять эту задачу и решить ее. В следующем способе мы рассмотрим другой подход к решению этой задачи.
Шаг 1: Найдите угол между основанием и боковой стороной

Перед тем, как найти больший угол, нужно определить, какие углы мы имеем в виду. Равнобедренная трапеция имеет две параллельные основания и две равных боковые стороны. Угол между одним из оснований и боковой стороной называется базовым углом.
Для нахождения большего базового угла вам понадобится знание о сумме углов треугольника. В данном случае, базовый угол и два угла при основаниях образуют треугольник.
Чтобы найти больший угол, нужно узнать, какие углы в вашей трапеции уже известны и сколько они составляют в сумме. Затем вычитаем эту сумму из 180 градусов (сумма углов треугольника), и получаем величину, на сколько можно увеличить базовый угол, чтобы получить больший угол.
- 1. Определите известные углы в вашей трапеции.
- 2. Сложите их и найдите сумму.
- 3. Вычтите сумму из 180 градусов.
- 4. Полученную разницу добавьте к базовому углу, чтобы найти больший угол.
Например, если известно, что базовый угол равен 60 градусов, а сумма углов при основаниях равна 100 градусам, то разница составит 180 — 100 = 80 градусов. Добавив эту разницу к базовому углу, мы получим больший угол, равный 60 + 80 = 140 градусов.
Помните, что это только один из способов найти больший угол в равнобедренной трапеции. В зависимости от известных данных, может понадобиться использовать другие методы. Но, я уверен, что с помощью этого шага вы научитесь находить больший угол с легкостью!
Шаг 2: Используйте свойство равнобедренности

Свойство равнобедренной трапеции гласит, что основания равны, а боковые стороны равны. Воспользуемся этим свойством для нахождения большего угла трапеции ABCD.
Предположим, что основаниям AB и CD соответствуют стороны a, а боковым сторонам BC и AD — стороны b. Также предположим, что угол между сторонами a и b составляет Х градусов.
Используя свойство равнобедренности, мы можем сказать, что углы между сторонами a и боковыми сторонами BC и AD также равны Х градусов каждый.
Поскольку сумма углов в треугольнике равна 180 градусам, мы можем записать следующее уравнение:
Х + Х + угол B + угол D = 180 градусов
Учитывая, что угол B и угол D являются вершинными углами трапеции, они равны. Отсюда следует, что:
2Х + 2х = 180 градусов
Решив это уравнение, мы найдем значение угла Х. После установления значения угла Х, мы можем найти значение большего угла трапеции исходя из следующего уравнения:
Больший угол = Х + угол B или угол D
Подставив значение угла Х, мы можем получить искомую величину большего угла трапеции.
Таким образом, используя свойство равнобедренности, мы сможем найти больший угол равнобедренной трапеции ABCD с диагональю AC.
Способ 2: Использование теоремы косинусов
Если вы ищете способ найти больший угол равнобедренной трапеции ABCD с диагональю AC, то использование теоремы косинусов может быть очень полезным.
Теорема косинусов гласит, что в треугольнике сторона в квадрате равна сумме квадратов двух других сторон, умноженной на два и умноженной на косинус угла между этими сторонами:
c^2 = a^2 + b^2 — 2ab·cos(C)
где c — третья сторона, a и b — две другие стороны, C — угол между этими двумя сторонами.
В нашем случае, мы знаем, что стороны AB и CD равны, так как трапеция равнобедренная. Поэтому мы можем использовать эту формулу для нахождения угла ACD.
AC^2 = AD^2 + CD^2 — 2·AD·CD·cos(ACD)
Если мы хотим найти больший угол, то нужно найти значение угла ACD, которое превышает 180 градусов. Для этого нам надо найти значение косинуса угла ACD.
Умножив данное уравнение на 2 и переписав его в виде:
2·AC·CD·cos(ACD) = AD^2 + CD^2 — AC^2
Мы можем находить значение косинуса угла ACD и сравнивать его с -1 и 1, чтобы определить, является ли угол ACD острым (-1 < cos(ACD) < 1) или тупым (cos(ACD) = -1 или cos(ACD) = 1).
Если угол ACD оказывается острым, то мы можем найти значение самого угла ACD, используя обратную функцию cos(cos^-1). Затем мы можем сравнить найденное значение угла с другими углами трапеции и найти наибольший из них.
Итак, использование теоремы косинусов дает нам возможность определить, какой из углов равнобедренной трапеции ABCD с диагональю AC является наибольшим. Этот метод может быть полезен, когда мы хотим найти больший угол, а также исследовать свойства геометрических фигур.
Шаг 1: Найдите длины сторон трапеции
Перед тем, как начать поиск большего угла равнобедренной трапеции ABCD с диагональю AC, важно определить длины ее сторон. Зная эти значения, мы сможем продолжить наше исследование и найти больший угол трапеции.
Давайте взглянем на обычную равнобедренную трапецию ABCD:
- AB и CD — параллельные стороны трапеции, называемые основаниями;
- BC и AD — неравные боковые стороны;
- AC и BD — диагонали, которые пересекаются в точке O.
Для нахождения длин сторон трапеции можно воспользоваться различными методами:
- Используйте известные значения. Если вам уже известны длины сторон или углы трапеции, вы можете использовать их для расчета других параметров. Например, если вам дана длина одной из сторон, вы можете использовать формулу для расчета периметра трапеции или длин двух других сторон.
- Используйте геометрические свойства. Зная, что трапеция имеет две параллельные стороны и две равные углы, вы можете использовать геометрические свойства треугольников для нахождения длин сторон. Например, вы можете разделить трапецию на два треугольника и использовать теорему Пифагора или теорему косинусов для нахождения длин сторон этих треугольников.
- Используйте специальные формулы. Для равнобедренной трапеции с диагональю AC существуют специальные формулы для нахождения длин сторон. Например, вы можете использовать формулу для нахождения диагонали трапеции через длины оснований и угол между ними.
Выберите наиболее удобный для вас метод и найдите длины сторон трапеции ABCD. Затем переходите к следующему шагу, чтобы найти больший угол равнобедренной трапеции.
Шаг 2: Примените теорему косинусов
Теорема косинусов гласит, что в треугольнике сторона в квадрате равна сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В нашем случае, сторона AC является диагональю трапеции, а стороны AD и BC — основаниями. Пусть хотя бы одно основание трапеции, например AD, равно a, а угол DAC равен α.
Применим теорему косинусов к треугольнику DAC:
- Сторона AC в квадрате равна сумме квадратов сторон AD и DC минус удвоенное произведение этих сторон на косинус угла α.
- AC² = AD² + DC² — 2 * AD * DC * cos(α).
Аналогичное равенство можно записать для треугольника DBC:
- AC² = BC² + DC² — 2 * BC * DC * cos(α).
Оба выражения равны между собой, так как сторона AC общая для обоих треугольников. Поэтому можно записать:
- AD² + DC² — 2 * AD * DC * cos(α) = BC² + DC² — 2 * BC * DC * cos(α).
Теперь перенесём все слагаемые, содержащие cos(α), на одну сторону уравнения:
- AD² — BC² = 2 * AD * DC * cos(α) — 2 * BC * DC * cos(α).
Факторизуем cos(α) из обеих частей уравнения:
- AD² — BC² = (2 * AD * DC — 2 * BC * DC) * cos(α).
- AD² — BC² = 2 * DC * (AD — BC) * cos(α).
Теперь можно выразить cos(α) через известные величины:
- cos(α) = (AD² — BC²) / (2 * DC * (AD — BC)).
Таким образом, мы получили выражение для cos(α), которое позволит нам вычислить значение угла α. Проделаем аналогичные шаги для угла DBC, и вычислим больший из двух углов нашей равнобедренной трапеции. А дальше… что ты думаешь, читатель? Как мы продолжим наше увлекательное путешествие по поиску большего угла трапеции? Подсказка: мы уже сделали два шага из пяти!
Способ 3: Использование свойств смежных углов
Для использования этого способа необходимо знать, что углы, образованные диагоналями и боковыми сторонами равнобедренной трапеции, являются смежными.
Итак, для нахождения большего угла в равнобедренной трапеции ABCD с диагональю AC, можно использовать следующий алгоритм:
- Найдите все смежные углы, образованные диагоналями и боковыми сторонами равнобедренной трапеции.
- Сравните значения этих углов и определите наибольший из них. Это и будет больший угол равнобедренной трапеции.
Использование свойств смежных углов — простой и эффективный способ определить больший угол равнобедренной трапеции с диагональю AC. Он основан на особенностях геометрических фигур и может быть использован при решении различных задач.






