
Когда речь идет о решении геометрических задач, поиск большего основания трапеции может быть вызовом. Однако справиться с этой задачей несложно, если знаешь правильный подход. В этом пошаговом руководстве мы рассмотрим, как найти большее основание трапеции, используя среднюю линию и меньшую сторону.
В процессе решения задачи мы будем использовать базовые геометрические принципы и формулы для трапеции. Это позволит нам точно определить положение и размеры каждого элемента фигуры и, в итоге, найти большее основание трапеции. Следуя этому пошаговому руководству, ты сможешь смело решать подобные задачи и углубить свои знания геометрии. Приступим к изучению метода поиска большего основания трапеции!
Шаг 1: Задача и известные данные
Добро пожаловать к нам в увлекательный мир математики! Сегодня мы рассмотрим небольшую задачу о трапеции. Возможно, ты уже сталкивался с этой фигурой на уроках, но сейчас мы пойдем немного глубже и рассмотрим, как можно найти большее основание трапеции, если нам известны только средняя линия и меньшая сторона.
Представь себе, что у тебя есть трапеция с двумя параллельными основаниями. Одно из этих оснований называется большим, а другое — малым. В центре трапеции проведена средняя линия, которая соединяет середины двух оснований. Также у тебя есть информация о длине меньшей стороны трапеции и о длине средней линии.
Теперь вопрос: как найти длину большего основания трапеции, зная только среднюю линию и меньшую сторону? Давай вместе рассмотрим решение этой задачи!
Шаг 2: Описание формулы для нахождения большего основания
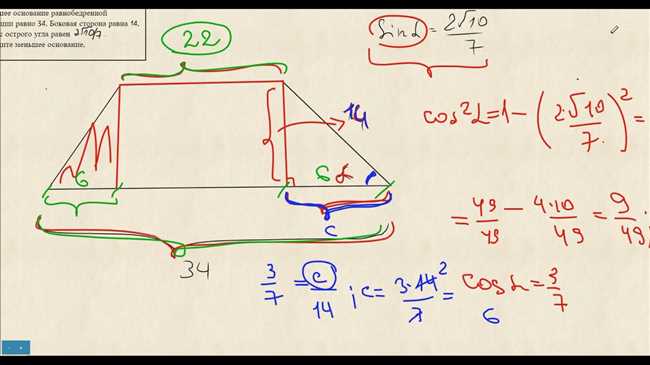
Формула для нахождения большего основания:
Большее основание = 2 x средняя линия — меньшая сторона
Давайте разберемся, что означает каждая часть этой формулы. Средняя линия обозначена как «средняя линия», а меньшая сторона как «меньшая сторона». Формула говорит нам, что мы должны умножить среднюю линию на 2 и вычесть из этого результата длину меньшей стороны, чтобы найти длину большего основания.
Но почему мы используем именно такую формулу? Все дело в теореме Талеса, которая гласит, что если у нас есть три параллельные прямые линии, то отношение длин отрезков, образованных пересечениями этих линий, будет одинаковым. В нашем случае, средняя линия и большее основание являются параллельными линиями, поэтому мы можем использовать теорему Талеса для определения длины большего основания.
Используя эту формулу, мы сможем точно вычислить длину большего основания трапеции на основе известных величин, таких как средняя линия и меньшая сторона. Таким образом, шаг за шагом мы приближаемся к решению задачи и нахождению большего основания нашей трапеции. Продолжим работу и перейдем к следующему шагу!
Шаг 3: Подстановка известных данных в формулу
Теперь, когда мы знаем среднюю линию и меньшую сторону трапеции, мы можем перейти к шагу, который позволит нам найти большее основание.
Формула для вычисления большего основания трапеции выглядит следующим образом:
B = 2M — m
Где:
B — большее основание трапеции;
M — средняя линия трапеции;
m — меньшая сторона трапеции.
Теперь давайте подставим известные нам значения и выполним вычисления. Предположим, что средняя линия трапеции равна 8 см, а меньшая сторона равна 5 см.
Подставим эти значения в формулу:
Большее основание, B = 2 * 8 — 5
Выполним вычисления:
B = 16 — 5
B = 11
Таким образом, большее основание трапеции составляет 11 см.
Теперь вы знаете, как найти большее основание трапеции с помощью средней линии и меньшей стороны. Это простая и эффективная формула, с которой легко работать. Попробуйте применить ее на практике и убедитесь, что она работает!
Шаг 4: Расчет большего основания
Допустим, что средняя линия равна a, а меньшая сторона равна b. Также пусть длина одной из боковых сторон трапеции будет равна c. Чтобы найти большее основание, мы воспользуемся следующей формулой:
Большее основание = 2 * a — b + 2 * c
В данной формуле мы добавляем два раза длину боковой стороны, поскольку она учитывается дважды – она является одной из сторон большего основания и служит в качестве границы для построения средней линии.
Теперь, применяя эту формулу к значениям средней линии и меньшей стороны, которые мы уже нашли, можем вычислить большее основание.
Давайте рассмотрим пример для наглядности. Предположим, что средняя линия равна 10 см, меньшая сторона – 5 см, а длина одной из боковых сторон – 8 см. Применяя формулу, получаем:
Большее основание = 2 * 10 — 5 + 2 * 8
Большее основание = 20 — 5 + 16
Большее основание = 31 см
Таким образом, большее основание трапеции равно 31 см.
Теперь у нас есть все необходимые значения для построения трапеции по средней линии и меньшей стороне. Продолжайте следовать инструкциям, чтобы завершить построение и наслаждаться результатом!
Шаг 5: Проверка полученного результата
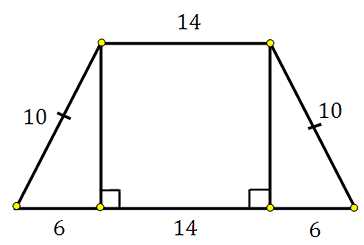
После выполнения всех предыдущих шагов, необходимо проверить корректность полученного результата. Это важный этап, который позволяет избежать ошибок и убедиться в правильности решения задачи.
Для этого можно использовать следующий алгоритм:
- Возьмите ранее найденное значение основания трапеции по средней линии.
- Умножьте это значение на 2.
- Вычтите из полученного результата значение меньшей стороны трапеции.
- Если полученное значение равно большей стороне трапеции (выражение верно), значит, ваш результат правильный.
- Если полученное значение не равно большей стороне трапеции (выражение неверно), значит, в процессе вычислений была допущена ошибка. Проверьте все предыдущие шаги и исправьте возможные ошибки.
Обратите внимание, что величина погрешности в вычислениях может присутствовать из-за округления чисел или незначительных ошибок в исходных данных. Если разница между полученным и ожидаемым значением несущественна, можно считать результат удовлетворительным.






