Как найти боковую сторону прямоугольной трапеции: полезные советы и формулы

Если у вас есть прямоугольная трапеция, то вы можете легко найти длину ее боковой стороны, если известны другие параметры. Существует несколько формул, которые помогут вам решить эту задачу. Одним из способов является использование теоремы Пифагора, которая устанавливает соотношение между длиной гипотенузы и катетов прямоугольного треугольника. Вы можете применить эту формулу к боковым сторонам прямоугольной трапеции, чтобы найти искомую длину. Кроме того, существуют и другие методы, например использование теоремы косинусов или формулы для нахождения площади трапеции. Необязательно запоминать все эти формулы, достаточно понимать принцип их работы, чтобы легко решать задачи с поиском боковых сторон прямоугольных трапеций.

Определение прямоугольной трапеции

Главная особенность прямоугольной трапеции заключается в том, что ее боковые стороны образуют прямой угол, то есть равны 90 градусам. Это делает возможным использование теорем Пифагора и тригонометрических функций для нахождения длины боковых сторон и других параметров.

Прямоугольные трапеции часто встречаются в различных объектах и конструкциях, таких как здания, мебель, упаковка и т.д. Благодаря своим уникальным свойствам, они позволяют создавать устойчивые и эстетически приятные конструкции.

Формулы для нахождения боковой стороны

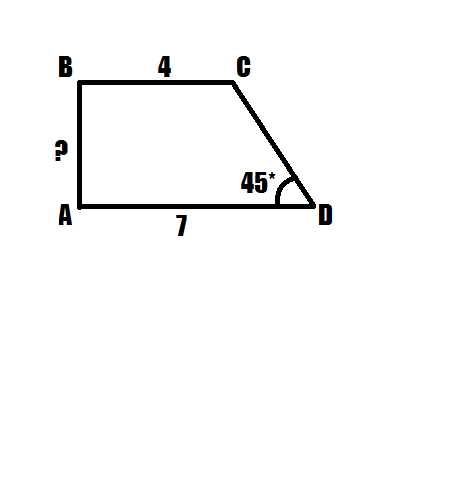
Если вы хотите узнать, как найти боковую сторону прямоугольной трапеции, у вас есть несколько вариантов. Здесь я расскажу вам о двух основных формулах, которые вам помогут с этой задачей.

1. Формула по основанию и высоте

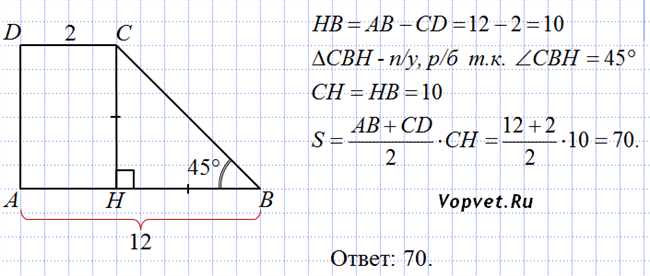
Первая формула основана на знании длины основания (большей стороны) и высоты трапеции. Она выглядит так:

Стoрoна = h * (a + b) / 2

Где:

• h — высота трапеции
• a и b — длины основных сторон трапеции

Таким образом, если у вас есть известные значения основания и высоты, вы можете легко вычислить боковую сторону.

2. Формула по углу и стороне

Вторая формула позволяет найти боковую сторону, зная длину одной из наклонных сторон и величину угла между этой стороной и одной из оснований. Вот эта формула:

Стoронa = a / sin(Угол)

Где:

• a — длина наклонной стороны
• Угол — величина угла между наклонной стороной и одной из оснований

Если у вас есть информация о длине стороны и угле, вы сможете легко вычислить боковую сторону.

Эти две формулы являются основными методами для нахождения боковой стороны прямоугольной трапеции. Используя одну из них, вы можете решить задачу с легкостью. Не забудьте проверить свои расчеты и убедиться в правильности ответа.

Полезные советы по нахождению боковой стороны прямоугольной трапеции

Если вы сталкиваетесь с задачей нахождения боковой стороны прямоугольной трапеции, то вам может быть полезно знать несколько советов, которые помогут вам решить эту задачу.

Перед тем как приступить к решению проблемы, важно вспомнить основные характеристики прямоугольной трапеции. Это четырехугольник, у которого две параллельные стороны и две прямые углы. Этот вид трапеции можно рассматривать как прямоугольник, у которого один угол обрезан. Именно этот угол нужно восстановить, чтобы найти боковую сторону.

Если вам известны длины оснований и высота прямоугольной трапеции, тогда вы можете использовать следующую формулу для нахождения боковой стороны:

Сторона = √((основание1 — основание2 + 2 * высота) * (основание1 + основание2 — 2 * высота))

Например, если основание1 равно 8, основание2 равно 4 и высота равна 6, то боковая сторона будет равна:

Сторона = √((8 — 4 + 2 * 6) * (8 + 4 — 2 * 6)) = √(16 * 12) = √192 ≈ 13.86

Еще один полезный совет — визуализируйте прямоугольную трапецию и обозначьте известные значения на диаграмме. Это поможет вам лучше понять задачу и найти оптимальный подход к ее решению.

Если вам известны боковая сторона и одно из оснований прямоугольной трапеции, тогда вы можете использовать следующую формулу для нахождения высоты:

Высота = √(боковая сторона² — (основание1 — основание2)²)

Например, если боковая сторона равна 10, основание1 равно 8 и основание2 равно 6, то высота будет равна:

Высота = √(10² — (8 — 6)²) = √(100 — 2²) = √(100 — 4) = √96 ≈ 9.80

Также не забывайте использовать некоторые свойства прямоугольных трапеций. Например, противолежащие углы прямоугольной трапеции смежны (сумма этих углов равна 180 градусам) и дополнительны (сумма этих углов равна 90 градусам).

Зная эти советы и используя соответствующие формулы, вы сможете справиться с задачей нахождения боковой стороны прямоугольной трапеции. Не бойтесь экспериментировать и искать альтернативные подходы — это поможет вам развить математическое мышление и научиться решать сложные задачи.

Примеры решения задач

Для лучшего понимания как найти боковую сторону прямоугольной трапеции, рассмотрим несколько примеров решения задач.

Пример 1:

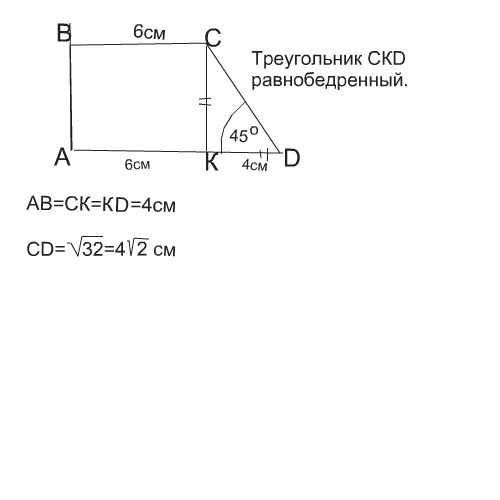
Дана прямоугольная трапеция ABCD, у которой основания AB и CD имеют длины 6 см и 10 см соответственно, а высота h равна 4 см. Нужно найти длину боковой стороны.

Для решения этой задачи воспользуемся теоремой Пифагора. По теореме, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В данном случае катетами являются сторона трапеции BC и высота h. Используя формулу, получим:

BC² = AB² — h²

Подставляем известные значения и вычисляем:

BC² = 6² — 4² = 36 — 16 = 20

Извлекаем квадратный корень и получаем:

BC = √20 ≈ 4.47 см

Таким образом, длина боковой стороны прямоугольной трапеции равна около 4.47 см.

Пример 2:

Дана прямоугольная трапеция XYZW, у которой основания XY и ZW имеют длины 12 см и 16 см соответственно, а углы прямые. Известно, что боковые стороны XY и ZW равны между собой. Нужно найти длину боковой стороны.

Для решения этой задачи можем воспользоваться подходом с использованием пропорции. Согласно свойству подобных прямоугольных трапеций, отношение длин боковых сторон равно отношению длин оснований. То есть:

XY/ZW = XY/XY — BC

Используя формулу и подставляя известные значения, выразим длину боковой стороны:

XY/16 = 12/12 — BC

Упрощаем выражение и решаем уравнение:

XY/16 = 1 — BC/12

XY/16 = 12/12 — BC/12

XY/16 = 1 — BC/12

BC/12 = 1 — XY/16

BC/12 = (16 — XY)/16

BC = (16 — XY)/16 * 12

Подставляем известные значения и вычисляем:

BC = (16 — 12)/16 * 12 = 4/16 * 12 = 3 см

Таким образом, длина боковой стороны прямоугольной трапеции равна 3 см.

Теперь, после рассмотрения этих примеров, вы сможете легко решать задачи, связанные с нахождением боковой стороны прямоугольных трапеций.