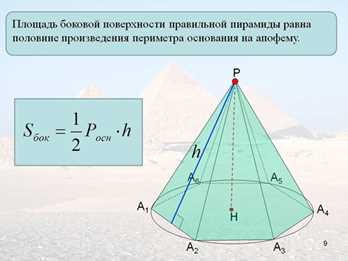
Формула нахождения боковой стороны правильной четырехугольной пирамиды с высотой 8 является довольно простой и проводится посредством применения теоремы Пифагора. Для расчета необходимо знать основания пирамиды. Боковая сторона представляет собой ребро пирамиды, которое соединяет ее вершину с одним из ее оснований. Используя теорему Пифагора, мы можем выразить боковую сторону через основание и высоту пирамиды. Для этого нужно возвести основание в квадрат, затем вычесть квадрат высоты и извлечь корень из полученной разности. Таким образом, формула выглядит следующим образом: боковая сторона = √(основание^2 — высота^2). С использованием этой формулы вы сможете точно определить длину боковой стороны пирамиды.
Что такое правильная четырехугольная пирамида?

Правильная четырехугольная пирамида имеет несколько характеристик, которые делают ее уникальной.
1. Симметрия:
Все боковые грани правильной четырехугольной пирамиды равны между собой, что создает симметричную структуру. Это означает, что пирамида выглядит одинаково со всех сторон и может вращаться вокруг своей вершины, не изменяя своей формы.
2. Стабильность:
Правильная четырехугольная пирамида обладает высокой стабильностью, благодаря равновесию сил, действующих на нее. Это связано с равенством длин боковых сторон, что позволяет пирамиде сохранять свою форму даже под воздействием внешних факторов.
3. Универсальность:
Правильная четырехугольная пирамида является одной из самых распространенных форм в природе и в архитектуре. Ее простая структура позволяет использовать пирамиду в различных областях, таких как строительство, дизайн, искусство и даже в научных исследованиях.
Итак, правильная четырехугольная пирамида — это геометрическое тело, которое обладает симметрией, стабильностью и универсальностью. Это уникальная форма, которая встречается повсюду в нашем мире и привлекает наше внимание своей простотой и элегантностью.
Как найти боковую сторону такой пирамиды?
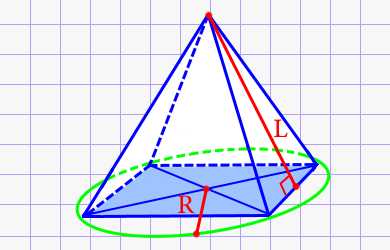
Если у вас есть правильная четырехугольная пирамида с высотой 8, и вы хотите найти ее боковую сторону, есть специальная формула, которую можно использовать. Эта формула основана на теории прямоугольных треугольников и позволяет точно вычислить боковую сторону пирамиды. Хотите узнать больше?
- Первым шагом необходимо разделить пирамиду на два прямоугольных треугольника. Для этого проведите линию, соединяющую вершину пирамиды с серединой основания. Получатся два треугольника, каждый из которых будет иметь высоту 8 и одну из сторон основания пирамиды как гипотенузу.
- Далее используйте теорему Пифагора для нахождения длины одной из сторон основания пирамиды. Теорема Пифагора гласит, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы. В нашем случае, одна из сторон основания будет являться гипотенузой, а высота пирамиды — катетом. Таким образом, по формуле a^2 + 8^2 = b^2 (где a — боковая сторона пирамиды, b — диагональ основания пирамиды) можно найти длину боковой стороны.
- Решив уравнение и найдя значение длины диагонали, подставьте его обратно в формулу и найдите длину боковой стороны пирамиды. Просто возведите длину диагонали в квадрат и отнимите 64 (поскольку 8^2 равно 64).
Теперь вы знаете, как найти длину боковой стороны правильной четырехугольной пирамиды с высотой 8. Не забывайте использовать теорему Пифагора и формулу, описанную выше, чтобы получить точный результат. Удачи в расчетах и построении!
Пример применения формулы
Боковая сторона = (2 * высота) / √3
Эта формула основывается на геометрических свойствах правильной четырехугольной пирамиды и позволяет нам легко и быстро находить значение боковой стороны при заданной высоте.
Рассмотрим, например, пирамиду с высотой 8. Подставив это значение в нашу формулу, мы получим:
Боковая сторона = (2 *  / √3 ≈ 9.237
/ √3 ≈ 9.237
Таким образом, боковая сторона данной пирамиды составляет примерно 9.237 единиц длины.
Использование данной формулы позволяет нам упростить вычисления и получить быстрый результат при нахождении боковой стороны правильной четырехугольной пирамиды с заданной высотой. Это особенно полезно при проектировании строений или в задачах, связанных с геометрией и физикой.






