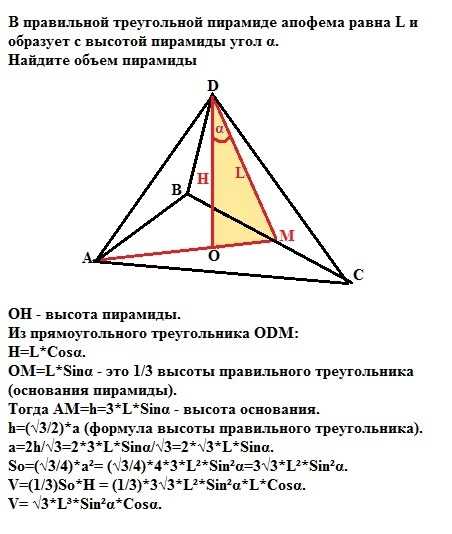
Как найти апофему в правильной треугольной пирамиде: подробное руководство
Хотите узнать, как найти апофему в правильной треугольной пирамиде? Не волнуйтесь, мы здесь, чтобы помочь вам! В данной статье мы расскажем вам о том, что такое апофема и как ее найти в таком геометрическом теле, как треугольная пирамида. Апофема — это линия, проведенная от вершины пирамиды до середины одной из ее боковых сторон. На самом деле, это довольно просто: вам понадобится только знание некоторых математических формул и немного времени. Мы подготовили для вас подробное руководство, которое поможет вам успешно найти апофему в правильной треугольной пирамиде. Начнем!
Что такое апофема и зачем она нужна
Зачем же нам нужна апофема? Она играет важную роль во многих вычислениях и формулах, связанных с правильными треугольными пирамидами. Помимо этого, апофема может использоваться для измерения высоты пирамиды.
Представь себе, что ты работаешь на стройке и должен построить правильную треугольную пирамиду. Как узнать ее высоту? Самый простой способ – измерить апофему. Зная длину апофемы и площадь основания, мы можем легко вычислить высоту пирамиды с помощью специальной формулы.
Кстати, апофема также позволяет узнать площадь лицевой поверхности пирамиды. Так как уравнение площади поверхности пирамиды включает апофему, зная ее значение, мы можем сразу вычислить этот параметр. Это очень удобно и экономит время при решении задач связанных с пирамидами.
Помимо вычислительной функции, апофема также имеет эстетическое значение. Она вносит гармонию и симметрию в пропорции пирамиды. Благодаря апофеме пирамида выглядит сбалансированной и красивой.
Известные значения апофемы в прямоугольной треугольной пирамиде
Чтобы вычислить апофему в прямоугольной треугольной пирамиде, нам необходимо знать длины сторон треугольника основания и высоту пирамиды.
Давайте представим, что у нас есть прямоугольная треугольная пирамида с основанием 3-4-5 и высотой 6. Чтобы найти апофему, нам необходимо поделить площадь основания на половину периметра основания:
Апофема = Площадь основания / Полу-периметр основания
Так как основание у нас является прямоугольным треугольником, его площадь можно найти по формуле:
Площадь = (периметр / 2) * радиус вписанной окружности
В данном случае радиус вписанной окружности будет равен половине гипотенузы, то есть 5 / 2 = 2.5. А периметр равен сумме длин сторон треугольника, то есть 3 + 4 + 5 = 12. Таким образом, площадь основания равна (12 / 2) * 2.5 = 15.
Теперь нужно найти полу-периметр основания, который равен половине суммы длин сторон треугольника, то есть (3 + 4 + 5) / 2 = 6. Следовательно, апофема равна 15 / 6 = 2.5.
Таким образом, в прямоугольной треугольной пирамиде с основанием 3-4-5 и высотой 6 известное значение апофемы составляет 2.5.
Формула для нахождения апофемы в произвольной треугольной пирамиде
Для расчета апофемы в произвольной треугольной пирамиде нужно знать длину стороны основания и угол между боковой гранью и основанием, который называется углом наклона (θ). Давайте представим, что сторона основания равна a, а угол наклона равен α.
Теперь, когда у нас есть эти данные, мы можем использовать формулу для нахождения апофемы:
Апофема = a x sin(α)
Итак, чтобы рассчитать апофему в произвольной треугольной пирамиде, умножьте длину стороны основания на синус угла наклона.
Однако обратите внимание, что в данной формуле длина стороны основания должна быть в радианах (или может быть преобразована в радианы), а угол наклона должен быть в градусах. Если вы имеете значения в других единицах измерения, обязательно убедитесь, что привели их к нужному формату перед применением данной формулы.
Я надеюсь, что эта формула поможет вам рассчитать апофему в произвольной треугольной пирамиде. Если у вас остались вопросы или вам нужна дополнительная информация, не стесняйтесь задавать их.
Пример расчета апофемы в треугольной пирамиде
Для расчета апофемы в треугольной пирамиде мы можем воспользоваться формулой:
a = √(h^2 + (a/2)^2)
Где:
- a — апофема
- h — высота треугольной пирамиды
- a/2 — половина стороны основания треугольной пирамиды
Допустим, у нас есть треугольная пирамида с высотой h = 10 и длиной стороны основания a = 6
Расчет апофемы будет следующим:
a = √((10^2) + (6/2)^2)
a = √(100 + 9)
a = √109
a ≈ 10.44
Таким образом, апофема треугольной пирамиды с высотой 10 и длиной стороны основания 6 равна приблизительно 10.44.
Какой результат мы получили! Апофема является важным параметром в треугольных пирамидах, так как она помогает нам понять, как далеко находится вершина от основания. Этот пример поможет вам лучше понять, как рассчитать апофему и использовать эту информацию в своих проектах или научных исследованиях.
Практическое применение апофемы в строительстве и геометрии
В строительстве апофема используется для определения высоты или глубины различных конструкций. Например, в треугольных пирамидах апофема может служить для вычисления высоты самой пирамиды или высоты ее боковой грани. Это особенно полезно при проектировании зданий, где точное определение размеров и высот является критическим.
В геометрии апофема часто используется для вычисления площадей и объемов различных геометрических фигур. Например, при нахождении площади или объема правильных многогранников, апофема играет важную роль. Она помогает определить расстояние от центра фигуры до ее граней, что в свою очередь является ключевым параметром при вычислении этих характеристик.
Также апофема находит применение в строительстве при проектировании сценических конструкций. Например, апофема может использоваться для определения высоты и глубины специальных эллиптических куполов или сооружений с закругленными формами. Благодаря точному определению размеров с использованием апофемы, строители могут создавать более сложные и эстетически привлекательные конструкции.






